【阅读笔记】Improved Training of Wasserstein GANs
Improved Training of Wasserstein GANs
Gulrajani I, Ahmed F, Arjovsky M, et al. Improved training of wasserstein gans[C]//Advances in Neural Information Processing Systems. 2017: 5767-5777.
GitHub: https://github.com/igul222/improved_wgan_training
Abstract
GAN虽然是个强有力的生成模型,但是训练不稳定的缺点影响它的使用。刚刚提出的 Wasserstein GAN (WGAN) 使得 GAN 的训练变得稳定,但是有时也会产生很差的样本和不收敛。我们发现这些问题的原因常常是因为 weight clipping 来满足 判别器(critic,os.坑,研究了半天才领会这个意思)的 Lipschitz constraint。我们把 weight clipping 转化为成 判别器 的梯度范数关于输入的惩罚。我们的方法优于 standard WGAN 和大部分的 GAN 的变种。
Introduction
Generative adversarial networks
Formally, the game between the generator G and the discriminator D is the minimax objective:
m i n G m a x D E x ∼ p r [ l o g D ( x ) ] + E x ^ ∼ p g [ l o g ( 1 − D ( x ^ ) ) ] min_Gmax_DE_{x\sim p_r}[logD(x)]+E_{\hat{x}\sim p_g}[log(1-D(\hat{x}))] minGmaxDEx∼pr[logD(x)]+Ex^∼pg[log(1−D(x^))]
In practice, the generator is instead trained to maximize E x ^ ∼ p g [ l o g ( D ( x ^ ) ) ] E_{\hat{x}\sim p_g}[log(D(\hat{x}))] Ex^∼pg[log(D(x^))]。因为这样可以规避当判别器饱和时的梯度消失。
Wasserstein GANs
The WGAN value function is constructed using the Kantorovich-Rubinstein duality to obtain
m i n G m a x D ∈ D E x ∼ p r [ D ( x ) ] − E x ^ ∼ p g [ D ( x ^ ) ] min_Gmax_{D\in\mathscr{D}}E_{x\sim p_r}[D(x)]-E_{\hat{x}\sim p_g}[D(\hat{x})] minGmaxD∈DEx∼pr[D(x)]−Ex^∼pg[D(x^)]
其中 D \mathscr{D} D是 1-Lipschitz functions。为了使判别器满足 k-Lipschitz 限制,需要将权重固定在 [ − c , c ] [-c,c] [−c,c],k是由 c c c和模型结构所决定。
Difficulties with weight constraints
如下图所示,发现进行 weight clipping 有两个特点,一是会使得权重集中在所设范围的两端,二是会很容易造成梯度爆炸或梯度消失。这是因为判别器要满足 Lipschitz 条件,但是判别器的目标是使得真假样本判别时差别越大越好,经过训练后,权值的绝对值就集中在最大值附近了。

Gradient penalty
Algorithm 1 WGAN with gradient penalty. We use default values of λ = 10 \lambda=10 λ=10, n c r i t i c = 5 n_{critic}=5 ncritic=5, KaTeX parse error: Expected 'EOF', got '\apha' at position 1: \̲a̲p̲h̲a̲=0.0001, β 1 = 0 \beta_1=0 β1=0, β 2 = 0.9 \beta_2=0.9 β2=0.9.
Require: The gradient penalty coefficient λ \lambda λ, the number of critic iterations per generator iteration n c r i t i c n_critic ncritic, the batch size m m m, Adam hyperparameters α , β 1 , β 2 \alpha,\beta_1,\beta_2 α,β1,β2.
Require: initial critic parameters w 0 w_0 w0, initial generator parameters θ 0 \theta_0 θ0.
- while θ \theta θ has not converged do
- for t = 1 , . . . , n c r i t i c t=1, ..., n_{critic} t=1,...,ncritic do
- for i = 1 , . . . , m i = 1, ..., m i=1,...,m do
- Sample real data x ∼ P r x\sim P_r x∼Pr, latent variable z ∼ p ( z ) z\sim p(z) z∼p(z), a random number ϵ ∼ U [ 0 , 1 ] \epsilon\sim U[0, 1] ϵ∼U[0,1].
- x ~ ← G θ ( z ) \tilde{x}\leftarrow G_{\theta}(z) x~←Gθ(z)
- x ^ ← ϵ x + ( 1 − ϵ ) x ^ \hat{x}\leftarrow\epsilon x + (1 −\epsilon)\hat{x} x^←ϵx+(1−ϵ)x^
- L ( i ) ← D w ( x ) − D w ( x ~ ) + λ ( ∣ ∣ ∇ x ^ D w ( x ^ ) ∣ ∣ 2 − 1 ) 2 L^{(i)}\leftarrow D_w(x) − D_w(\tilde{x}) + \lambda(||\nabla_{\hat{x}}D_w(\hat{x})||_2-1)^2 L(i)←Dw(x)−Dw(x~)+λ(∣∣∇x^Dw(x^)∣∣2−1)2
- end for
- w ← A d a m ( ∇ w 1 m ∑ i = 1 m L ( i ) , w , α , β 1 , β 2 ) w\leftarrow Adam(\nabla_w\frac{1}{m}\sum_{i=1}^mL^(i), w, \alpha, \beta_1, \beta_2) w←Adam(∇wm1∑i=1mL(i),w,α,β1,β2)
- end for
- Sample a batch of latent variables { z ( i ) } i = 1 m ∼ p ( z ) \{z^{(i)}\}^m_{i=1}\sim p(z) {z(i)}i=1m∼p(z).
- θ ← A d a m ( ∇ θ 1 m ∑ I = 1 m − D w ( G t h e t a ( z ) ) , θ , α , β 1 , β 2 ) \theta\leftarrow Adam(\nabla_{\theta}\frac{1}{m}\sum_{I=1}^m−D_w(G_{theta}(z)), θ, \alpha, \beta_1, \beta_2) θ←Adam(∇θm1∑I=1m−Dw(Gtheta(z)),θ,α,β1,β2)
- end while
WGAN-GP 的创新点在与优化了代价函数
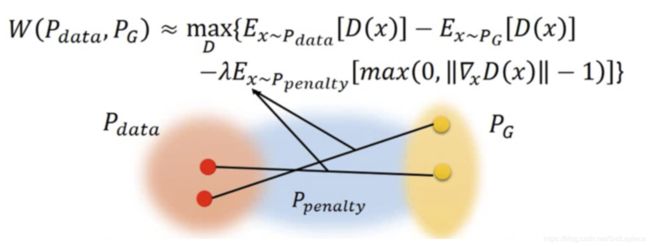
L = E x ∼ p r D w ( x ) − E x ∼ p g [ D w ( x ~ ) ] + λ E x ^ ∼ p x ^ [ ∣ ∣ ∇ x ^ D w ( x ^ ) ∣ ∣ 2 − 1 ) 2 ] L= E_{x\sim p_r}D_w(x) − E_{x\sim p_g}[D_w(\tilde{x})] + \lambda E_{\hat{x}\sim p_{\hat{x}}}[||\nabla_{\hat{x}}D_w(\hat{x})||_2-1)^2] L=Ex∼prDw(x)−Ex∼pg[Dw(x~)]+λEx^∼px^[∣∣∇x^Dw(x^)∣∣2−1)2]
对权重增加惩罚项,使得在原始数据和生成数据中间地带的权重的尽量小,相当于把 WGAN 的硬阈值转化为了软阈值。
Experiments
Conclusion
从实验上来看效果好于其他 GAN 方法,但是看其他资料说不一定好于WGAN,以后有空实验一下看看效果。
