机器学习之深入理解主成分分析（Principal Component Analysis）

引言

主成分分析（Principal Component Analysis，PCA），是一种常用的数据分析手段。对于一组不同维度之间可能存在线性相关关系的数据，PCA 能够把这组数据通过正交变换，变成各个维度之间线性无关的数据。经过 PCA 处理的数据中的各个样本之间的关系往往更直观，所以它是一种非常常用的数据分析和预处理工具。PCA 处理之后的数据各个维度之间是线性无关的，通过剔除方差较小的那些维度上的数据，我们可以达到数据降维的目的。

说到降维，降维就是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的。在实际的生产和应用中，降维在一定的信息损失范围内，可以为我们节省大量的时间和成本。降维也成为应用非常广泛的数据预处理方法，PCA 是降维算法的一种。

1、为什么要有PCA

如果数据之中的某些维度之间存在较强的线性相关关系，那么样本在这两个维度上提供的信息有就会一定的重复，所以我们希望数据各个维度之间是不相关的 (也就是正交的)。此外，出于降低处理数据的计算量或去除噪声等目的，我们也希望能够将数据集中一些不那么重要 (方差小) 的维度剔除掉。

例如在下图中，数据在 x 轴和 y 轴两个维度上存在着明显的相关性，当我们知道数据的 x 值时也能大致确定 y 值的分布。但是如果我们不是探究数据的 x 坐标和 y 坐标之间的关系，那么数据的 x 值和 y 值提供的信息就有较大的重复。在绿色箭头标注的方向上数据的方差较大，而在蓝色箭头方向上数据的方差较小。这时候我们可以考虑利用蓝色和绿色的箭头表示的单位向量来作为新的基底，在新的坐标系中原来不同维度间线性相关的数据变成了线性不相关的。由于在蓝色箭头方向上数据的方差较小，在需要降低数据维度的时候我们可以将这一维度上的数据丢弃并且不会损失较多的信息。如果把丢弃这一维度之后的数据重新变化回原来的坐标系，得到的数据与原来的数据之间的误差不大。这被称为重建误差最小化。PCA 就是进行这种从原坐标系到新的坐标系的变换的。

2、如何计算 PCA

数据经过 PCA 变换之后的各个维度被称为主成分，各个维度之间是线性无关的。为了使变换后的数据各个维度提供的信息量从大到小排列，变换后的数据的各个维度的方差也应该是从大到小排列的。数据经过 PCA 变换之后方差最大的那个维度被称为第一主成分。

我们希望投影后投影值尽可能分散，而这种分散程度，可以用数学上的方差来表述：

$$\mathrm{Var}(a)=\frac{1}{m}\sum _{i=1}^m{\left(a_i-\mu \right)}^2$$

两个降维后的样本的特征轴通过数学上的协方差表示其相关性：

$$\mathrm{Cov}(a,b)=\frac{1}{m}\sum _{i=1}^m\left(a_i-{\mu }_a\right)\left(b_i-{\mu }_b\right)$$

当协方差为0时，表示两个降维后的样本的特征轴线性不相关。

在统计学上，协方差用来刻画两个随机变量之间的相关性，反映的是变量之间的二阶统计特性。考虑两个随机变量 $X_i和X_j$ ，它们的协方差定义为：

$$\mathrm{cov}\left(X_i,X_j\right)=E\left[\left(X_i-E\left(X_i\right)\right)\left(X_j-E\left(X_j\right)\right)\right]$$

$$\mathrm{cov}\left(X_i,X_j\right)=\frac{1}{n-1}\sum _{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)$$

样本均值：

$$\overline{x}=\frac{1}{n}\sum _{i=1}^N{x}_i$$

样本方差：

$$S^2=\frac{1}{n-1}\sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2$$

我们只讨论离散型随机变量的情形下，独立、不相关与协方差为零三者的关系：

• 独立：随机变量 $\xi ,\eta$ 独立是指对于任意的常数a,b，都有$P(\xi =a,\eta =b)=P(\xi =a)\cdot P(\eta =b)$。

• 相关性：相关系数是${\rho }_{\xi \eta }=\frac{\mathrm{cov}(\xi ,\eta )}{\sqrt{\mathrm{var}(\xi )}\sqrt{\mathrm{var}(\eta )}}$，相关系数其实是“线性相关系数”。

相关系数和协方差在描述相关性方面是等价的，但独立与相关性的关系是：独立一定不相关，不相关不一定独立。

协方差矩阵：假设有m个变量，特征维度为2，$a_1$表示变量1的a特征。那么构成的数据集矩阵为：
$$X=\left(\begin{array}{llll}{a}_1& a_2& \dots & a_m\\ b_1& b_2& \dots & b_m\end{array}\right)$$

再假设它们的均值都是0，对于有两个均值为0的m维向量组成的向量组，

$$\frac{1}{m}X{X}^T=\left(\begin{array}{cc}\frac{1}{m}{\sum }_{i=1}^m{a}_i^2& \frac{1}{m}{\sum }_{i=1}^m{a}_i{b}_i\\ \frac{1}{m}{\sum }_{i=1}^m{a}_i{b}_i& \frac{1}{m}{\sum }_{i=1}^m{b}_i^2\end{array}\right)$$

可以发现对角线上的元素是两个降维后的样本的特征轴的方差，其他元素是两个降维后的样本的特征轴的协方差，两者都被统一到了一个矩阵——协方差矩阵中。

PCA 算法的目标：方差max，协方差min。

要达到 PCA 降维目的，等价于将协方差矩阵对角化：即除对角线外的其他元素化为0，并且在对角线上将元素按大小从上到下排列，这样我们就达到了优化目的。

我们先来考虑如何计算第一主成分。假设每一条原始数据是一个 $m$ 维行向量，数据集中有 $n$ 条数据。这样原始数据就可以看作一个 $n$行 $m$ 列的矩阵。我们将其称为 $X$，用$x^{(i)}$代表数据集中的第 $i$ 条数据(也就是 $X$ 的第 $i$ 和行向量)。这里为了方便起见，我们认为原始数据的各个维度的均值都是 0。当原始数据的一些维度的均值不为 0 时我们首先让这一维上的数据分别减去这一维的均值，这样各个维度的均值就都变成了 0。为了使 X 变化到另一个坐标系，我们需要让 $X$ 乘以一个 $m\times m$ 的正交变换矩阵 $W$。$W$视为由列向量$<w_1,w_2,...,w_m>$组成。我们让 $X$ 和 $W$ 进行矩阵相乘之后就可以原始数据变换到新的坐标系中。
$$T=XW$$
为了使变换不改变数据的大小，我们让 $W$ 中的每个列向量 $w_i$ 的长度都为1，也就是$||w_i||=1$。$T$ 中的各个列向量为 $<t_1,t_2,...,t_m>$。为了使第一主成分 $(t_1)$ 的方差最大，
$$\begin{array}{rl}{w}_1& =\arg \underset{\Vert w_1\Vert =1}{\max }\sum _{i=1}^n{\left(t_{1i}\right)}^2\\ & =\arg \underset{\Vert w_1\Vert =1}{\max }\sum _{i=1}^n{\left(x^{(i)}\cdot w_1\right)}^2\\ & =\arg \underset{\Vert w_1\Vert =1}{\max }{w}_1^T{X}^{T}X{w}_1\end{array}$$
上述最优化问题中 $w_1$ 的长度被限制为 1，为了求解 $w_1$ ，我们将其变成如下的形式:
$$w_1=\arg \max \frac{w_1^T{X}^{T}X{w}_1}{w_1^T{w}_1}$$
因为当 $C$ 是一个不为零的常数时，
$$\frac{{\left(C{w}_1\right)}^T{X}^{T}X\left(C{w}_1\right)}{{\left(C{w}_1\right)}^T\left(C{w}_1\right)}=\frac{w_1^T{X}^{T}X{w}_1}{w_1^T{w}_1}$$
这时候求解出的是 $w_1$ 的方向。我们只要在这个方向上长度取长度为 1 的向量就得到了结果。$\frac{w_1^T{X}^{T}X{w}_1}{w_1^T{w}_1}$是一个非常常见的瑞利熵，其更一般的形式是
$$\frac{x^{T}Mx}{x^{T}x}$$
这里的 $M$ 是一个厄米特矩阵 ($HermitianMatrix$)，在本文中我们可以将其认为是一个实对称矩阵；$x$ 是一个长度不为零的列向量。求解瑞利熵的最值需要对实对称矩阵的对角化有一定的了解。这里的$X^{T}X$很显然是一个实对称矩阵。对一个实对称矩阵进行特征值分解，我们可以得到:
$$M=P^{T}DP$$
这里的 $D$ 是一个对角矩阵，对角线上的元素是特征值；$P=<p_1,p_2,...,p_n>$，每个$p_i$都是一个长度为 1 的特征向量，不同的特征向量之间正交。我们将特征值分解的结果带回瑞利熵中可以得到
$$\frac{x^{T}Mx}{x^{T}x}=\frac{x^T{P}^{T}DPx}{x^T{P}^{T}Px}=\frac{{\sum }_i{\lambda }_i{y}_i^2}{{\sum }_i{y}_i^2}=\sum _i{\lambda }_i\frac{y_i^2}{{\sum }_k{y}_k^2}$$
这里的$y_i=p_i\cdot x$。令${\alpha }_i=\frac{y_i^2}{{\sum }_k{y}_k^2}$，这时有$0\ge {\alpha }_i\le 1$且${\sum }_i{\alpha }_i=1$。这样$\frac{x^{T}Mx}{x^{T}x}={\sum }_i{\lambda }_i{\alpha }_i$就构成了一个一维凸包。根据凸包的性质我们可以知道，当最大的${\lambda }_i$对应的${\alpha }_i=1$时整个式子有最大值。所以当 $x$ 的为最大的特征值对应的特征向量时瑞利熵有最大值，这个最大值就是最大的特征值。根据这个结论我们就可以知道$w_1$就是$X^{T}X$的最大的特征值对应的特征向量，第一主成分$t_1=X{w}_1$。这样我们就得到了计算第一主成分的方法。接下来我们继续考虑如何计算其他的主成分。因为 $W$ 是一个正交矩阵，所以
$$w_k=\arg \max \frac{w_k^T{X}^{T}X{w}_k}{w_k^T{w}_k}s.t.w_i^T{w}_k=0,i<k$$
因为 $w_k$ 和 $w_1,w_2,..w_{k-1}$ 正交，
$$\begin{array}{rl}\frac{w_k^T{X}^{T}X{w}_k}{w_k^T{w}_k}& =\frac{{\sum }_{i=1}^m{\lambda }_i{\left(w_k^T{w}_i\right)}^2}{{\sum }_{i=1}^m{\left(w_k^T{w}_i\right)}^2}\\ & =\frac{{\sum }_{i=k}^m{\lambda }_i{\left(w_k^T{w}_i\right)}^2}{{\sum }_{i=k}^m{\left(w_k^T{w}_i\right)}^2}\end{array}$$
为了使第 $k$ 个主成分在与前 $k-1$ 个主成分线性无关的条件下的方差最大，那么 $w_k$ 应该是第 $k$ 大的特征值对应的特征向量。经过这些分析我们就能发现变换矩阵 $W$ 中的每个列向量就是 $X^{T}X$ 的各个特征向量按照特征值的大小从左到右排列得到的。

接下来我们对如何计算 PCA 做一个总结:

1. 把每一条数据当一个行向量，让数据集中的各个行向量堆叠成一个矩阵。
2. 将数据集的每一个维度上的数据减去这个维度的均值，使数据集每个维度的均值都变成 0，得到矩阵 $X$。
3. 计算方阵 $X^{T}X$ 的特征值和特征向量，将特征向量按照特征值由大到小的顺序从左到右组合成一个变化矩阵 $W$。为了降低数据维度，我们可以将特征值较小的特征向量丢弃。
4. 计算 $T=XW$，这里的 $T$ 就是经过 PCA 之后的数据矩阵。

除了这种方法之外，我们还可以使用奇异值分解的方法来对数据进行 PCA 处理，这里不再详细介绍。

3、PCA 的应用

首先我们来看一下 PCA 在数据降维方面的应用。我们在 MNIST 数据集上进行了测试。我们对 MNIST 的测试集中的每一幅 28×28 的图片的变成一个 784 维的行向量，然后把各幅图片拼接成的行向量堆叠一个 784×10000 的数据矩阵。对这个数据矩阵进行 PCA 处理。处理得到的特征值的分布如下图。

MNIST 数据集特征值的分布:

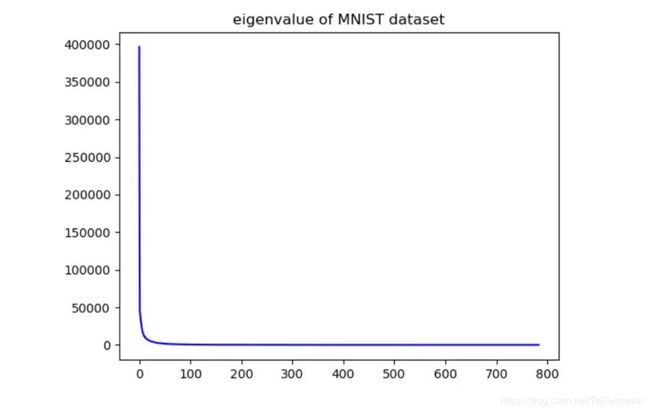
通过图片我们可以看出前面一小部分的特征值比较大，后面的特征值都比较接近于零。接下来我们取前 200，300 个主成分对数据进行重建。我们发现使用前 200 个主成分重建的图像已经能够大致分辨出每个数字，使用前 300 个主成分重建的图像已经比较清晰。根据实验我们可以发现 PCA 能够在丢失较少的信息的情况下对数据进行降维。

原始图像:

使用前 200 个主成分重建的图像:

使用前 300 个主成分重建的图像:

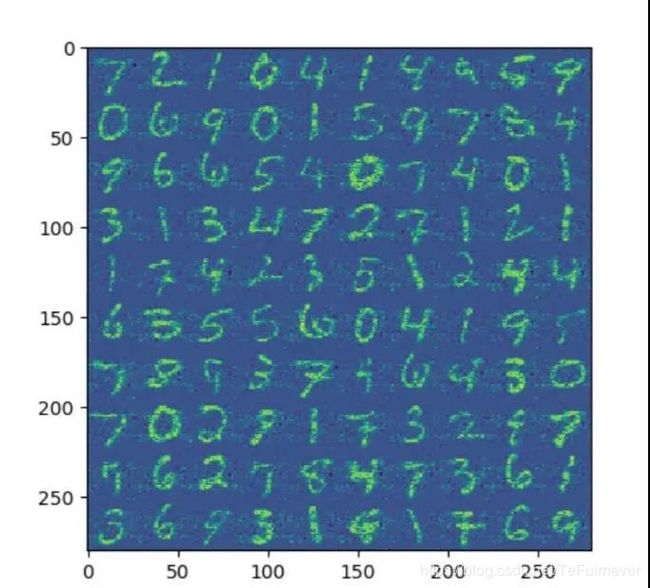
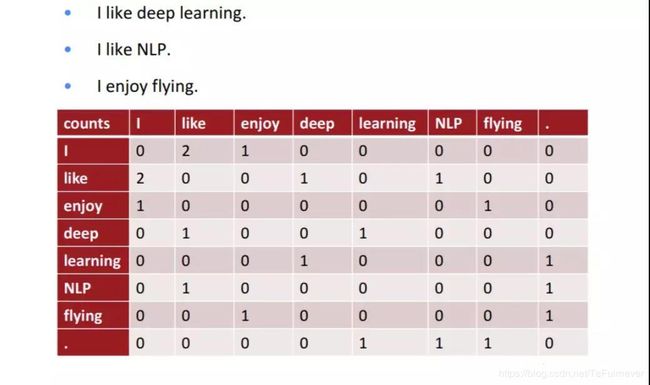
PCA 在自然语言处理方面也有比较多的应用，其中之一就是用来计算词向量。word2vec 是 Google 在 2013 年提出了一个自然语言处理工具包，其思想是用一个向量来表示单词，意思和词性相近的单词对应的向量之间的距离比较小，反之则单词之间的距离比较大。word2vec 原本是使用神经网络计算出来的，本文中的 PCA 也可以被用于计算词向量。

具体的做法为:构建一个单词共生矩阵，然后对这个矩阵进行 PCA 降维，将降维得到的数据作为词向量。使用这种方法构造出的词向量在单独使用时效果虽然不如使用神经网络计算出的词向量，但是将神经网络构造出来的词向量和使用PCA 降维得到的词向量相加之后得到的词向量在表示词语意思时的效果要好于单独使用神经网络计算出来的词向量。

一个共生矩阵的例子:

4、PCA 的缺陷

虽然 PCA 是一种强大的数据分析工具，但是它也存在一定的缺陷。

• 一方面，PCA 只能对数据进行线性变换，这对于一些线性不可分的数据是不利的。为了解决 PCA 只能进行线性变换的问题，Schölkopf, Bernhard 在 1998年提出了 Kernel PCA。Kernel PCA 在计算$M=X^{T}X$的时候不是直接进行相乘，而是使$\overline{m_{ij}}=\Phi {\left(x_i\right)}^T\Phi \left(x_j\right)=K\left(x_i,x_j\right)\}$。这里的$K\left(x_i,x_j\right)$是一个与支持向量机中类似的核函数。这样就能够对数据进行非线性变换。

• 另一方面，PCA 的结果容易受到每一维数据的大小的影响，如果我们对每一维数据乘以一个不同的权重因子之后再进行 PCA 降维，得到的结果可能与直接进行 PCA 降维得到的结果相差比较大。对于这个问题，Leznik 等人在论文Estimating Invariant Principal Components Using Diagonal Regression 中给出了一种解决方案。

• 除此之外，PCA 要求数据每一维的均值都是 0，在将原始数据的每一维的均值都变成 0 时可能会丢失掉一些信息。

虽然 PCA有这些缺陷，但是如果合理的利用，PCA 仍然不失为一种优秀的数据分析和降维的手段。

5、PCA实例

5.1、PCA的Python实现：

# Python实现PCA
import numpy as np

# k is the components you want
def pca(X,k):
	# mean of each feature
    n_samples, n_features = X.shape
    mean=np.array([np.mean(X[:,i]) for i in range(n_features)])
    # normalization
    norm_X=X-mean
    # scatter matrix
    scatter_matrix=np.dot(np.transpose(norm_X),norm_X)
    # Calculate the eigenvectors and eigenvalues
    eig_val, eig_vec = np.linalg.eig(scatter_matrix)
    eig_pairs = [(np.abs(eig_val[i]), eig_vec[:,i]) for i in range(n_features)]
    # sort eig_vec based on eig_val from highest to lowest
    eig_pairs.sort(reverse=True)
    # select the top k eig_vec
    feature=np.array([ele[1] for ele in eig_pairs[:k]])
    # get new data
    data=np.dot(norm_X,np.transpose(feature))
    return data
 
X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
print(pca(X,1))

上面代码实现了对数据$X$进行特征的降维。结果如下：

5.2、用sklearn的PCA与我们的PCA做个比较：

# 用sklearn的PCA
from sklearn.decomposition import PCA
import numpy as np

X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
pca=PCA(n_components=1)pca.fit(X)
print(pca.transform(X))

结果如下：

搞了半天结果不是很一样啊！分析一下吧！

sklearn 中的 PCA 是通过svd_flip函数实现的，sklearn 对奇异值分解结果进行了一个处理。

因为ui*σi*vi=(-ui)*σi*(-vi)，也就是$u$和$v$同时取反得到的结果是一样的，而这会导致通过PCA降维得到不一样的结果（虽然都是正确的）。具体了解可以看参考文章或者自己分析一下 sklearn 中关于 PCA 的源码。

6、PCA的理论推导

PCA 有两种通俗易懂的解释：(1)最大方差理论；(2)最小化降维造成的损失。这两个思路都能推导出同样的结果。

我在这里只介绍最大方差理论：

在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。样本在$u1$上的投影方差较大，在$u2$上的投影方差较小，那么可认为$u2$上的投影是由噪声引起的。

因此我们认为，最好的k维特征是将n维样本点转换为k维后，每一维上的样本方差都很大。

比如我们将下图中的4个点投影到某一维上，这里用一条过原点的直线表示（数据已经中心化）：


假设我们选择两条不同的直线做投影，那么左右两条中哪个好呢？根据我们之前的方差最大化理论，左边的好，因为投影后的样本点之间方差最大（也可以说是投影的绝对值之和最大）。

计算投影的方法见下图：

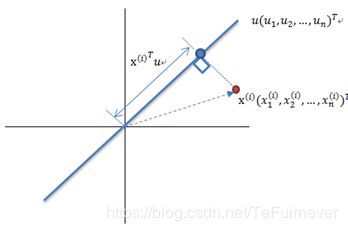
图中，红色点表示样例，蓝色点表示在$u$上的投影，$u$是直线的斜率也是直线的方向向量，而且是单位向量。蓝色点是在$u$上的投影点，离原点的距离是$<x,u>$（即$X^{T}U$或者$U^{T}X$）。

7、选择降维后的维度K(主成分的个数)

如何选择主成分个数$K$呢？先来定义两个概念：

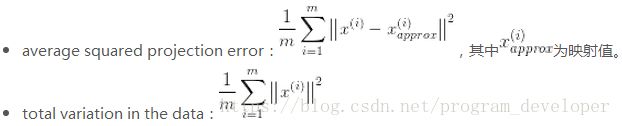
选择不同的$K$值，然后用下面的式子不断计算，选取能够满足下列式子条件的最小$K$值即可。

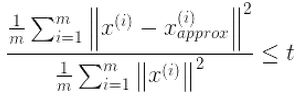
其中t值可以由自己定，比如t值取0.01，则代表了该 PCA 算法保留了99%的主要信息。当你觉得误差需要更小，你可以把t值设置的更小。上式还可以用 SVD 分解时产生的S矩阵来表示，如下面的式子：

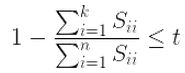
参考文章：

• 主成分分析（PCA）原理详解
• 理解主成分分析 (PCA)
• 主成分分析PCA（Principal Component Analysis）在sklearn中的应用及部分源码分析