机器学习算法原理总结系列---算法基础之(13)模糊C均值聚类(Fuzzy C-means Clustering)
笔者在韩国Chonnam National University攻读硕士学位,FCM算法是professer Lim在这学期主要授课的内容,他说他刚发一篇FCM结合遗传算法还有各种脑电信号处理,搭建分析AD病人的EEG信号的计算智能模型。反正就是各种难。
一、原理详解
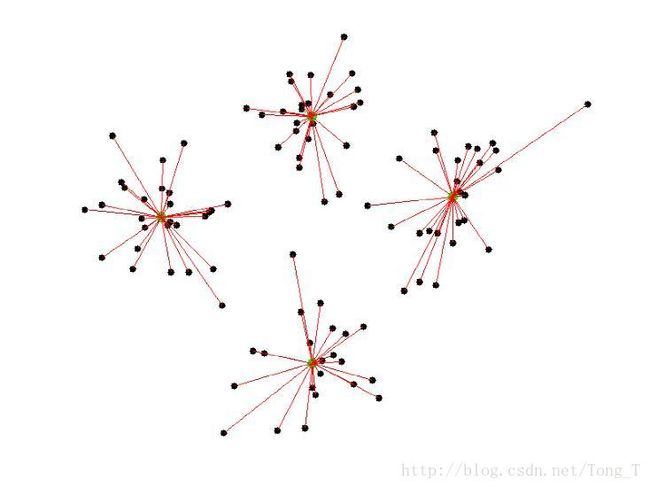
模糊c-均值聚类算法 fuzzy c-means algorithm (FCMA)或称( FCM)。在众多模糊聚类算法中,模糊C-均值( FCM) 算法应用最广泛且较成功,它通过优化目标函数得到每个样本点对所有类中心的隶属度,从而决定样本点的类属以达到自动对样本数据进行分类的目的。
什么是聚类?

假设样本集合为X={x1 ,x2 ,…,xn },将其分成c 个模糊组,并求每组的聚类中心cj ( j=1,2,…,C) ,使目标函数达到最小。
C-Means Clustering:
固定数量的集群。
每个群集一个质心。
每个数据点属于最接近质心对应的簇。

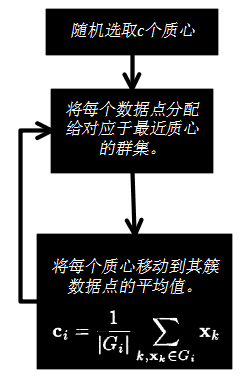
集群是模糊集合。
一个点的隶属度可以是0到1之间的任何数字。
一个点的所有度数之和必须加起来为1。
具体的教程大家参考这个教程:
http://home.deib.polimi.it/matteucc/Clustering/tutorial_html/cmeans.html
K均值和模糊C均值的区别:
k均值聚类:一种硬聚类算法,隶属度只有两个取值0或1,提出的基本根据是“类内误差平方和最小化”准则;
模糊的c均值聚类算法:一种模糊聚类算法,是k均值聚类算法的推广形式,隶属度取值为[0 1]区间内的任何一个数,提出的基本根据是“类内加权误差平方和最小化”准则;
这两个方法都是迭代求取最终的聚类划分,即聚类中心与隶属度值。两者都不能保证找到问题的最优解,都有可能收敛到局部极值,模糊c均值甚至可能是鞍点。
K均值和C均值,其实有种C是包含在K中的感觉,C只是特定的实现方式,K均值是广义的概念。
二、代码实现
期中作业就是使用iris数据集搭建无监督学习Fuzzy c-means模型,完成算法,测试算法的成功分类率。
数据集:

FuzzyCmeans_model.py
from numpy import dot, array, sum, zeros, outer, any
# Fuzzy C-Means class
class FuzzyCMeans(object):
"""
Fuzzy C-Means convergence.
Use this class to instantiate a fuzzy c-means object. The object must be
given a training set and initial conditions. The training set is a list or
an array of N-dimensional vectors; the initial conditions are a list of the
initial membership values for every vector in the training set -- thus, the
length of both lists must be the same. The number of columns in the initial
conditions must be the same number of classes. That is, if you are, for
example, classifying in ``C`` classes, then the initial conditions must have
``C`` columns.
There are restrictions in the initial conditions: first, no column can be
all zeros or all ones -- if that happened, then the class described by this
column is unnecessary; second, the sum of the memberships of every example
must be one -- that is, the sum of the membership in every column in each
line must be one. This means that the initial condition is a perfect
partition of ``C`` subsets.
"""
def __init__(self, training_set, initial_conditions, m=2.):
"""
Initializes the algorithm.
:Parameters:
training_set
A list or array of vectors containing the data to be classified.
Each of the vectors in this list *must* have the same dimension, or
the algorithm won't behave correctly. Notice that each vector can be
given as a tuple -- internally, everything is converted to arrays.
initial_conditions
A list or array of vectors containing the initial membership values
associated to each example in the training set. Each column of this
array contains the membership assigned to the corresponding class
for that vector. Notice that each vector can be given as a tuple --
internally, everything is converted to arrays.
m
This is the aggregation value. The bigger it is, the smoother will
be the classification. Please, consult the bibliography about the
subject. ``m`` must be bigger than 1. Its default value is 2
"""
self.__x = array(training_set)
self.__mu = array(initial_conditions)
self.m = m
'''The fuzzyness coefficient. Must be bigger than 1, the closest it is
to 1, the smoother the membership curves will be.'''
self.__c = self.centers()
def __getc(self):
return self.__c
def __setc(self, c):
self.__c = array(c).reshape(self.__c.shape)
c = property(__getc, __setc)
'''A ``numpy`` array containing the centers of the classes in the algorithm.
Each line represents a center, and the number of lines is the number of
classes. This property is read and write, but care must be taken when
setting new centers: if the dimensions are not exactly the same as given in
the instantiation of the class (*ie*, *C* centers of dimension *N*, an
exception will be raised.'''
def __getmu(self):
return self.__mu
mu = property(__getmu, None)
'''The membership values for every vector in the training set. This property
is modified at each step of the execution of the algorithm. This property is
not writable.'''
def __getx(self):
return self.__x
x = property(__getx, None)
'''The vectors in which the algorithm bases its convergence. This property
is not writable.'''
def centers(self):
"""
Given the present state of the algorithm, recalculates the centers, that
is, the position of the vectors representing each of the classes. Notice
that this method modifies the state of the algorithm if any change was
made to any parameter. This method receives no arguments and will seldom
be used externally. It can be useful if you want to step over the
algorithm. *This method has a colateral effect!* If you use it, the
``c`` property (see above) will be modified.
:Returns:
A vector containing, in each line, the position of the centers of the
algorithm.
"""
mm = self.__mu ** self.m
c = dot(self.__x.T, mm) / sum(mm, axis=0)
self.__c = c.T
return self.__c
def membership(self):
"""
Given the present state of the algorithm, recalculates the membership of
each example on each class. That is, it modifies the initial conditions
to represent an evolved state of the algorithm. Notice that this method
modifies the state of the algorithm if any change was made to any
parameter.
:Returns:
A vector containing, in each line, the membership of the corresponding
example in each class.
"""
x = self.__x
c = self.__c
M, _ = x.shape
C, _ = c.shape
r = zeros((M, C))
m1 = 1. / (self.m - 1.)
for k in range(M):
den = sum((x[k] - c) ** 2., axis=1)
if any(den == 0):
return self.__mu
frac = outer(den, 1. / den) ** m1
r[k, :] = 1. / sum(frac, axis=1)
self.__mu = r
return self.__mu
def step(self):
"""
This method runs one step of the algorithm. It might be useful to track
the changes in the parameters.
:Returns:
The norm of the change in the membership values of the examples. It
can be used to track convergence and as an estimate of the error.
"""
old = self.__mu
self.membership()
self.centers()
return sum(self.__mu - old) ** 2.
def __call__(self, emax=1.e-10, imax=20):
"""
The ``__call__`` interface is used to run the algorithm until
convergence is found.
:Parameters:
emax
Specifies the maximum error admitted in the execution of the
algorithm. It defaults to 1.e-10. The error is tracked according to
the norm returned by the ``step()`` method.
imax
Specifies the maximum number of iterations admitted in the execution
of the algorithm. It defaults to 20.
:Returns:
An array containing, at each line, the vectors representing the
centers of the clustered regions.
"""
error = 1.
i = 0
while error > emax and i < imax:
error = self.step()
i = i + 1
return self.cmain.py
# -*- coding:utf-8 -*-
import random
from fuzzy_model import FuzzyCMeans
# used for randomising U
global MAX
MAX = 10000.0
def load_data(file):
data = []
cluster_location = []
with open(str(file), 'r') as f:
for line in f:
current = line.split(",")
current_dummy = []
for j in range(0, len(current) - 1):
current_dummy.append(float(current[j]))
j += 1
# print current[j]
if current[j] == "Iris-setosa\n":
cluster_location.append(0)
elif current[j] == "Iris-versicolor\n":
cluster_location.append(1)
else:
cluster_location.append(2)
data.append(current_dummy)
return data, cluster_location
def randomise_data(data):
"""
This function randomises the data,
and also keeps record of the order of randomisation.
"""
order = list(range(0, len(data)))
random.shuffle(order)
new_data = [[] for _ in range(0, len(data))]
for index in range(0, len(order)):
new_data[index] = data[order[index]]
return new_data, order
def initialise_U(data, cluster_number):
"""
This function would randomis U such that the rows add up to 1.
it requires a global MAX.
"""
global MAX
U = []
for i in range(0, len(data)):
current = []
rand_sum = 0.0
for j in range(0, cluster_number):
dummy = random.randint(1, int(MAX))
current.append(dummy)
rand_sum += dummy
for j in range(0, cluster_number):
current[j] = current[j] / rand_sum
U.append(current)
return U
def normalise_U(U):
"""
This de-fuzzifies the U, at the end of the clustering.
It would assume that the point is a member of the cluster
whose membership is maximum.
"""
for i in range(0, len(U)):
maximum = max(U[i])
for j in range(0, len(U[0])):
if U[i][j] != maximum:
U[i][j] = 0
else:
U[i][j] = 1
return U
def de_randomise_data(data, order):
"""
This function would return the original order of the data,
pass the order list returned in randomise_data() as an argument
"""
new_data = [[] for i in range(0, len(data))]
for index in range(len(order)):
new_data[order[index]] = data[index]
return new_data
def checker_iris(final_location):
"""
This is used to find the percentage correct match with
the real clustering.
"""
right = 0.0
for k in range(0, 3):
checker = [0, 0, 0]
for i in range(0, 50):
for j in range(0, len(final_location[0])):
if final_location[i + (50 * k)][j] == 1:
checker[j] += 1
right += max(checker)
answer = right / 150 * 100
return str(answer) + " % accuracy"
if __name__ == '__main__':
data, cluster_location = load_data("iris.txt")
# print(data)
data, order = randomise_data(data)
# print("========")
# print(cluster_location)
initU = initialise_U(data, 3)
# print('init membership matrix')
# print(initU)
# This parameter measures the smoothness of convergence
m = 2.0
fcm = FuzzyCMeans(data, initU, m)
print ('Optimal clustering center')
print (fcm(emax=0))
print ('Optimal membership matrix')
print (fcm.mu)
nu = normalise_U(fcm.mu)
final_location = de_randomise_data(nu, order)
print(checker_iris(final_location))实验结果为:
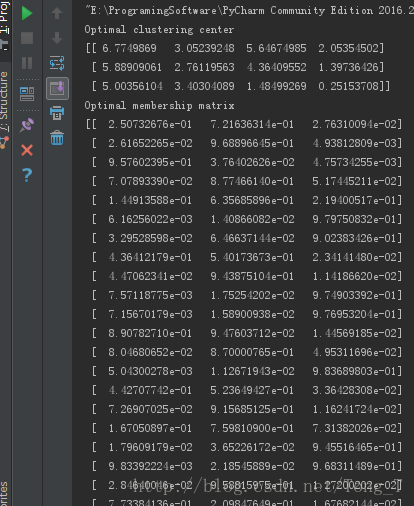

在无监督学习中,FuzzyCmeans的分类表现还是很不错的。
网上还有以为大牛写的基于IRIS数据集的代码,大家可以去看看:
http://blog.csdn.net/zwqhehe/article/details/75174918
昨天我还在一个视频中听到说,监督学习深度网络现在特别火,大家都想在这方面做出点成绩,而非监督学习这边,由于分类效果并不是特别好,所以大家很少关注到它,也很少去研究这个方向。但是你想想,我们人生下来,从无到有,从小到大,我们很多东西都没有训练学习标签,都是一种无监督的学习,所以这方面还是有很大的研究价值。