二叉树及特殊的二叉树
一、二叉树的定义
二叉树(Binary Tree)是n(n≥0)个节点的有限集合,n = 0时,该集合为空集合称为空二叉树,或者由一个根节点和两棵互不相交的,分别称为根节点的左子树和右子树的二叉树组成。
二、二叉树的特点
- 每个节点最多有两颗子树(也就是说每个节点最多有两个子节点),所以在二叉树中不存在度大于2的节点。
- 左子树和右子树是有顺序的,次序不能颠倒。
- 即使树中某节点只有一棵子树,也要区分是左子树还是右子树。
三、特殊二叉树
1、斜树
所有的节点都只有左子树的二叉树叫左斜树;所有节点都只有右子树的二叉树叫由斜树。这两者统称为斜树。斜树的特点很明显就是每一层只有一个节点,节点的个数与二叉树的深度相同。其实线性表可以理解为树的一种极其特殊的形式。
2、满二叉树
在一棵二叉树中,如果所有分支节点都存在左子树和右子树,并且所有的叶子节点都在同一层上,这样的二叉树称为”满二叉树“。如下图:
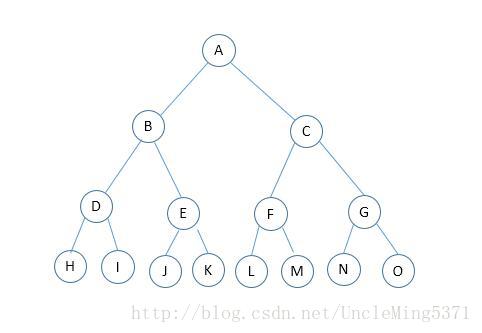
满二叉树的特点:
(1) 叶子只能出现在最下一层。
(2)非叶子节点的度一定为2。
(3)在同样深度的二叉树中,满二叉树的节点个数最多,叶子数最多。
3、完全二叉树
对于一棵具有n个节点的二叉树按照层序编号,如果编号为i(1≤ i ≤ n)的节点与同样深度的满二叉树中编号为i的节点在二叉树中位置完全相同,则这棵二叉树称为”完全二叉树“。如下图:
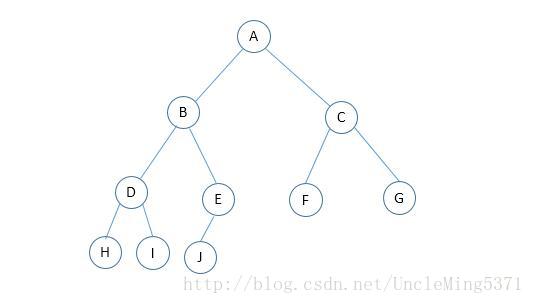
把完全二叉树的节点与同样深度的满二叉树各个节点进行编号比较,所有节点出现的位置相同,则是完全二叉树。所以, 满二叉树一定是一棵完全二叉树,而完全二叉树不一定是满二叉树。
完全二叉树的特点:
(1) 叶子节点只能出现在最下两层。
(2)最下层的叶子一定集中左部连续位置。
(3)倒数第二层,若有叶子节点,一定都在右部连续位置。
(4)如果节点度为1,则该节点只有左孩子,即不存在右子树的情况。
(5)同样节点的二叉树,完全二叉树的深度最小。
三、二叉树的性质
1、在二叉树的第i层上至多有2^(i-1)个节点(i≥1);比如第3层,至多有4个节点;
2、深度为k的二叉树至多有2^k - 1个节点(k≥1);
3、对任何一颗二叉树T,如果某终端节点数为n0, 度为2的节点数为n2,则n0 = n2 + 1;
4、具有n个节点的完全二叉树的深度log2(n) + 1 个(|X|表示不大于X的最大整数)。
5、如果对一棵有n个节点的完全二叉树的节点按层序编号,对任一节点i(1≤ i ≤ n)有:
(1)如果i = 1, 则节点i是二叉树的根;如果i > 1,则父节点是 i / 2 ;
(2)如果2i > n,则节点i是叶子节点,否则其左子节点是2i;
四、二叉树存储结构
1、二叉树顺序存储结构
二叉树的顺序存储结构就是用一维数组存储二叉树中的节点,并且节点的存储位置,也就是数组下标要能够体现出节点之间的逻辑关系,比如父子关系、左右节点关系等。
对于如下图一棵完全二叉树:
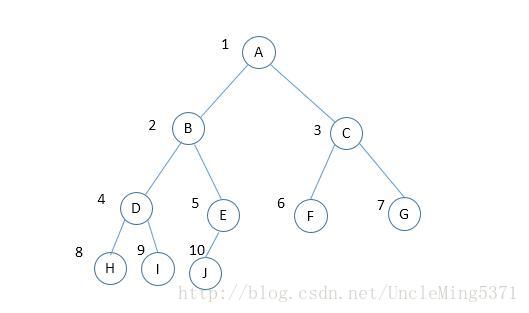
顺序存储结构如下:

通过上面的存储结构,可以通过数组的下标体现出节点之间的逻辑关系,比如节点A的下标i是0,则
2 * i + 1 是节点A的左节点,即节点B是A的左节点;2 *( i + 1) 是节点A的右节点,即节点C是A的右节点。对于一棵完全二叉树,可以很好的利用上面的存储结构,数组的每个位置都有值,但是对于普通二叉树,由于节点不是连续的形式,对于一些极端的情况可能只存在右子树,不存在左子树,则数组中会存在大量的存储空间被浪费,此时可以考虑另一种存储结构——二叉链表。
2、二叉链表
由于二叉树的每个节点最多有两个孩子,所以二叉链表的每个节点有一个数据域和两个指针域,指针域分别指向左子节点和右子节点。存储结构如下:

二叉链表表示法数据结构比较简单,这里不在做过多的描述。
五、二叉树遍历
二叉树的遍历是指从根节点出发,按照某种次序依次访问二叉树中的所有节点,使得每个节点被访问一次且仅被访问一次。以下面所示的二叉树为例,分析各种遍历方式的结果。如下图:

1、前序遍历
先访问根节点,然后前序遍历左子树,再前序遍历右子树。
遍历步骤:
(1)先访问根节点A,结果为A;
(2)前序遍历根节点A的左子树,左子树的根节点是B,此时结果是AB;
(3)继续前序遍历以B为根节点的左子树,此时的根节点是D,结果为:ABD;
(4)继续遍历以D为根节点的左子树H,此时结果为:ABDH;
(5)节点H不存在左子树,则遍历以D为根节点的右子树,此时结果为:ABDHI;
(6)递归遍历以B为根节点右子树E,由于E存在左子树J,此时结果为:ABDHIE;
(7)E存在左子树,此时结果为:ABDHIEJ;此时根节点A的左子树遍历完成,开始遍历右子树;
(8)右子树根节点为C,此时结果为:ABDHIEJC;
(9)以C为根节点的子树存在左节点F,结果变为:ABDHIEJCF;
(10)节点F不存在子节点,遍历C的右节点,前序遍历最后结果为:ABDHIEJCFG;
2、中序遍历
先中序遍历根节点的左子树,然后访问根节点,再中序遍历右子树。
遍历步骤:
(1)根节点A存在左子树,先中序遍历以节点B为根节点的左子树;
(2)节点B存在左子树,中序遍历以节点D为根节点的左子树;
(3)节点D存在左叶子节点H,此时结果为:HD;
(4)节点D存在右叶子节点I,此时结果为:HDI;
(5)以节点B为根节点的左子树遍历完成,此时访问根节点B,结果为:HDIB;
(6)访问B节点的有子树,右子树根节点存在左节点J,此时结果为:HDIBJE;
(7)根节点A的左子树访问完成,访问根节点A,结果变为:HDIBJEA;
(8)遍历根节点A的右子树,右子树存在左叶子节点F,此时结果为:HDIBJEAF;
(9)然后访问右子树的根节点C,中序遍历最后结果为:HDIBJEAFCG;
3、后序遍历
先后序遍历根节点的左子树,然后后序遍历根节点的右子树,再访问根节点。
遍历步骤:
(1)根节点A存在左子树,先后续遍历以节点B为根节点的左子树;
(2)节点B存在左子树,后续遍历以节点D为根节点的左子树;
(3)节点D存在左叶子节点H,右子节点I,此时结果为:HID;
(4)节点B存在右子树,后续遍历以节点D为根节点的右子树;
(5)节点E存在左叶子节点,不存在右子节点,此时结果为:HIDJE;
(6)B节点的左子树、右子树遍历完成,访问B节点,结果为:HIDJEB;
(7)根节点的左子树遍历完成,后序遍历根节点的右子树,结果为:HIDJEBFGC;
(8)最后访问根节点,后序遍历最后结果为:HIDJEBFGCA;
4、层级遍历
从根所在的层开始,从上而下逐层进行遍历,在同一层中,按左到右的顺序对节点逐个访问。
遍历步骤:
(1)从第一层根节点开始访问,结果为:A;
(2)访问第二层,从左到右,结果为:ABC;
(3)访问第三层,结果为:ABCDEFG;
(4)访问第四层,层级遍历结果为:ABCDEFGHIJ;