根号类算法讲解——各(四)种莫队(填坑)

这个坑终于填了…
上文接这里

莫队算法

这就是莫队(确信)

先放个可离线的题：

可离线：给你个序列，m次询问(可离线)一段区间有多少个不同的数(可离线)(数据范围 105 10 5 )可离线

相信各位都已经拿高效的DS秒掉了

相信大家看完题目第一感觉就是离线(
考虑两次询问区间 (l,r) ( l , r ) 和 (l′,r′) ( l ′ , r ′ ) ，假设我们已经处理出 (l,r) ( l , r ) 区间内的答案，考虑将其拓展到 (l′,r′) ( l ′ , r ′ )

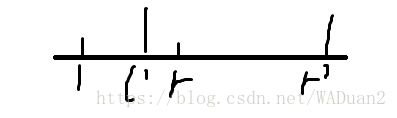
也就是要将左端点从 l l 移动到 l′ l ′ ，右端点从 r r 移动到 r′ r ′ ，一个数一个数的移动，复杂度就是 O(|l′−l|+|r′−r|) O ( | l ′ − l | + | r ′ − r | )

对于每个询问用这种方法拓展到下一个询问，就可以求出所有的答案啦！
(这**不就是暴力吗(╯`□′)╯┴—┴

上面的做法随便想想都是 O(n2) O ( n 2 ) 的…
那该怎么办(傻*博主举报了

莫队的小核心：

对询问离线，将区间分为 n−−√ n 块，将询问以
1.左端点在同一块中的，按右端点排序；
2.左端点不在同一块中的，按左端点所在块排序；

之后再进行刚才说的暴力，复杂度就变成 n1.5 n 1.5 的啦！

复杂度证明：

1.左端点在同一块中的询问：
一个块中最多有 n n 个询问，每次左端点最多移动 n−−√ n 次，右端点一共移动最多 n n 次(因为右端点已经从小到大排好序)，所以总复杂度 O(n1.5) O ( n 1.5 ) (就是左端点移动的总复杂度)
2.左端点不再同一块中的询问：
最多跨 n−−√ n 块，每次跨越左端点最多移动 n−−√ n 次，右端点最多移动 n n 次，所以总复杂度 n1.5 n 1.5
包含1,2两种情况的证明类似，复杂度一样 n1.5 n 1.5

(说了这么多，我选择nlogn的DS

莫队使用条件：

0.能用莫队过
1.能将询问离线
2.可以往外拓展或收缩

说了这么多，回到刚才的小例题，直接看代码吧

#include
#include
#include
#include
#define N 200050
using namespace std;
inline int read(){
    int x=0,f=1;char c;
    do c=getchar(),f=c=='-'?-1:f; while(!isdigit(c));
    do x=(x<<3)+(x<<1)+c-'0',c=getchar(); while(isdigit(c));
    return x*f;
}
int n,m,Block_size;
int block[N],a[N],ans[N],l=1,r;///l=1,r=0代表初始状态(空区间)
int cnt[1000050],tmp;
struct Query{
    int l,r,id;
}q[N];///问题
inline bool cmp(Query a,Query b){
    return block[a.l]==block[b.l]?a.r///排序，同一块内按右端点排，否则按块排
}
inline void Update(int x,int k){///cnt[i]代表i颜色在区间出现的次数，k=-1代表删除，k=1代表插入
    if(!cnt[x]) tmp++;///如果开始没这个数字，这次操作会使这个数字出现，那么数字数(tmp)+1
    cnt[x]+=k;
    if(!cnt[x]) tmp--;///如果操作导致这个数字变没了，就要-1
}
int main(){
    n=read();///区间长度
    Block_size=sqrt(n);///分块
    for(int i=1;i<=n;i++){
        a[i]=read();///读入区间
        block[i]=(i-1)/Block_size+1;///每个位置属于哪块
    }
    m=read();
    for(int i=1;i<=m;i++){
        q[i].l=read();q[i].r=read();
        q[i].id=i;///读入询问
    }
    sort(q+1,q+m+1,cmp);///对询问排序
    for(int i=1;i<=m;i++){
        while(l1);
        ///如果左端点想去的(q[i].l)在实际(l)的右面，删去最左面的点(少一个点)
        while(l>q[i].l) Update(a[--l],1);
        ///如果左端点想去的(q[i].l)在实际(l)的左面，往左拓展一个点(多一个点)
        while(r1);///同理
        while(r>q[i].r) Update(a[r--],-1);
        ans[q[i].id]=tmp;///存答案
    }
    for(int i=1;i<=m;i++){
        printf("%d\n",ans[i]);///输出结果
    }
return 0;
}

带修改莫队

可如果有些问题带修改，怎么办？

带修莫队在原先的二维拓展(l,r)上增加了一个时间维(t)，在移动的时候也要移动t使得时间也满足限制

排序方式：左端点所在的块为第一关键字，右端点所在的块为第二关键字，上一个修改操作的时间为第三关键字

剩下的内容就和普通莫队一样了

复杂度玄学 O(n53) O ( n 5 3 )

题我这个月一定补上！

树莫队

树上莫队其实就是将树化为区间后进行普通莫队

首先弄出一棵树的括号序(入栈时候记一次，出栈时候记一次)

就比如这棵树

括号序是ABCCBDEEFFDA

对每个点记录两次出现的位置(设为 s s 和 t t )

对于每组询问 (x,y) ( x , y ) (设 x x 比 y y 深度小)：
1.如果两个点在一条链上( x x 是 y y 祖先)，答案为 (x.t,y.t) ( x . t , y . t )
2.否则，答案为(x.s,y.t)+lca(x,y)

区间内出现两次的节点信息抵消

YY一下发现并没有什么问题，所以是对的(

回滚莫队

有些题维护的信息加一个元素简单删一个难….

就需要回滚莫队

这个我还没写过(我这个月一定写)，我看了别人的讲解自己口胡一下

就是设左端点在这个块内的询问，右端点的集合为 S S ，你可以通过处理下一个块最左面的点到 S S 的答案，再由它向左延伸得到这个块内的答案

没写过，这几天写写，有错误就回来改