莫队算法讲解（含树上莫队）

莫队算法

莫队算法是一种离线算法，通常不能有修改 操作。
其通过对询问操作的执行顺序进行更改，然后使用最暴力的方法，可以达到很好的复杂度。

首先，如果要用莫队算法，则必须满足已知ans[ l , r ]可以得到ans[ l +1, r ],ans[ l -1, r ],ans[ l , r +1],ans[ l , r -1]。

莫队算法的实现步骤为：
1、先对原序列进行分块。
2、离线操作，对询问进行排序，以左端点所在块编号 为第一关键字，右端点的位置为第二关键字，进行排序。然后维护[ l , r ]的答案，并不断调整 l 和 r 。

我们来分析一下时间复杂度：
1、左端点所在块编号确定时，右端点位置单调不下降，所以右端点移动最多造成的时间复杂度是 O ( n )的，总共 n√ 块，总时间复杂度为 O ( nn√ )。

2、左端点所在块编号进行变动时，右端点移动最多造成的时间复杂度是 O ( n )，总共 n√ 块，变动次数也就是 n√ 次，总时间复杂度为 O ( nn√ )。

3、块内左端点位置每次最多移动 n√ ，一共 m 次询问，也就是一共移动 m 次，总时间复杂度为 O ( mn√ )。

总的来说，时间复杂度是 32 次的，这是十分优秀的。

树上莫队

树上莫队是莫队算法的拓展，思想依然差不多，下面我介绍一种树上莫队的做法。

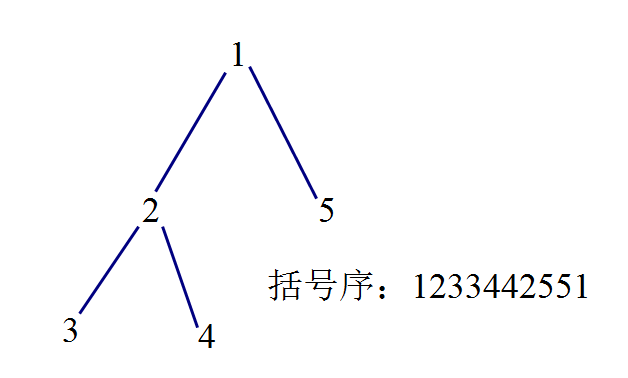
首先弄出树的括号序。（对树做一次深搜，第一次进入某节点时，将此节点编号加入序列，从某节点退出时，将此节点编号第二次加入序列）
如图，有一棵树，以及它的括号序：

然后记录一个数在括号序中第一次出现和最后一次出现的位置。
如果要询问 j 到 k 之间路径的信息，需进行分类讨论：
（以下均遵循此原则，出现两次的数字不算入所求信息中）
1、如果 j 是 k 的祖先，那么所求信息就为 j 和 k 最后出现的位置之间的信息。
2、如果 j 不是 k 的祖先。那么所求信息就为 j 最先出现的位置以及 k 最后出现的位置之间的信息，我们发现， j , k 的 lca 不在其中，再把 lca 加上即可。

那么实现的时候就是用 cha 来表示一个点的出现情况的改变。
然后当做序列上的莫队来做就可以了。

拓展：带修改的莫队

其实莫队还是可以带修改的。O(∩_∩)O~~
带修改的莫队其实也不难，我们三元组（l,r,x）来排序，x表示在此次询问操作之前经过了x次修改操作。同样的，知道( l , r , x )的答案可以知道( l -1, r , x )( l +1, r , x )( l , r -1, x )( l , r +1, x )( l , r , x -1)( l , r , x +1)的答案，一样可以用莫队算法。

块大小需要设置为 n23 ，总时间复杂度是 O ( n53 )，证明略。