深度剖析主席树（静态）

主席树（chairman tree）（据说是被chairman传开的）

它是一种专门用来实现求区间第K大这类操作的数据结构

 

Q：这不是分块轻松解决的事吗？

A：是的，但是分块时间为的，而主席树是的

Q：这是不是很难，代码复杂度极高？

A：NoNoNo，代码复杂度一点都不高，前置知识只有动态开点线段树

Q：那我不会怎么办？

A：右转自行度娘，或者菜鸡的博客  

 

菜鸡很菜，刚学了主席树，还是最简单的静态

首先思考一下，区间求第K大，最暴力的解自然是每次排序，是

Q：如果用数据结构维护呢？

 A：每次询问用一棵权值线段树或者权值树状数组+二分维护，也是,QAQ，（不会可见可怜的狗狗这道题）

 

权值树状数组+二分姑且不论，我们只谈权值线段树（时间复杂度低才是王道）

每次询问的是一段区间，与区间相关的算法没有多少，也就前缀和，线段树……

权值线段树下标记的是值的大小，存的是出现次数，所以具有可加减性

故选用前缀和

——————————————————————————————————————

前面的引导就差不多结束了，进入正文了

 

主席树=前缀和+线段树=对每个前缀和中的点开一棵权值线段树（下标记的是权值的线段树）

线段树上的结点记录个数中，大小在区间中的数的个数

 

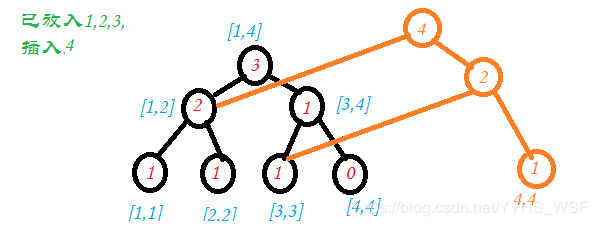
建立棵线段树，不动态开点必定超空间，动态开点后，将新的树建立在原来的树之上

每次只用新插入一个结点，

如果该结点应该在左子树，右子树就不用变；反之左子树不用变

每次新插入只用，总共建个结点就够了

	void add(int &p,int l,int r,int x)
	{
		lc[++cnt]=lc[p],rc[cnt]=rc[p],s[cnt]=s[p]+1,p=cnt;
		if(l==r) return;
		int mid=l+r>>1;
		if(x<=mid) add(lc[p],l,mid,x);
			else add(rc[p],mid+1,r,x);
	}  //lc为左儿子，rc为右儿子，s为结点个数

 

查询：由于上文提到线段树具有可减性，只用在的线段树的线段树找第K大，这算是权值线段树的基本操作吧

（不会可见可怜的狗狗这道题，也可以看代码）

	int kth(int p1,int p2,int l,int r,int x)
	{
		if(l==r) return l;
		int xx=s[lc[p2]]-s[lc[p1]];
		int mid=l+r>>1;
		if(x<=xx) return kth(lc[p1],lc[p2],l,mid,x);
			else return kth(rc[p1],rc[p2],mid+1,r,x-xx); 
	}

 

总结：主席树就是前缀和+线段树的思想毒瘤了一点（有心人可以看出我上面的引导是倒推的），但是只要你熟练掌握线段树，知道思想后小菜一碟

例题（时刻更新）

1、Luogu P3834 【模板】可持久化线段树 1（主席树）

   额，模板题，加个离散化就号了

   

#include
#include
using namespace std;

const int N=4e6+5;
int n,m,rt[N],b[N];
struct A{int id,x; }a[N];

bool cmp(A x,A y)
{
	return x.x>1;
		if(x<=mid) add(lc[p],l,mid,x);
			else add(rc[p],mid+1,r,x);
	}
	
	int kth(int p1,int p2,int l,int r,int x)
	{
		if(l==r) return l;
		int xx=s[lc[p2]]-s[lc[p1]];
		int mid=l+r>>1;
		if(x<=xx) return kth(lc[p1],lc[p2],l,mid,x);
			else return kth(rc[p1],rc[p2],mid+1,r,x-xx); 
	}
}zxs;
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) 
		a[i].id=i,scanf("%d",&a[i].x);
	sort(a+1,a+n+1,cmp);
	int tot=0;
	for(int i=1;i<=n;i++) b[a[i].id]=i;
	for(int i=1;i<=n;i++)
		rt[i]=rt[i-1],zxs.add(rt[i],1,n,b[i]);
	while(m--)
	{
		int l,r,k; scanf("%d%d%d",&l,&r,&k);
		printf("%d\n",a[zxs.kth(rt[l-1],rt[r],1,n,k)].x);
	}
	return 0;
}

2、可怜的狗狗（这是超链接）

模板题*2

3、Luogu P3919 【模板】可持久化数组（可持久化线段树/平衡树）

模板题*3

4、BZOJ 2223: [Coci 2009]PATULJCI 

模板题，查询中位数相同的是否超过序列长度的一半