吴恩达机器学习第三周------(2)神经网络向前传播算法识别手写数字(Python实现)
声明:本人为机器学习初学者,此博文纯为个人学习总结之用,难免出现纰漏错误之处,欢迎各位批评指正,不惜吝教!
编程环境:Anaconda3 , Python3.7
编程练习介绍
在本练习中,您将使用与之前编程作业(逻辑回归识别手写数字)中相同的训练集,从而实现神经网络向前传播算法的手写数字识别。 神经网络相比较逻辑回归而言,能够表示非线性假设的复杂模型。而逻辑回归不能形成更复杂的假设,因为它只是一个线性分类器.。本次的编程练习,还将使用已经训练过的神经网络中的参数。 您的目标是实现向前传播算法并使用我们的参数进行预测。 在下周的练习中,将编写神经网络参数的反向传播算法。
数据分析
本次的编程练习,提供两个文件分别是:ex3data1.mat 和 ex3weights.mat 点击链接即可获取
- ex3data1.mat 中包含5000个手写数字训练示例的数据集: 0~9 中十个数字,每个数字有500个样式。共5000样本数据。
每个训练样例 20像素*20像素 ,展开成向量为400维行向量,由于每个训练样例都为数据矩阵X中的一行,所以X 5000行 400列 , 而标签矩阵y 5000行 1列。ex3data1.mat中的数据部分信息如下图所示:
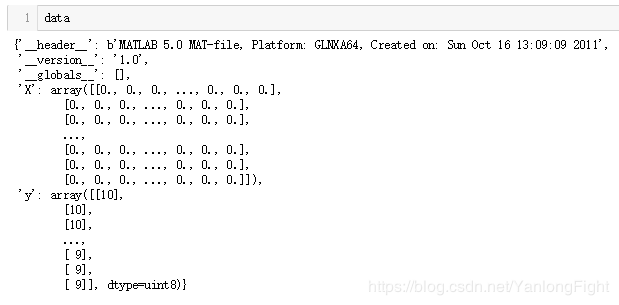
- ex3weights.mat 中是已经帮我们训练好的参数theta1和theta2,ex3weights.mat中的数据部分信息如下图所示:

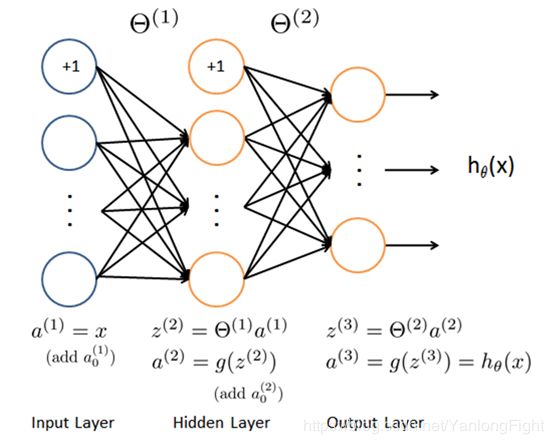
模型表示
使用神经网络的第一件事,就是建立神经网络模型,即确定神经网络的层数以及每层神经单元的数量。神经网络模型由三层构成:输入层,隐藏层,输出层。通常输入层的神经单元数即我们训练集的特征数量,而输出层的神经单元数即我们训练集结果的类的数量。我们真正要确定的是隐藏层的层数和每个中间层的单元数,而一个合理的默认选项:只使用单个隐藏层。如果隐藏层数大于1,应尽量确保每个隐藏层的神经单元个数相同,通常情况下隐藏层神经单元的个数越多越好,即使大量的神经单元会导致计算量大的问题。一般来说,每个隐藏层所包含的神经单元数量还应当和输入X的纬度即特征的数量相匹配或呈现倍数关系。
由于我们的输入是数字图像的像素值,并且像素的图像尺寸为20像素*20像素,因此我们应设置400个输入层神经单元(不包括额外的偏置神经元),设置10个输出层神经单元,对应10个数字类,至于隐藏层,规定设置隐藏层的层数为一层,隐藏层的神经单元数量为25个。
- 输入层:400个神经单元
- 隐藏层:25个神经单元
- 输出层:10个神经单元
实现过程
import numpy as np
import scipy.io as sio
# 导入 ex3data1.mat 文件数据
data = sio.loadmat('ex3data1.mat')
raw_X = data['X']
raw_y = data['y']
为 raw_X 前插入一列值为1的数 ,赋值给 X
X = np.insert(raw_X,0,values=1,axis=1)
X.shape
# (5000, 401)
y = raw_y.flatten()
y.shape
# (5000,)
# 导入 ex3weights.mat 文件数据
theta = sio.loadmat('ex3weights.mat')
theta.keys()
# dict_keys(['__header__', '__version__', '__globals__', 'Theta1', 'Theta2'])
获取到已经训练好的参数theta1和theta2
theta1 = theta['Theta1']
theta2 = theta['Theta2']
theta1.shape,theta2.shape
# ((25, 401), (10, 26))
定义sigmoid函数
def sigmoid(z):
return 1/ (1 + np.exp(-z))
向前传播
a1 = X
z2 = X @theta1.T
a2 = sigmoid(z2)
a2.shape
# (5000, 25)
a2 = np.insert(a2,0,values=1,axis=1)
a2.shape
# (5000, 26)
z3 = a2 @ theta2.T
a3 = sigmoid(z3)
a3.shape
# (5000, 10)
y_pred = np.argmax(a3,axis=1)
y_pred = y_pred + 1
acc = np.mean(y_pred == y)
acc
# 0.9752
a3
# array([[1.12661530e-04, 1.74127856e-03, 2.52696959e-03, ...,
4.01468105e-04, 6.48072305e-03, 9.95734012e-01],
[4.79026796e-04, 2.41495958e-03, 3.44755685e-03, ...,
2.39107046e-03, 1.97025086e-03, 9.95696931e-01],
[8.85702310e-05, 3.24266731e-03, 2.55419797e-02, ...,
6.22892325e-02, 5.49803551e-03, 9.28008397e-01],
...,
[5.17641791e-02, 3.81715020e-03, 2.96297510e-02, ...,
2.15667361e-03, 6.49826950e-01, 2.42384687e-05],
[8.30631310e-04, 6.22003774e-04, 3.14518512e-04, ...,
1.19366192e-02, 9.71410499e-01, 2.06173648e-04],
[4.81465717e-05, 4.58821829e-04, 2.15146201e-05, ...,
5.73434571e-03, 6.96288990e-01, 8.18576980e-02]])