特征分解，奇异值分解（SVD） 和隐语义模型（LFM）

[摘要]
特征分解——>奇异值分解（SVD）——>隐语义模型（LFM），三个算法在前者的基础上推导而成，按顺序先后出现。三者均用于矩阵降维。其中：

• 特征分解可用于主成分分析。（可参考博主文章主成分分析）
• 奇异值分解（SVD）和隐语义模型（LFM）可用于推荐系统中，将评分矩阵补全、降维。

为什么进行矩阵分解：

• 有人说，将大型矩阵分解为简单矩阵乘积的形式，为了减少计算量。矩阵分解及应用毕业论文_豆丁网
• 有人说，在自然语言处理和推荐系统中，会有非常稀疏的矩阵，把稀疏矩阵分解成高阶特征的线性组合，便于分类和预测。通俗地理解矩阵分解的意义

接下来按推导顺序讲解

1 特征分解

1.1 为什么进行特征分解？（目的）

将矩阵降维。

1.2 什么样的矩阵可以进行特征分解？（前提）

1. 待降维的矩阵是方阵。
2. $(A-\lambda E)x=0$有非零解，即 $|A-\lambda E|=0$。

1.3 特征分解的原理

1. 特征分解使用到矩阵的特征值，所以先了解特征值的概念。
   $$Ax=\lambda x$$
   上式中，$\lambda$是矩阵$A$的一个特征值，$x$是矩阵$A$的特征值$\lambda$对应的特征向量，是一个$n$维向量。
   站在特征向量的角度，特征向量的几何含义是：特征向量$x$通过方阵$A$变换，只缩放，方向不变。（即$x$左乘一个方阵的效果，等同于$x$乘以一个数值。$Ax$称为矩阵变换，$\lambda x$称为矩阵缩放，变换的效果与缩放相同。）
   站在方阵$A$的角度：$n\times n$的方阵$A$通过右乘一个矩阵$x$，可以变换成一个$n\times 1$的列向量。

2. 得到方阵$A$的$n$个特征值，组成对角矩阵$\sum$：
   $$\sum =\left\{\begin{array}{ccccc}{\lambda }_1& 0& 0& ...& 0\\ 0& {\lambda }_2& 0& ...& 0\\ 0& 0& ...& ...& 0\\ ...& ...& ...& {\lambda }_{n-1}& 0\\ 0& ...& 0& 0& {\lambda }_n\end{array}\right\}$$

3. 则方阵$A$的特征分解就可以表示为：
   $$A=U\sum U^{-1}$$
   其中$U$是$n$个特征向量组成的$n\times n$维方阵，$\sum$是这$n$个特征值为主对角线的$n\times n$维方阵。

4. 可以将 方阵$A$的特征分解进一步表示：
   将$n$ 个特征向量标准化（可使用施密特正交化方法）：
   
   
   便可以满足$U^{-1}=U^T$，这时方阵A的特征分解可以进一步写成：
   $$A=U\sum U^T$$

1.4 特征分解的手推计算

1.5 特征分解的Python实现

NumPy

import numpy as np
A = np.array([[1,2,3],
             [4,5,6],
             [7,8,9]])
# 计算特征值
print(np.linalg.eigvals(A))
# 同时计算特征值和特征向量
eigvals,eigvectors = np.linalg.eig(A)
print(eigvals)
print(eigvectors)

Scipy

import numpy as np
import scipy as sp
A = np.array([[1,2,3],
             [4,5,6],
             [7,8,9]])
# 计算特征值
print(sp.linalg.eigvals(A))
# 同时计算特征值和特征向量
eigvals,eigvectors = sp.linalg.eig(A)
print(eigvals)
print(eigvectors)

参考网址：【深度学习基础】：线性代数(一)_特征分解及numpy、scipy实现

2 奇异值分解（SVD）

2.1 为什么进行奇异值分解？（目的）

矩阵是方阵，可以分解，方法是1中的特征分解（$A=U\cdot \sum \cdot U^T$）。
矩阵不是方阵，即列数和行数不等，也可以分解，最常用的分解方法是奇异值分解（SVD）。

2.2 什么样的矩阵可以进行奇异值分解？（前提）

任意矩阵。

2.3 奇异值分解的原理

2.3.1 奇异值分解公式

有$n\times n$的矩阵A，将其进行奇异值分解，公式如下：
$$A=U\sum V^T$$
其中，

• U（叫做左奇异值，$U$的列叫做左奇异向量）是$m\times m$的方阵，
• $V$（对应的，$V$叫右奇异值，V的列叫做右奇异向量）是$n\times n$的方阵，
• $\sum$是$m\times n$的矩阵，主对角线元素称为奇异值，其他元素均为0。

进一步的，

• U的列是$A{A}^T$的特征向量，
• $V$（注意，公式中使用时，需要进行转置。即$V^T$的行是$A^{T}A$的特征向量）的列是$A^{T}A$的特征向量。
• $A{A}^T$与$A^{T}A$的特征值相同，为$\left\{{\lambda }_1、{\lambda }_2、...{\lambda }_r\right\}$， $\sum$主对角线上的奇异值${\sigma }_i=\sqrt{{\lambda }_i}$。一般奇异值会有多个，而我们只使用top-k个构成这个对角阵。

2.3.2 奇异值分解的手推计算

参考文献：
PCA为什么使用协方差矩阵
奇异值的物理意义是什么？
两篇文章都非常不错，建议阅读。

2.3.3 奇异值分解的Python实现

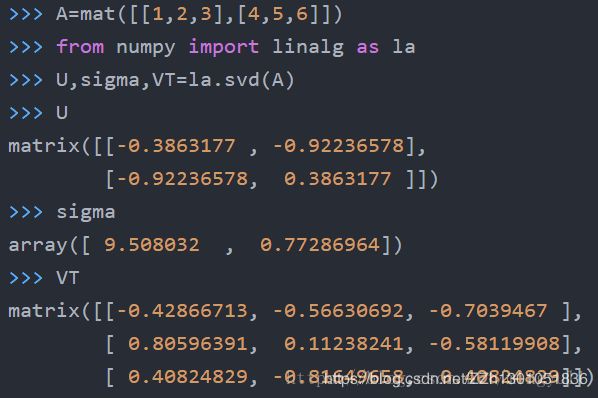
(1) numpy.linalg.svd() 程序实现

有一点需要注意，sigma本来应该跟A矩阵的大小2*3一样，但linalg.svd()只返回了一个行向量的sigma，并且只有2个奇异值（本来应该有3个），这是因为第三个奇异值为0，舍弃掉了。之所以这样做，是因为当A是非常大的矩阵时，只返回奇异值可以节省很大的存储空间。当然，如果我们要重构A，就必须先将sigma转化为矩阵。

（2）svd用于降维

# 奇异值分解(SVD)
import numpy as np

#原始矩阵n*m
A = np.mat([[1,2,3],
            [4,5,6],
            [7,8,9]])
U, sigma, VT = np.linalg.svd(A)
print('===原始===')
print('A = ',A)
print('U = ', U)
print('sigma = ', sigma)
print('VT = ', VT)

print("===用k个描述，描述前后值A与newA相差不多===")
k = 1 #特征值共两个，我们用最大的top-1个奇异值和对应的U和V中的向量来描述矩阵A。
newU = U[:,:k]
newSig = np.mat(np.eye(k)*sigma[:k])
newVT = VT[:k,:]
newA = newU*newSig*newVT
print('newU = ',newU)
print('newSig = ', newSig)
print('newVT = ', newVT)
print('newA = ', newA)

print("降维:由n*m维降低到n*k维")
xformedA = A.T*newU*newSig.T
print(xformedA)

输出

===原始===
A =  [[1 2 3]
 [4 5 6]
 [7 8 9]]
U =  [[-0.21483724  0.88723069  0.40824829]
 [-0.52058739  0.24964395 -0.81649658]
 [-0.82633754 -0.38794278  0.40824829]]
sigma =  [1.68481034e+01 1.06836951e+00 4.41842475e-16]
VT =  [[-0.47967118 -0.57236779 -0.66506441]
 [-0.77669099 -0.07568647  0.62531805]
 [-0.40824829  0.81649658 -0.40824829]]
===用k个描述，描述前后值A与newA相差不多===
newU =  [[-0.21483724]
 [-0.52058739]
 [-0.82633754]]
newSig =  [[16.84810335]]
newVT =  [[-0.47967118 -0.57236779 -0.66506441]]
newA =  [[1.73621779 2.07174246 2.40726714]
 [4.2071528  5.02018649 5.83322018]
 [6.6780878  7.96863051 9.25917322]]
降维
[[-136.15878258]
 [-162.471513  ]
 [-188.78424343]]

2. numpy.linalg.svd方法
   函数：np.linalg.svd(a,full_matrices=1,compute_uv=1)。

参数：

• a是一个形如(M,N)矩阵
• full_matrices的取值是为0或者1，默认值为1，这时u的大小为(M,M)，v的大小为(N,N) 。否则u的大小为(M,K)，v的大小为(K,N) ，K=min(M,N)。
• compute_uv的取值是为0或者1，默认值为1，表示计算u,s,v。为0的时候只计算s。

返回值：
总共有三个返回值u,s,v
u大小为(M,M)，s大小为(M,N)，v大小为(N,N)。
A = usv
其中s是对矩阵a的奇异值分解。s除了对角元素不为0，其他元素都为0，并且对角元素从大到小排列。s中有n个奇异值，一般排在后面的比较接近0，所以仅保留比较大的r个奇异值。

参考网址：Python之SVD介绍

3 隐语义模型（LFM）