SVD 奇异值分解

Vectors 向量

向量通常用头上有一个箭头的小写字母表示，如$x$。构成向量的数字叫做分向量（components），分向量的数量等于向量的维度（dimensionality of the vector）。
$$x=\left(\begin{array}{c}8\\ 6\\ 7\\ 5\\ 3\end{array}\right)$$
上面的例子表示了一个5维的向量，$x_1=8,x_2=6$，向量也可以水平表示来节省空间，例如$x=[8,6,7,5,3]$。普遍来说，一个$n$维向量$x$是一个$n$个数字的序列，分向量$x_i$表示在第$i$维的$x$的值。

Matrices 矩阵

矩阵和表格很像。矩阵由行（row，横向的列表）和列（column，纵向的列表）组成。
$$A=\left[\begin{array}{cccccc}17& 18& 5& 5& 45& 1\\ 42& 28& 30& 15& 115& 3\\ 10& 10& 10& 21& 51& 2\\ 28& 5& 65& 39& 132& 5\\ 24& 26& 45& 21& 116& 4\end{array}\right]$$
矩阵的大小（或者说维度）是由矩阵的行数和列数决定的，上面的矩阵就是一个$5\times 6$大小的矩阵。通常来说，矩阵用大写字母表示，例如$A$，矩阵的行数用$m$表示，列数用$n$表示。矩阵的元素（entries or elements or components）表示为小写的$a$，这个元素$a$的位置是由它所在的行数$i$和列数$j$表示。举例来说，132在矩阵的第4行第5列，$a_{45}=132$。在第$i$行第$j$列的元素表示为$a_{ij}$，叫做$ij-entry$或$ij-compnent$。

Matrix Notation 矩阵表示

$m,n$是两个大于1的整数，令$a_{ij},i=1,...,m,j=1,...,n$，由数字组成的矩阵
$$A=\left[\begin{array}{ccccc}{a}_{11}& ...& a_{1j}& ...& a_{1n}\\ .& & .& & .\\ a_{i1}& ...& a_{ij}& ...& a_{in}\\ .& & .& & .\\ a_{m1}& ...& a_{mj}& ...& a_{mn}\end{array}\right]$$
是一个$m\times n$大小的矩阵，$a_{i}j$是A的元素。数字序列
$$A_{(i)}=(a_{i1},...,a_{(in)})$$
是矩阵的第$i$行，数字序列
$$A^{(j)}=(a_{1j},...,a_{(mj)})$$
是矩阵的第$j$行。
矩阵可以看作是一些向量的集合，一个$n$维的向量可以看作是一个$1\times n$的矩阵。

Vector Terminology 向量术语

Vector Length 向量长度

向量$v$的长度表示为$|v|$。它的计算公式为
$$|v|=\sqrt{\sum _{i=1}^n{x}_i^2}$$
例如，$v=[4,11,8,10]$,那么它的长度
$$|v|=\sqrt{4^2+11^2+8^2+10^2}=\sqrt{301}$$

Vector Addition 向量加法

将两个向量相加，就是把$v_1$里面的元素与$v_2$里相对应的元素相加，如果
$A=[a_1,a_2,...,a_n],B=[b_1,b_2,...,b_n]$, 那么$A+B=[a_1+b_1,a_2+b_2,...,a_n+b_n]$。

Scalar Multiplication 标量乘法

将一个标量（实数）和一个向量相乘，就是把向量里面的每个元素与这个标量相乘。如果$d$是一个实数，$v$代表一个向量$v_1,v_2,...,v_n$，那么$d\ast v=[d{v}_1,d{v}_2,...,d{v}_n]$。

Inner Product 内积

两个向量的内积代表将两个向量的每个对应的元素相乘然后将这些结果相加，表示为$(v_1,v_2)$或者$v_1\cdot v_2$，$(v_1,v_2)=v_1\cdot v_2={\sum }_{i=1}^n{x}_i{y}_i$

Orthogonality 正交

如果两个向量的内积为0，那么这两个向量是正交的。

Normal Vector or Unit Vector 单位向量

向量长度为1的向量可以叫做单位向量。任何向量长度大于0的向量可以通过将每个元素除以向量长度的方法正规化（normalized）为单位向量。
例如：
令$v=[2,4,1,2]$，那么它的长度为
$$|v|=\sqrt{2^2+4^2+1^2+2^2}=5$$
那么$u=[2/5,4/5,1/5,1/5]$是一个单位向量，因为
$$|u|=\sqrt{(2/5{)}^2+(4/5{)}^2+(1/5{)}^2+(1/5{)}^2}=1$$

Orthonormal Vectors

两个正交的单位向量叫做orthonormal。

Gram-Schmidt Orthonormalization Process

将一组向量变成互相正交的单位向量
例如
$$A=\left[\begin{array}{ccc}1& 2& 1\\ 0& 2& 0\\ 2& 3& 1\\ 1& 1& 0\end{array}\right]$$
转换为一组正交的单位向量
$$A=\left[\begin{array}{ccc}\frac{\sqrt{6}}{6}& \frac{\sqrt{2}}{6}& \frac{2}{3}\\ 0& \frac{2\sqrt{2}}{3}& -\frac{1}{3}\\ \frac{\sqrt{6}}{3}& 0& 0\\ \frac{\sqrt{6}}{6}& -\frac{\sqrt{2}}{6}& -\frac{2}{3}\end{array}\right]$$
首先，单位化$v_1=[1,0,2,1]$
$$u_1=[\frac{1}{\sqrt{6}},0,\frac{2}{\sqrt{6}},\frac{1}{\sqrt{6}}]$$
然后，令
$$\begin{array}{rl}{w}_2=v_2-u_1\cdot v_2\ast u_1=& [2,2,3,1]-[\frac{1}{\sqrt{6}},0,\frac{2}{\sqrt{6}},\frac{1}{\sqrt{6}}]\cdot [2,2,3,1]\ast [\frac{1}{\sqrt{6}},0,\frac{2}{\sqrt{6}},\frac{1}{\sqrt{6}}]\\ =& [2,2,3,1]-\frac{9}{\sqrt{6}}\ast [\frac{1}{\sqrt{6}},0,\frac{2}{\sqrt{6}},\frac{1}{\sqrt{6}}]\\ =& [2,2,3,1]-[\frac{3}{2},0,3,\frac{3}{2}]\\ =& [\frac{1}{2},2,0,-\frac{1}{2}]\end{array}$$
把$w_2$正规化，得到
$$v_2=[\frac{\sqrt{2}}{6},\frac{2\sqrt{2}}{3},0,-\frac{\sqrt{2}}{6}]$$
同理可得，
$$u_3=[\frac{2}{3},-\frac{1}{3},0,-\frac{2}{3}]$$
一般来说，有一组向量，那么
$$w_k=v_k-\sum _{i=1}^{k-1}{u}_t\cdot v_k\ast u_t$$

Matrix Terminology 矩阵术语

Square Matrix 方块矩阵

如果一个矩阵的行数和列数相同，那么这个矩阵是方块矩阵。

Transpose 转置

一个矩阵的转置矩阵是通过将原本的矩阵的每个元素交换行和列来生成的。$A$的转置矩阵表示为$A^T$。例如
$$A=\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\end{array}\right]$$
那么$A$的转置矩阵为
$$A^T=\left[\begin{array}{cc}1& 4\\ 2& 5\\ 3& 6\end{array}\right]$$

Matrix Multiplication 矩阵乘法

$m\times n$大小的矩阵$A$可以和$n\times s$大小的矩阵$B$相乘得到$m\times s$大小的矩阵$AB$。
矩阵$AB$的每一个位置的值$a{b}_{ij}=A_i\cdot B^j$

Identity Matrix 单位矩阵

一个对角线为1其他都是0的方块矩阵叫做单位矩阵$I$。
$$AI=A$$

Orthogonal Matrix 正交矩阵

如果$A{A}^T=A^{T}A=I$，那么$A$就是正交矩阵。

Diagonal Matrix 对角矩阵

如果一个矩阵除了对角线其他都是0，只有对角线有非0值，那么这个矩阵是对角矩阵。

Determinant 行列式

$A$的行列式表示为$|A|$或$\det (A)$。
$$\begin{array}{rl}|A|=\left|\begin{array}{ccc}a& b& c\\ d& e& f\\ g& h& i\end{array}\right|=& a\left|\begin{array}{ccc}.& .& .\\ .& e& f\\ .& h& i\end{array}\right|-b\left|\begin{array}{ccc}.& .& .\\ d& .& f\\ g& .& i\end{array}\right|+c\left|\begin{array}{ccc}.& .& .\\ d& e& .\\ g& h& .\end{array}\right|\\ =& a\left|\begin{array}{cc}e& f\\ h& i\end{array}\right|-b\left|\begin{array}{cc}d& f\\ g& i\end{array}\right|+c\left|\begin{array}{cc}d& e\\ g& h\end{array}\right|\\ =& aei+bfg+cdh-ceg-bdi-afh\end{array}$$

Eigenvectors and Eigenvalues 特征向量和特征值

一个能满足下列条件的非零向量叫做特征向量
$$Av=\lambda v$$
其中，$A$是一个方块矩阵，$\lambda$是一个纯量，$v$就是特征向量，$\lambda$叫做特征值。
例如，有一个矩阵
$$A=\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]$$
那么
$$Av=\lambda v=\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\lambda \left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$$
所以
$$\begin{gathered} 2x_1+x_2=\lambda x_1 \\ {x}_1+2x_2=\lambda x_2 \end{gathered}$$
可以转变为
$$\begin{gathered} (2-\lambda )x_1+x_2=0 \\ {x}_1+(2-\lambda )x_2=0 \end{gathered}$$
让向量$[x_1,x_2]$非0的充分且必要条件是系数矩阵要为0，那么就有
$$\begin{gathered} \left|\begin{array}{cc}(2-\lambda )& 1\\ 1& (2-\lambda )\end{array}\right|=0 \\ (2-\lambda )(2-\lambda )-1\cdot 1=0 \\ {\lambda }^2-4\lambda +3=0 \\ (\lambda -3)(\lambda -1)=0 \\ {\lambda }_1=3,{\lambda }_2=1 \end{gathered}$$
对于$\lambda =3$,可得$x_1=x_2$，所以一种可能的特征向量为$[1,1]$。
对于$\lambda =1$,可得$x_1=-x_2$，所以一种可能的特征向量为$[1,-1]$。

Singular Value Decomposition（SVD）

可以从三个观点来看SVD。

1. 可以将其看作是将一组互相关联的变量转换为一组互不相关的变量的方法，这个方法可以揭示原本数据项之间的关系。
2. SVD可以找出变化最剧烈的数据维度，这样就可以用更少的维度来表示原始数据
3. SVD可以看作是一种压缩数据的方法。

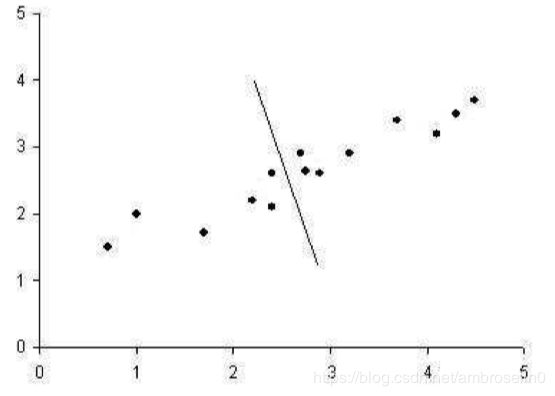
举个例子，下图有一堆点来表示2维的数据，这根线是这些点的最佳线性回归，用一根线（一维）来表示这些点（二维）。

这里的线是一维的个人理解是其中一项值可以用另一项表示，所以只要有一个变数就能确定数据，所以这个线是一维的。

某种意义上，这根线是这笔资料的最佳近似，因为这一条线使各个点到这条线的距离总和最小。如果我们在每个点画一个与这条线垂直的线，并且交点作为原始数据的近似值，那么就可以利用这条回归线作为原始数据的表示，压缩原始数据，并且尽可能的接近于原始数据。

如果有这么一条与上图的线垂直的线，如下图。这条线沿着数据的第二维尽可能的捕捉了尽量多的变化，但是它在近似数据方面表现不佳，因为它表现出了较少变化的维度。

SVD的基本思想：将高维度、高度变化的数据集压缩到低维度的空间，从而更加清晰表现原数据，并且将原市数据从高度变化到低变化排序。在NLP中大量使用SVD的原因是可以在简单的忽略某些值的情况下大量的减少数据，同时保持原来数据的主要关系。

Example of Full Singular Value Decomposition

SVD基于一个线性代数的定理，该定理表明一个矩阵$A$可以分解为三个矩阵的乘积：

1. 正交矩阵$U$
2. 对角矩阵$S$
3. 正交矩阵$U$的转置矩阵$V$

表示为
$$A_{mn}=U_{mm}{S}_{mn}{V}_{nn}^T$$
这里的$U^{T}U=I,V^{T}V=I$，$U$的列是$A{A}^T$的正交特征向量，$V$的特征是$A^{T}A$的正交特征向量，$S$是一个对角矩阵，包含有$U$或者$V$的特征值的平方根，以降序排列。
下面这个例子仅将其应用于小矩阵来计算它的SVD。
首先，有一个矩阵
$$A=\left[\begin{array}{ccc}3& 1& 1\\ -1& 3& 1\end{array}\right]$$
为了计算$U$，得先计算$A{A}^T$，$A^T$为
$$A^T=\left[\begin{array}{cc}3& -1\\ 1& 3\\ 1& 1\end{array}\right]$$
所以
$$A{A}^T=\left[\begin{array}{ccc}3& 1& 1\\ -1& 3& 1\end{array}\right]\left[\begin{array}{cc}3& -1\\ 1& 3\\ 1& 1\end{array}\right]=\left[\begin{array}{cc}11& 1\\ 1& 11\end{array}\right]$$
接下来，要计算$A{A}^T$的特征向量和特征值，特征向量的定义为$Av=\lambda v$，带入这个公式可得
$$\left[\begin{array}{cc}11& 1\\ 1& 11\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\lambda \left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$$
重写为方程组
$$\begin{gathered} 11x_1+x_2=\lambda x_1 \\ {x}_1+11x_2=\lambda x_2 \end{gathered}$$
重组，可得
$$\begin{gathered} (11-\lambda )x_1+x_2=0 \\ {x}_1+(11-\lambda )x_2=0 \end{gathered}$$
系数矩阵的行列式为0来求解$\lambda$
$$\left|\begin{array}{cc}(11-\lambda )& 1\\ 1& (11-\lambda )\end{array}\right|=0$$
求解可得${\lambda }_1=10,{\lambda }_2=12$。对于${\lambda }_1=10$来说，带入可得$x_1=-x_2$，选取$[1,-1]$作为特征向量；对于${\lambda }_2=12$来说，带入可得$x_1=x_2$，选取$[1,1]$作为特征向量。这两个特征向量作为列向量组成的矩阵，按相应特征值的大小排序。换句话说，特征向量大的那一个作为列1，小的那一个作为列2。
$$\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]$$
最后，要将这个转换为一组正交的单位向量。首先正规化$v_1$
$$u_1=\frac{v_1}{|v_1|}=\frac{[1,1]}{\sqrt{1^2+1^2}}=[\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]$$
$$\begin{array}{rl}{w}_2=& v_2-u_1\cdot v_2\ast u_1\\ =& [1,-1]-[\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]\cdot [1,-1]\ast [\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]\\ =& [1,-1]-0\ast [\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]\\ =& [1,-1]\end{array}$$
正规化可得
$$u_2=\frac{w_2}{|w_2|}=[\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}]$$
所以
$$U=\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\end{array}\right]$$
同理，可得
$$V=\left[\begin{array}{ccc}\frac{1}{\sqrt{6}}& \frac{2}{\sqrt{5}}& \frac{1}{\sqrt{30}}\\ \frac{2}{\sqrt{6}}& -\frac{1}{\sqrt{5}}& \frac{2}{\sqrt{30}}\\ \frac{1}{\sqrt{6}}& 0& -\frac{5}{\sqrt{30}}\end{array}\right]$$
同时，特征值为${\lambda }_1=0,{\lambda }_2=10,{\lambda }_3=12$。
需要的是$V$的转置矩阵
$$V^T=\left[\begin{array}{ccc}\frac{1}{\sqrt{6}}& \frac{2}{\sqrt{6}}& \frac{1}{\sqrt{6}}\\ \frac{2}{\sqrt{5}}& -\frac{1}{\sqrt{5}}& 0\\ \frac{1}{\sqrt{30}}& \frac{2}{\sqrt{30}}& -\frac{5}{\sqrt{30}}\end{array}\right]$$
对于$S$来说，按大小顺序将特征值排序塞入到对角线上（这里使用$U$或者$V$的特征值都可以，因为总是一样）。因为这里做的是Full SVD，所以要在$S$后面赛上0列向让它的大小为$m\times n$。$U$中的列成为左特征向量，$V$中的列称为右特征向量。
$$S=\left[\begin{array}{ccc}\sqrt{12}& 0& 0\\ 0& \sqrt{10}& 0\end{array}\right]$$
$$\begin{array}{rl}{A}_{mn}=U_{mm}{S}_{mn}{V}_{nn}^T=& \left[\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\end{array}\right]\left[\begin{array}{ccc}\sqrt{12}& 0& 0\\ 0& \sqrt{10}& 0\end{array}\right]\left[\begin{array}{ccc}\frac{1}{\sqrt{6}}& \frac{2}{\sqrt{6}}& \frac{1}{\sqrt{6}}\\ \frac{2}{\sqrt{5}}& -\frac{1}{\sqrt{5}}& 0\\ \frac{1}{\sqrt{30}}& \frac{2}{\sqrt{30}}& -\frac{5}{\sqrt{30}}\end{array}\right]=\left[\begin{array}{ccc}3& 1& 1\\ -1& 3& 1\end{array}\right]\end{array}$$

Example of Reduced Singular Value Decomposition

要把一个数据压缩到$K$维，做法与上面相同，但是只取$V$的前$K$列。作为数据的压缩结果。

Reference

https://davetang.org/file/Singular_Value_Decomposition_Tutorial.pdf