机器学习之路(四)之感知机算法PLA
基本介绍:
如果训练集数据是两个互不相交的凸集的子集,那么可以找到一个支撑超平面将两个子集分开。那么,如果这个超平面是一个n维的线性方程,就称之为线性分类器。线性分类器是最简单和最基本的分类器,也是最早的神经网络模型,称为感知机模型。
感知机是线性分类器的一种,属于判别模型。包含一个算法框架和激活函数。算法框架就是我们熟悉的线性方程组的一个变换:
![]()
主要是记录一下学习了一种简单的感知机模型,PLA全称是Perceptron Linear Algorithm,即线性感知机算法,属于一种最简单的感知机(Perceptron)模型。
这里分享一下大佬红色石头老师的笔记链接:https://blog.csdn.net/red_stone1/article/details/70866527,理论十分的详细。
然后分享一下实现的例子
数据集介绍:
data1.csv —— 维度为100x3,包含100个样本,前两列是数据特征,最后一列是输出标签label。该数据集线性可分。
data2.csv —— 维度为100x3,包含100个样本,前两列是数据特征,最后一列是输出标签label。该数据集线性不可分。
数据集以及代码可以再github上查看https://github.com/feijuan/ML
# PLA算法-学习自红色石头老师
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv('./data/data1.csv', header=None)
# 样本输入,维度(100,2)
X = data.iloc[:,:2].values
# 样本输出,维度(100,)
y = data.iloc[:,2].values
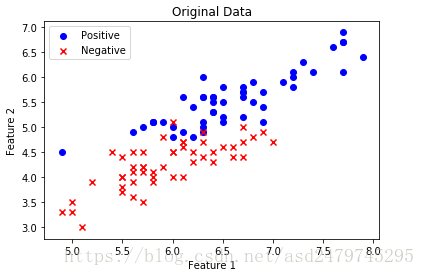
plt.scatter(X[:50, 0], X[:50, 1], color='blue', marker='o', label='Positive')
plt.scatter(X[50:, 0], X[50:, 1], color='red', marker='x', label='Negative')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend(loc = 'upper left')
plt.title('Original Data')
plt.show()
# 均值
u = np.mean(X, axis=0)
# 方差
v = np.std(X, axis=0)
X = (X - u) / v
# 作图
plt.scatter(X[:50, 0], X[:50, 1], color='blue', marker='o', label='Positive')
plt.scatter(X[50:, 0], X[50:, 1], color='red', marker='x', label='Negative')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend(loc = 'upper left')
plt.title('Normalization data')
plt.show()
# 直线初始化
# X加上偏置项
X = np.hstack((np.ones((X.shape[0],1)), X))
# 权重初始化
w = np.random.randn(3,1)
for i in range(100):
s = np.dot(X, w)
y_pred = np.ones_like(y)
loc_n = np.where(s < 0)[0]
y_pred[loc_n] = -1
num_fault = len(np.where(y != y_pred)[0])
print('第%2d次更新,分类错误的点个数:%2d' % (i, num_fault))
if num_fault == 0:
break
else:
t = np.where(y != y_pred)[0][0]
w += y[t] * X[t, :].reshape((3,1))
# 直线第一个坐标(x1,y1)
x1 = -2
y1 = -1 / w[2] * (w[0] * 1 + w[1] * x1)
# 直线第二个坐标(x2,y2)
x2 = 2
y2 = -1 / w[2] * (w[0] * 1 + w[1] * x2)
# 作图
plt.scatter(X[:50, 1], X[:50, 2], color='blue', marker='o', label='Positive')
plt.scatter(X[50:, 1], X[50:, 2], color='red', marker='x', label='Negative')
plt.plot([x1,x2], [y1,y2],'r')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend(loc = 'upper left')
plt.show()