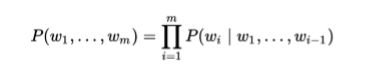NLP常见语言模型总结
目录
一、词的离散表示
1、One-hot编码(独热编码)
2、Bag of Words(BOW,词袋模型)
3、N-gram语言模型
二、词的分布式表示(Distributed Representation)
1、共现矩阵(Co-currence Matrix)
2、神经网络语言模型(Neural Network Language Model,NNLM)
3、Word2Vec,GloVe,Doc2Vec,Fasttext,Elmo,Bert,Flair
一、词的离散表示
语料库:(1)John likes to watch movies. Mary likes too. (2)John also likes to watch football games.
字典: {"John": 1, "likes": 2, "to": 3, "watch": 4, "movies": 5, "also": 6, "football": 7, "games": 8, "Mary": 9, "too": 10}
字典包含10个单词,每个单词有唯一索引;在词典中的顺序和在句子中的顺序没有关联
1、One-hot编码(独热编码)
One-Hot编码是分类变量作为二进制向量的表示。这首先要求将分类值映射到整数值。然后,每个整数值被表示为二进制向量,除了整数的索引之外,其它都是零值,它被标记为1。
使用one-hot编码,将离散特征的取值扩展到了欧式空间,离散特征的某个取值就对应欧式空间的某个点
John: [1, 0, 0, 0, 0, 0, 0, 0, 0, 0] ;likes: [0, 1, 0, 0, 0, 0, 0, 0, 0, 0];……too : [0, 0, 0, 0, 0, 0, 0, 0, 0, 1]
from sklearn.preprocessing import OneHotEncoder2、Bag of Words(BOW,词袋模型)
BOW模型忽略了文本的语法和语序,用一组无序的单词(words)来表达一段文字或一个文档。(文档的向量表示可以直接将各词的词向量加和表示)
John likes to watch movies. Mary likes too. 表示为:[1, 2, 1, 1, 1, 0, 0, 0, 1, 1]
John also likes to watch football games. 表示为:[1, 1, 1, 1, 0, 1, 1, 1, 0, 0]
这两个向量共包含10个元素, 其中第i个元素表示字典中第i个单词在句子中出现的次数. 因此BOW模型可认为是一种统计直方图 (histogram)。在文本检索和处理应用中, 可以通过该模型很方便的计算词频。
from sklearn.feature_extraction.text import CountVectorizer缺陷:“词汇鸿沟”现象,稀疏方式存储,其独立性假设不太符合语言文字实际分布情况,忽略了单词间的语法和顺序,无法了解单词间的关联程度。
解决:采用高阶(2阶以上)统计语言模型:Bi-Gram、Tri-Gram等。
3、N-gram语言模型
N-gram是计算机语言学和概率论范畴内的概念,是指给定的一段文本或语音中N个项目(item)的序列。项目(item)可以是音节、字母、单词或碱基对。通常N-grams取自文本或语料库。
N=1时称为unigram,N=2称为bigram,N=3称为trigram,以此类推。
(1)N-gram原理
N-Gram是基于一个假设:第n个词出现与前n-1个词相关,而与其他任何词不相关。(这也是隐马尔可夫当中的假设。)整个句子出现的概率就等于各个词出现的概率乘积。各个词的概率可以通过语料中统计计算得到。
假设句子T是有词序列w1,w2,w3...wn组成,用公式表示N-Gram语言模型如下:
P(T)=P(w1)*p(w2)*p(w3)***p(wn)=p(w1)*p(w2|w1)*p(w3|w1w2)***p(wn|w1w2w3...)
一般常用的N-Gram模型是Bi-Gram和Tri-Gram。分别用公式表示如下:
Bi-Gram: P(T)=p(w1|begin)*p(w2|w1)*p(w3|w2)***p(wn|wn-1)
Tri-Gram: P(T)=p(w1|begin1,begin2)*p(w2|w1,begin1)*p(w3|w2w1)***p(wn|wn-1,wn-2)
注意上面概率的计算方法:P(w1|begin)=以w1为开头的所有句子/句子总数;p(w2|w1)=w1,w2同时出现的次数/w1出现的次数。以此类推。
(2)N-gram语言模型学习(可参看统计自然语言处理)
N-gram语言模型 N-gram语言模型
为2-gram建立索引:{"John likes”: 1, "likes to”: 2, "to watch”: 3, "watch movies”: 4, "Mary likes”: 5, "likes too”: 6, "John also”: 7, "also likes”: 8, “watch football”: 9, "football games": 10}
John likes to watch movies. Mary likes too. 表示为:[1, 1, 1, 1, 1,1, 0, 0, 0, 0]
John also likes to watch football games. 表示为:[0, 1, 1, 0, 0, 0, 1, 1,1, 1]
模型参数数量与n的关系如下表
| n | 模型参数数量 |
| 1(unigram) |
|
| 2(Bi-gram) | |
| 3(Tri-gram) | |
| 4(4-gram) |
一句话(词组合)出现的概率
Unigram/1-gram :P(Mary likes too) = P(too | Mark, likes) * P(likes | Mary) * P(Mary) = P(too) * P(likes) * P(Mary)
Bi-gram/2-gram :P(Mary likes too) = P(too | Mark, likes) * P(likes | Mary) * P(Mary) = P(too | likes) * P(likes | Marry) * P(Mary)
注意(One-hot,BOW,n-gram)离散表示的问题:
无法衡量词向量之间的关系;词表维度随着语料库增长而膨胀;n-gram语言模型考虑了词的顺序,但是 n-gram词序列随语料库膨胀的更快;数据稀疏问题等。
可以使用KenLm这个工具训练统计n-gram语言模型。
二、词的分布式表示(Distributed Representation)
词的分布式表示核心是:上下文的表示以及上下文与目标词之间的关系的建模。
1、共现矩阵(Co-currence Matrix)
基于矩阵的分布表示主要是构建“词-上下文”矩阵,通过某种技术从该矩阵中获取词的分布表示。矩阵的行表示词,列表示上下文,每个元素表示某个词和上下文共现的次数,这样矩阵的一行就描述了该词的上下文分布。
常见的上下文有:(1)文档,即“词-文档”矩阵;(2)上下文的每个词,即“词-词”矩阵;(3)n-元词组,即“词-n-元组”矩阵。
经典模型代表:Global Vector模型(GloVe)是一种对“词-词”矩阵进行分解从而得到词表示的方法。
GloVe模型(Global Vectors for Word Representation)
(1)共现矩阵的表示
词-文档(Word-Document)的共现矩阵主要用于发现主题(topic),用于主题模型,如LSA(Latent Semantic Analysis)。
词-词(Word-Word)共现矩阵可以挖掘语法和语义信息。
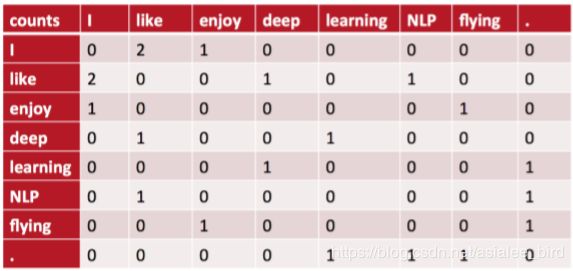
例如:语料库如下:
• I like deep learning.
• I like NLP.
• I enjoy flying.
则共现矩阵表示如下:(使用对称的窗函数(左右window length都为1) )
例如:“I like”出现在第1,2句话中,一共出现2次,所以= 2; 对称的窗口指的是,“like I”也是2次。
将共现矩阵行(列)作为词向量表示后,可以知道like,enjoy都是在I附近且统计数目大约相等,他们意思相
(2)共现矩阵表示存在的问题
将共现矩阵的行列作为词向量:向量维数随着词典大小线性增长;存储整个词典的空间消耗非常大;一些模型如文本分类模型会面临稀疏问题;模型会欠稳定。
解决办法:构造低维稠密向量作为词的分布式表示(25~1000维),如使用奇异值分解SVD(Singular Value Decomposition)对共现矩阵向量做降维。
2、神经网络语言模型(Neural Network Language Model,NNLM)
3、Word2Vec,GloVe,Doc2Vec,Fasttext,Elmo,Bert,Flair
详见:NLP词向量和句向量方法总结及实现