机器学习笔记 softmax的实现 ex4Data数据集

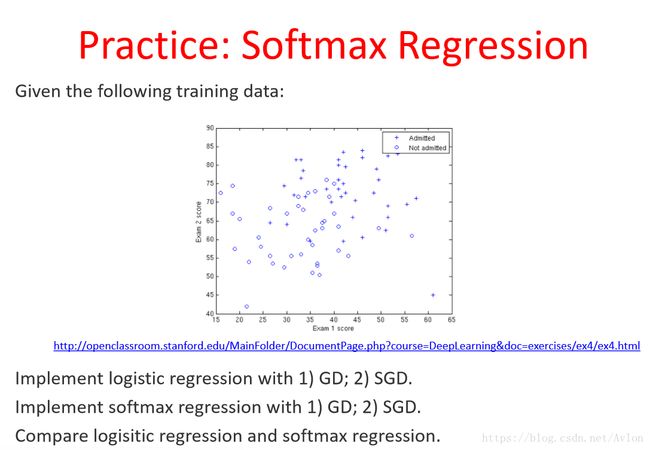
ML课的第三个练习作业

总共实现两个优化算法一个是GD一个是SGD，逻辑回归的已经在前面的博客中实现过了

数据集链接：

http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearning&doc=exercises/ex4/ex4.html

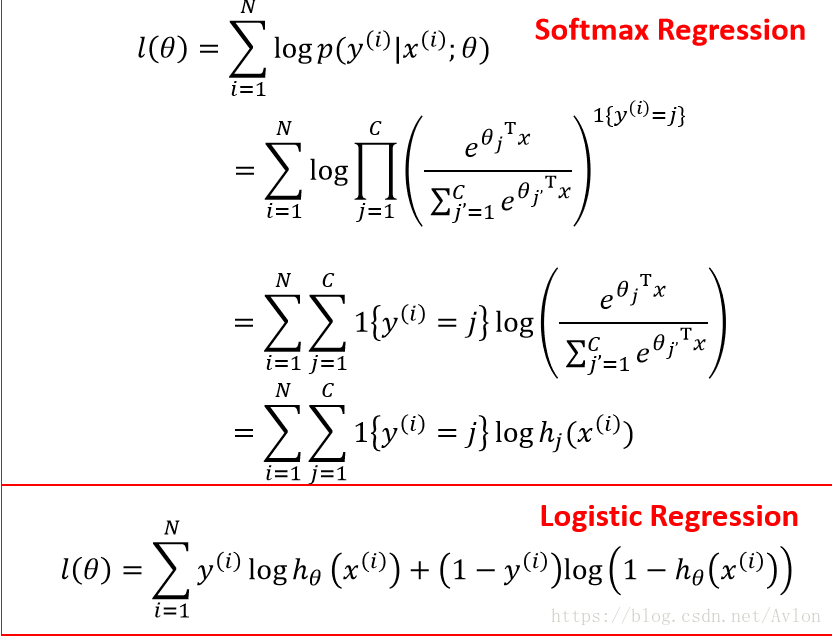
softmax的模型实际就是一个相对概率模型，公式如下：

θj就是对应于第j类的参数，θc=0可以理解为我们实际上是在分类C-1个类，第C个类是剩下的，其实在实际操作中不强制等于0也可以，后面我们将看到结果。

和逻辑回归一样我们的loss函数是对θ做最大似然估计：

对loss函数求导得到梯度，因为最大似然估计要求最大化似然函数，所以参数更新是+上梯度。

上式可以看出，当预测类别和实际类比一致时，求和项取正值，其余类别都是负值，优化方向是使整个和最大，则随着优化的进行正值项变大，负值项趋于0，预测准确率便不断提高。

更新公式如下：

 

首先给出梯度下降的代码，首先在其他文件里定义了一个获得loss值的函数，这样代码结构会清晰一些

def get_loss(x, y, w):
    temps = np.exp(x*w)
    temps = temps/np.sum(temps, axis=1)
    temps = np.log(temps)
    temps = np.array(temps)
    cast = 0
    for j in range(y.size):
        cast += temps[j][int(y[j])]
    return cast

 

由于数据集和逻辑回归一样，所以可视化部分就直接借用了前面的程序：

import numpy as np
import matplotlib.pyplot as plt
import nolinear as nl

data_x = np.loadtxt("ex4Data/ex4x.dat")
data_y = np.loadtxt("ex4Data/ex4y.dat")
plt.axis([15, 65, 40, 90])
plt.xlabel("exam 1 score")
plt.ylabel("exam 2 score")
for i in range(data_y.size):
    if data_y[i] == 1:
        plt.plot(data_x[i][0], data_x[i][1], 'b+')
    else:
        plt.plot(data_x[i][0], data_x[i][1], 'bo')
mean = data_x.mean(axis=0)
variance = data_x.std(axis=0)
data_x = (data_x-mean)/variance
data_y = data_y.reshape(-1, 1)          # 拼接
temp = np.ones(data_y.size)
data_x = np.c_[temp, data_x]
data_x = np.mat(data_x)

learn_rate = 0.1
theta = np.mat(np.zeros([3, 2]))
const = np.array(np.zeros([data_y.size, 2]))

for i in range(data_y.size):
    const[i][int(data_y[i])] = 1

loss = 0
old_loss = 0
loss = nl.get_loss(data_x, data_y, theta)

while abs(old_loss-loss) > 0.001:
    temp = np.exp(data_x*theta)
    temp = temp / np.sum(temp, axis=1)
    temps = np.mat(const-temp)
    theta = theta + learn_rate*(temps.T*data_x).T
    old_loss = loss
    loss = nl.get_loss(data_x, data_y, theta)
    print(old_loss)

theta = np.array(theta)
print(theta)
plot_y = np.zeros(65-16)
plot_x = np.arange(16, 65)
for i in range(16, 65):
    plot_y[i - 16] = -(theta[0][1] + theta[2][1] * ((i - mean[0]) / variance[0])) / theta[1][1]
    plot_y[i - 16] = plot_y[i - 16] * variance[1] + mean[1]
plt.plot(plot_x, plot_y)
plt.show()

 

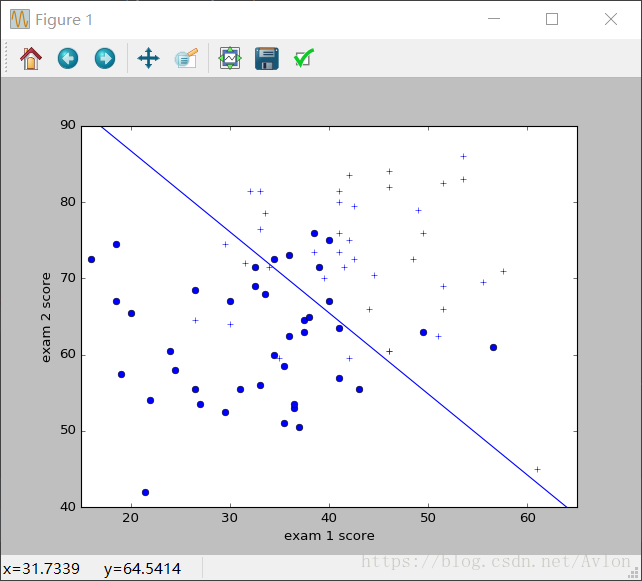
分类结果：

参数值：

可以看到θ1和θ2是一样的，实际上在上面的严格公式中我们强制要求θ2为0，很明显二分类只需要一条直线，而N分类只需要N-1条直线便是N-1组参数，用θ2画出的直线和上图一致。

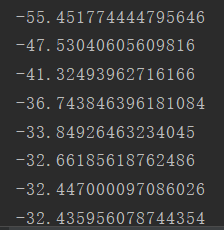
loss值的变化：

SGD每次随机抽取一个数据做梯度下降，在GD的代码上稍作修改即可实现，直接给出代码：

import numpy as np
import matplotlib.pyplot as plt
import nolinear as nl
import random

data_x = np.loadtxt("ex4Data/ex4x.dat")
data_y = np.loadtxt("ex4Data/ex4y.dat")
plt.axis([15, 65, 40, 90])
plt.xlabel("exam 1 score")
plt.ylabel("exam 2 score")
for i in range(data_y.size):
    if data_y[i] == 1:
        plt.plot(data_x[i][0], data_x[i][1], 'b+')
    else:
        plt.plot(data_x[i][0], data_x[i][1], 'bo')
mean = data_x.mean(axis=0)
variance = data_x.std(axis=0)
data_x = (data_x-mean)/variance
data_y = data_y.reshape(-1, 1)          # 拼接
temp = np.ones(data_y.size)
data_x = np.c_[temp, data_x]
data_x = np.mat(data_x)

learn_rate = 0.1
theta = np.mat(np.zeros([3, 2]))
const = np.array(np.zeros([data_y.size, 2]))

for i in range(data_y.size):
    const[i][int(data_y[i])] = 1

loss = 0
old_loss = 0
loss = nl.get_loss(data_x, data_y, theta)

while abs(old_loss-loss) > 0.001:
    temp = np.exp(data_x*theta)
    temp = temp / np.sum(temp, axis=1)
    temps = np.mat(const-temp)
    z = random.randint(0, data_y.size-1)
    x = data_x[z]
    temps = temps[z]
    theta = theta + learn_rate*(temps.T*x).T
    old_loss = loss
    loss = nl.get_loss(data_x, data_y, theta)
    print(old_loss)

theta = np.array(theta)
print(theta)
plot_y = np.zeros(65-16)
plot_x = np.arange(16, 65)
for i in range(16, 65):
    plot_y[i - 16] = -(theta[0][1] + theta[2][1] * ((i - mean[0]) / variance[0])) / theta[1][1]
    plot_y[i - 16] = plot_y[i - 16] * variance[1] + mean[1]
plt.plot(plot_x, plot_y)
plt.show()

SGD每次一个样本使得训练结果有一定的随机性

loss的最后收敛至-32