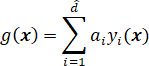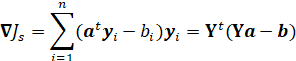机器学习：梯度下降和牛顿法
一、问题描述
考虑将基本梯度下降和牛顿法应用到表中的数据上。
(a)用这两种算法对二维数据给出
和
的判别。对梯度下降法取
。画出以迭代次数为准则函数的曲线。
(b)估计这两种方法的数学运算量。
(c)画出收敛时间-学习率曲线。求出无法收敛的最小学习率。
二、算法核心思想分析
1、线性判别函数
由
的各个分量的线性组合而成的函数：
这里
是“权向量”，
被称为“阈值权”。对于二分类器来说，若
，则判定为
，若
，则判定为
。方程
定义了一个判定面，把两个类分开，被称为“超平面”。
2、广义线性判别函数
线性判别函数
可写成：
其中系数
是权向量
的分量。通过加入另外的项（
的各对向量之间的乘积），我们得到二次判别函数：
因为
，不失一般性我们可以假设
。由此，二次判别函数拥有更多系数来产生复杂的分隔面。此时
定义的分隔面试一个二阶曲面或说是“超二次曲面”。
若继续加入更高次的项，我们就得到多项式判别函数。这可看做对某一判别函数
做级数展开，然后取其截尾逼近，此时广义线性判别函数可写成：
或
这里
通常被称为“增广特征向量”，类似地，
被称为“增广权向量”，设
，可写成：
对于两类线性可分的情况，使用判别函数
来划分
和
，若
，则判定为
，若
，则判定为
。
通常引入边界裕量
限制解区域，要求解向量满足：
3、梯度下降
我们在寻找满足线性不等式组
的解时所采用的方法是：定义一个准则函数
，当
是解向量时，
为最小。这样就将问题简化为一个标量函数的极小化问题——通常可用梯度下降法来解决。梯度下降的原理非常简单，首先从一个任意选择的权向量
开始，计算其梯度向量 
，下一个值
由自
向下降最陡的方向移一段距离而得到，即沿梯度的负方向。通常
由等式
计算，
是正的比例因子，或者说是用于设定步长的“学习率”（learning rate）。我们希望得到这样一个权向量序列：最终收敛到一个使
极小化的解上。
步骤：初始化权向量
、阈值
和学习率
，不断迭代更新
，直到
，使得准则函数达到一个极小值，
收敛。
4、牛顿法
牛顿法权向量的更新公式为：
其中，
为准则函数的赫森矩阵。收敛条件为：
因为牛顿法使用了准则函数的二次偏导，因此牛顿法比梯度下降每一步都给出了更好的步长，也就更快收敛。但是每次递归都要计算赫森矩阵
的逆，时间复杂度为
，运算量更大。
三、题目分析
1、题目分析
本题表格中给出用于求判别函数中解向量的数据，二维数据
、
共20组。需要假设用于判别的准则函数，使用梯度下降算法和牛顿法分别与准则函数结合，求出解向量，从而求得线性判别函数。并画出以迭代次数为准则函数的曲线。
本题中假设准则函数为：
梯度如下：
其中
为解向量，
为训练数据，
为边界裕量。
2、梯度下降
使用LMS算法进行迭代。学习率设为0.001，阈值设为0.01，沿负梯度方向更新权值，最后画出【迭代次数-准则函数曲线】、【分类界面】、【学习率-迭代次数曲线】，并得出无法收敛的最小学习率。
3、牛顿法
黑塞矩阵H由准则函数的二阶偏导求得，为
，代入样本计算即可，将其求逆并与梯度相乘，更新权重。最后画出【迭代次数-准则函数曲线】和【分类界面】。
4、Notice：
- 学习率
的选择对于梯度下降算法收敛至关重要。如果
太小，收敛将非常慢；如果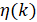
太大的话可能会过冲（overshoot），甚至发散。 - 对于数据的使用需要注意，不是直接利用原始数据进行训练，而是将原始数据增加一列，将其变成增广矩阵。
- 边界裕量
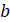的取值任意 - 牛顿法中学习率为
，所以需要赫森矩阵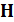
是非奇异矩阵。
四、代码及运行结果
1、梯度下降
# -*- coding:utf-8 -*-
import xlrd
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 读取数据
def read_data():
x = []
data = xlrd.open_workbook("lab4_data.xlsx")
table = data.sheets()[0]
rows = table.nrows
for i in range(1, rows):
row_value = table.row_values(i)
if row_value[2] == 1 or row_value[2] == 3:
x.append(row_value)
return x
# 准则函数
def get_j(a, b, y):
j = 0.5 * np.power(np.linalg.norm((y * a - b)), 2)
print("j", j)
return j
# 准则函数的梯度
def get_gradient(a, b, y):
gradient = y.T * (y * a - b)
print("gradient", np.shape(gradient), "\n", gradient)
return gradient
# 权向量的变化
def get_delta(eta, a, b, y):
gradient = get_gradient(a, b, y)
delta = eta * gradient
print("delta", np.shape(delta), "\n", delta)
return delta
# 解向量
def get_a(a_k, delta):
a = a_k - delta
print("a", np.shape(a), "\n", a)
return a
# 线性判别函数
def get_gx(a, y):
gx = a.T * y
return gx
# 梯度下降：传入学习率，返回收敛时间、准则函数
def gradient_decent(eta, a, b, y, theta):
iteration = []
J = []
count = 0
loop_max = 100
j = get_j(a, b, y)
print("(", count, j, ")")
iteration.append(count)
J.append(j)
delta = get_delta(eta, a, b, y)
while np.linalg.norm(delta) >= theta:
count += 1
if count >= loop_max:
print("break!")
break
delta = get_delta(eta, a, b, y)
a = get_a(a, delta) # 更新a
j = get_j(a, b, y)
iteration.append(count)
J.append(j)
print("(", count, j, ")")
return iteration, J
def main():
data = read_data()
# print("data\n", np.mat(data))
w = [x[:2] for x in filter(lambda x: x, data)]
y = list(map(lambda x: [1, *x], w))
# print("y\n", np.mat(y))
# 规范化
w1 = [x[:2] for x in filter(lambda x: x[2] == 1, data)]
w3 = [x[:2] for x in filter(lambda x: x[2] == 3, data)]
test = []
for i in range(len(w1)):
w1[i].insert(0, 1)
test.append(w1[i])
# w3 = (-1 * np.mat(w3)).tolist()
for i in range(len(w3)):
w3[i].insert(0, -1)
test.append(w3[i])
print(np.mat(test))
y = test
# initial
a = [1, 1, 1] # 权向量a
theta = 0.01 # 阈值θ
eta = 0.001 # 学习率η
b = [1 for i in range(len(y))] # 边界裕量
y = np.mat(y)
a = np.mat(a).T
b = np.mat(b).T
print("y", np.shape(y), "\n", y)
print("a", np.shape(a), "\n", a)
print("b", np.shape(b)) # , "\n", b
# Gradient Decent
fig1 = plt.figure(1)
iteration, J = gradient_decent(eta, a, b, y, theta)
plt.plot(iteration, J) # 准则函数
plt.title(u"学习率η = " + str(eta))
plt.xlabel(u"迭代次数")
plt.ylabel(u"准则函数")
# 绘制样本点
fig2 = plt.figure(2)
w1 = [x[:2] for x in filter(lambda x: x[2] == 1, data)]
w3 = [x[:2] for x in filter(lambda x: x[2] == 3, data)]
w1x1 = [x[0] for x in filter(lambda x: x, w1)]
w1x2 = [x[1] for x in filter(lambda x: x, w1)]
w3x1 = [x[0] for x in filter(lambda x: x, w3)]
w3x2 = [x[1] for x in filter(lambda x: x, w3)]
plt.scatter(w1x1, w1x2, c='r')
plt.scatter(w3x1, w3x2, c='g')
plt.xlabel("x1")
plt.ylabel("x2")
plt.title(u"分类界面")
# # 准则函数分隔面
x = [np.linspace(-5.1, 6.8, 100)] # [1 for i in range(len(y))],
x = np.mat(x).T
x2 = (a[0, 0] + a[1, 0] * x) / a[2, 0]
plt.plot(x, x2)
# 学习率-收敛时间
fig3 = plt.figure(3)
learn_rate = [0.0005, 0.001, 0.0015, 0.002, 0.0025, 0.003, 0.0035, 0.004, 0.0045, 0.005, 0.0055]
convergence = []
for i in range(len(learn_rate)):
iteration, J = gradient_decent(learn_rate[i], a, b, y, theta)
convergence.append(iteration[-1])
print(learn_rate, "\n", convergence)
plt.plot(learn_rate, convergence)
for xy in zip(learn_rate, convergence):
plt.annotate("(%s,%s)" % xy, xy=xy, xytext=(-20, 10), textcoords='offset points')
plt.xlabel(u"学习率")
plt.ylabel(u"收敛时间")
plt.title(u"学习率-收敛时间")
plt.show()
if __name__ == '__main__':
main()
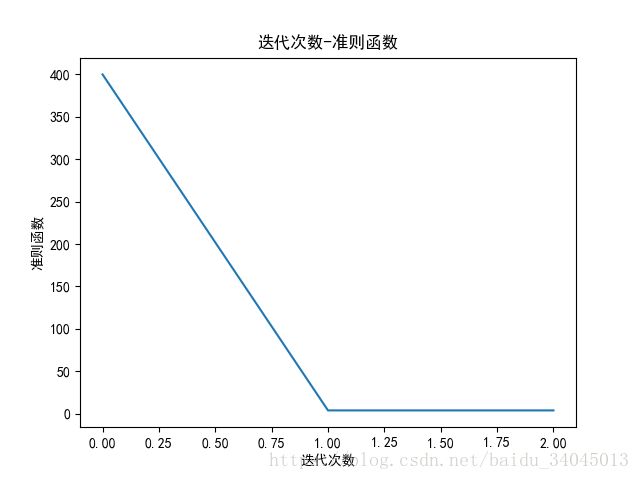
【迭代次数-准则函数曲线】
学习率为0.001时，在所设阈值下，梯度下降16次收敛
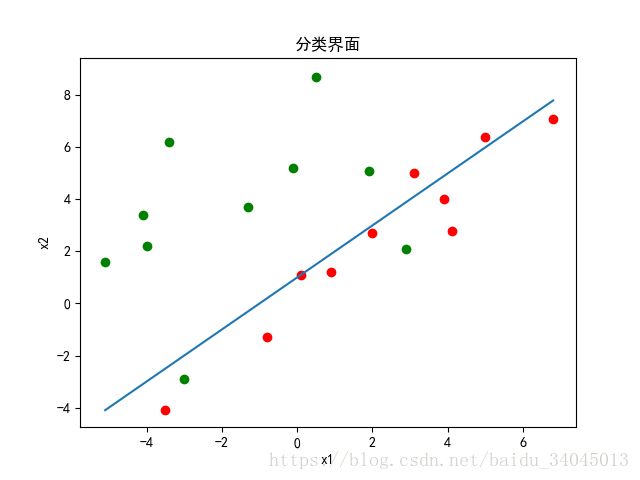
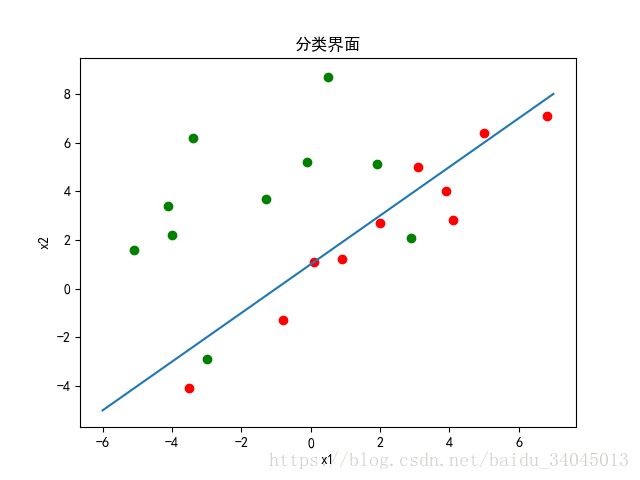
【分类界面】
权向量为[ 0.73775053 -0.19529194 0.23079494 ]
可以看到LMS算法并未给出最优解
【学习率-迭代次数曲线】
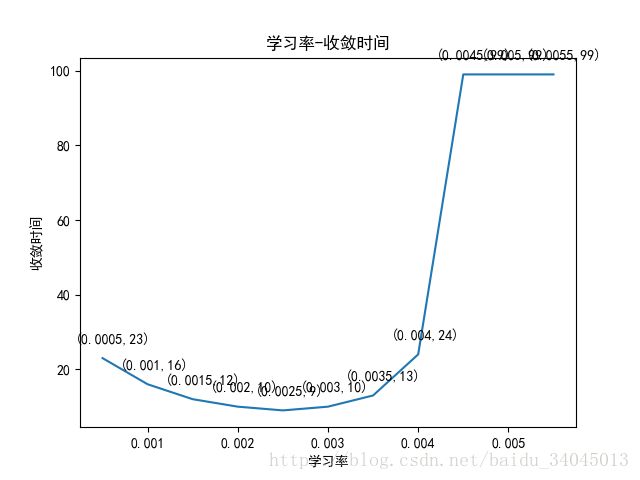
当学习率达到0.0045左右时，梯度下降无法收敛
2、牛顿法
# -*- coding:utf-8 -*-
import xlrd
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 读取数据
def read_data():
x = []
data = xlrd.open_workbook("lab4_data.xlsx")
table = data.sheets()[0]
rows = table.nrows
for i in range(1, rows):
row_value = table.row_values(i)
if row_value[2] == 1 or row_value[2] == 3:
x.append(row_value)
return x
# 准则函数
def get_j(a, b, y):
j = 0.5 * np.power(np.linalg.norm((y * a - b)), 2)
print("j", j)
return j
# 准则函数的梯度
def get_gradient(a, b, y):
gradient = y.T * (y * a - b)
print("gradient", np.shape(gradient), "\n", gradient)
return gradient
# 权向量的变化
def get_delta(H, a, b, y):
gradient = get_gradient(a, b, y)
delta = H * gradient
print("delta", np.shape(delta), "\n", delta)
return delta
# 解向量
def get_a(a_k, delta):
a = a_k - delta
print("a", np.shape(a), "\n", a)
return a
# 线性判别函数
def get_gx(a, y):
gx = a.T * y
return gx
def newton(H, a, b, y, theta):
iteration = []
J = []
count = 0
loop_max = 100
j = get_j(a, b, y)
print("(", count, j, ")")
iteration.append(count)
J.append(j)
delta = get_delta(H, a, b, y)
while np.linalg.norm(delta) >= theta:
count += 1
if count >= loop_max:
print("break!")
break
delta = get_delta(H, a, b, y)
a = get_a(a, delta) # 更新a
j = get_j(a, b, y)
iteration.append(count)
J.append(j)
print("(", count, j, ")")
return iteration, J
def main():
data = read_data()
# print("data\n", np.mat(data))
w = [x[:2] for x in filter(lambda x: x, data)]
y = list(map(lambda x: [1, *x], w))
# print("y\n", np.mat(y))
# 规范化
w1 = [x[:2] for x in filter(lambda x: x[2] == 1, data)]
w3 = [x[:2] for x in filter(lambda x: x[2] == 3, data)]
test = []
for i in range(len(w1)):
w1[i].insert(0, 1)
test.append(w1[i])
# w3 = (-1 * np.mat(w3)).tolist()
for i in range(len(w3)):
w3[i].insert(0, -1)
test.append(w3[i])
print(np.mat(test))
y = test
# initial
a = [1, 1, 1] # 权向量a
theta = 0.001 # 阈值θ
H = 0 # 学习率 黑塞矩阵的逆
b = [1 for i in range(len(y))] # 边界裕量
y = np.mat(y)
a = np.mat(a).T
b = np.mat(b).T
print("y", np.shape(y), "\n", y)
print("a", np.shape(a), "\n", a)
print("b", np.shape(b)) # , "\n", b
H = (y.T * y).I
print("H", H)
fig1 = plt.figure(1)
iteration, J = newton(H, a, b, y, theta)
plt.plot(iteration, J) # 准则函数
plt.xlabel(u"迭代次数")
plt.ylabel(u"准则函数")
plt.title(u"迭代次数-准则函数")
# 绘制样本点
fig2 = plt.figure(2)
w1 = [x[:2] for x in filter(lambda x: x[2] == 1, data)]
w3 = [x[:2] for x in filter(lambda x: x[2] == 3, data)]
w1x1 = [x[0] for x in filter(lambda x: x, w1)]
w1x2 = [x[1] for x in filter(lambda x: x, w1)]
w3x1 = [x[0] for x in filter(lambda x: x, w3)]
w3x2 = [x[1] for x in filter(lambda x: x, w3)]
plt.scatter(w1x1, w1x2, c='r')
plt.scatter(w3x1, w3x2, c='g')
plt.xlabel("x1")
plt.ylabel("x2")
plt.title(u"分类界面")
# 准则函数分隔面
x = [np.linspace(-6, 7, 100)] # [1 for i in range(len(y))],
x = np.mat(x).T
x2 = (a[0, 0] + a[1, 0] * x) / a[2, 0]
plt.plot(x, x2)
plt.show()
if __name__ == '__main__':
main()
【迭代次数-准则函数曲线】
在所设阈值下，牛顿法收敛步数远小于梯度下降
【分类界面】
权向量为[ 0.39200249 -0.15039118 0.2144672 ]
牛顿法和梯度下降都是为了寻找准则函数的极小值，所以两者最后收敛结果一致，仅在算法复杂度和收敛步数有区别。
3、运算量分析
梯度下降运算量：取决于收敛的步数，即迭代的次数，学习量与迭代次数成正比。
牛顿法运算量：不仅取决于收敛的步数，同时取决于赫森矩阵H 的运算复杂度。
五、总结
基本梯度下降法和牛顿法都能求得最终的权向量，使得准则函数取得一个极小值。一般来说，即使有了最佳的η(k) ，牛顿法也比梯度下降法在每一步都给出了更好的步长，所以收敛速度更快。但是当赫森矩阵H 为奇异矩阵时就不能用牛顿法了。而且，即使H 是非奇异的，每次递归时计算H 逆矩阵所需的
时间可轻易地将牛顿法带来的好处给抵消了。实际上，将η(k) 设置为比较小的常数
，虽然比每一步都使用最优的η(k) 将需要更多步骤来校正，但通常总的时间开销却更少。
如有错误请指正