《统计学习方法》感知机学习笔记与Python实现

学习笔记

1.感知机模型

假设输入空间（特征空间）是 X⊆Rn X ⊆ R n ，输出空间是 Y={+1,−1} Y = { + 1 , − 1 } 。输入 x∈X x ∈ X 表示示例的特征向量，对应于输如入空间的点；输出 y∈Y y ∈ Y 表示示例的类别。由输入空间到输出空间的如下函数

f(x)=sign(w⋅x+b f ( x ) = sign ( w ⋅ x + b

成为感知机。其中， w w 和 b b 为感知机模型参数， w∈Rn w ∈ R n 叫作权重（weight）或权值向量（weight vector）， b∈R b ∈ R 叫作偏置（bias）， w⋅x w ⋅ x 表示 w w 和 x x 的内积。sign是符号函数，即

sign(x)={+1,−1,x≥0x<0 sign ( x ) = { + 1 , x ≥ 0 − 1 , x < 0

感知机是一种线性分类模型，属于判别模型。
线性方程 w⋅x+b=0 w ⋅ x + b = 0 对应于特征空间 Rn R n 中的超平面 S S ,其中 w w 是超平面的法向量， b b 是超平面的截距。这个超平面将特征空间划分为两部分，位于两部分的点分别被分为正类和负类。超平面 S S 也被称为分离超平面。

2.感知机学习策略

为确定感知机模型的参数 w w 和 b b ，需要确定一个学习策略，即定义损失函数并将损失函数极小化。感知机学习的策略是在假设空间中选取使损失函数最小的模型参数 w w 和 b b 。在这里，感知机所采用的损失函数是误分类点到超平面 S S 的总距离。
给定一个线性可分的训练集

T={(x1,y1),(x2,y2),...(xN,yN)} T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . ( x N , y N ) }

其中， xi∈X=Rn,y∈Y={+1,−1},i=1,2,…,N x i ∈ X = R n , y ∈ Y = { + 1 , − 1 } , i = 1 , 2 , … , N
在输入空间 Rn R n 中任意一点 x0 x 0 到超平面是的距离是：

1∥w∥|w⋅x0+b| 1 ‖ w ‖ | w ⋅ x 0 + b |

对误分类数据 (xi,yi)，有： ( x i , y i ) ， 有 ： −yi(w⋅xi+b)>0 − y i ( w ⋅ x i + b ) > 0 $

假设误分类点集合为 M M ，则所有误分类点到超平面的总距离为：

−1∥w∥∑xi∈Myi(w⋅xi+b) − 1 ‖ w ‖ ∑ x i ∈ M y i ( w ⋅ x i + b )

不考虑 1∥w∥ 1 ‖ w ‖ , 即可得到感知机学习的损失函数

L(w,b)=−∑xi∈Myi(w⋅xi+b) L ( w , b ) = − ∑ x i ∈ M y i ( w ⋅ x i + b )

显然，损失函数 L(w,b) L ( w , b ) 是非负的。如果没有误分类点，损失函数值为0，而且，误分类点越少，误分类点离超平面越近，损失函数的值越小。

3.感知机学习算法

求解 w,b w , b ，即求解最优化问题

minw,bL(w,b)=−∑xi∈Myi(w⋅xi+b) min w , b L ( w , b ) = − ∑ x i ∈ M y i ( w ⋅ x i + b )

感知机学习算法是误分类驱动的，具体采用随机梯度下降法。首先，任意选取一个超平面 w0 w 0 , b0 b 0 ，然后用梯度下降法不断地极小化损失函数。极小化过程中不是一次使M中所有误分类点的梯度下降，而是一次随机选取一个误分类点使其梯度下降。损失函数 L(w,b) L ( w , b ) 的梯度为

∇wL(w,b)=−∑xi∈Myixi ∇ w L ( w , b ) = − ∑ x i ∈ M y i x i

∇bL(w,b)=−∑xi∈Myi ∇ b L ( w , b ) = − ∑ x i ∈ M y i

随机选取误分类点 (xi,yi) ( x i , y i ) ，对 w,b w , b 进行更新：

w←w+ηyixi w ← w + η y i x i

b←b+ηyi b ← b + η y i

式中 η(0<η≤1) η ( 0 < η ≤ 1 ) 是步长（在统计学习中又称学习率）。通过迭代可以期待损失函数不断减小，直到为0。

感知机学习算法的原始形式
输入：训练集T = { (x_1,y_1),(x_2,y_2),\ldots,(x_N,y_N)}, 其中 xi∈X=Rn,yi∈Y,i=1,2,…,N x i ∈ X = R n , y i ∈ Y , i = 1 , 2 , … , N ；学习率 η(0<η≤1) η ( 0 < η ≤ 1 ) ；
输出： w,b w , b ；感知机模型 f(x)=sign(w⋅x+b) f ( x ) = sign ( w ⋅ x + b )
（1）选取初值 w0,b0 w 0 , b 0 ；
（2）在训练集中选取数据 (xi,yi) ( x i , y i ) ；
（3）如果 yi(w⋅xi+b)≤0 y i ( w ⋅ x i + b ) ≤ 0

w←w+ηyixi w ← w + η y i x i

b←b+ηyi b ← b + η y i

（4）转至（2），直到训练集中没有误分类点。

例子: 正实例点： x1=(3,3)T,x2=(4,3)T x 1 = ( 3 , 3 ) T , x 2 = ( 4 , 3 ) T ，负实例点： x3=(1,1)T x 3 = ( 1 , 1 ) T ，使用感知机学习算法求解感知机模型 f(x)=sign(w⋅x+b) f ( x ) = sign ( w ⋅ x + b )

python实现感知机学习算法的原始形式

import random
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

def preception_train(X, y, lr = 1):
    X_size = X.shape[0] #训练集大小
    w = np.zeros([X.shape[1],1]) #初始化w
    b = 0 #初始化b
    iter_count = 0 #迭代次数
    print('迭代次数\t误分类点\t\tw\t\tb')
    while(True):
        cnt = 0 #已处理点的数量 
        for i in range(X_size):
            if y[i]*(np.dot(w.T,X[i])+b)<=0: # 误分类点
                #更新w和b
                w += lr*y[i]*X[i].reshape(w.shape)
                b += lr*y[i]
                print(iter_count+1,'\t\t','x'+str(i+1),'\t\t',w.T, '\t\t', b)
                iter_count+=1
                break
            cnt+=1
        if cnt == X_size:
            break
    return w,b

def plot_points(X, y, w, b):
    # 绘制图像
    plt.figure()
    x1 = np.linspace(0, 6, 100)
    x2 = (-b - w[0]*x1)/w[1]
    plt.plot(x1, x2,color='r',)
    for i in range(len(X)):
        if (y[i] == 1):
            plt.scatter(X[i][0],X[i][1],marker='o',color='g',s = 50)
        else:
            plt.scatter(X[i][0],X[i][1],marker='x',color='b',s = 50)

if __name__ == '__main__':
    X = [[3,3],[4,3],[1,1]]  
    X = np.array(X)
    y = [1,1,-1]
    y = np.array(y)
    lr = 1 #学习率
    w, b = preception_train(X,y,lr)
    plot_points(X,y,w,b)

迭代次数    误分类点        w       b
1        x1          [[ 3.  3.]]         1
2        x3          [[ 2.  2.]]         0
3        x3          [[ 1.  1.]]         -1
4        x3          [[ 0.  0.]]         -2
5        x1          [[ 3.  3.]]         -1
6        x3          [[ 2.  2.]]         -2
7        x3          [[ 1.  1.]]         -3

4.感知机学习算法的对偶形式

对偶形式的基本思想，将 w w 和 b b 表示为 xi x i 和 yi y i 的xian线性组合的形式，通过求解其系数而求得 w w 和 b b 。在原始算法中可假设初始值 w0,b0 w 0 , b 0 均为0，对误分类点 (xi,yi) ( x i , y i ) 通过

w←w+ηyixi w ← w + η y i x i

b←b+ηyi b ← b + η y i

逐步修改 w,b w , b ，设修改 ni n i 次，则 w,b w , b 关于 (xi,yi) ( x i , y i ) 的增量分别是 αiyixi α i y i x i 和 αiyi α i y i ，其中 αi=niη α i = n i η 。因此，最后学习到的 w,b w , b 可以分别表示为

w=∑i=1Nαiyixi w = ∑ i = 1 N α i y i x i

b=∑i=1Nαiyi b = ∑ i = 1 N α i y i

这里 αi≥0，i=1,2,3,.…,N α i ≥ 0 ， i = 1 , 2 , 3 , . … , N ，当 η=1 η = 1 时，表示第 i i 个实例点由于误分而进行更新的次数。
综上，可以得到 感知机学习算法的对偶形式如下：
输入：训练集T = { (x_1,y_1),(x_2,y_2),\ldots,(x_N,y_N)}, 其中 xi∈X=Rn,yi∈Y,i=1,2,…,N x i ∈ X = R n , y i ∈ Y , i = 1 , 2 , … , N ；学习率 η(0<η≤1) η ( 0 < η ≤ 1 ) ；
输出： α,b α , b ；感知机模型 f(x)=sign(∑Nj=1αjyjxj⋅x+b) f ( x ) = sign ( ∑ j = 1 N α j y j x j ⋅ x + b ) ，其中 α=(α1,α2,…,αN) α = ( α 1 , α 2 , … , α N ) 。
（1） α←0，b←0 α ← 0 ， b ← 0 ；
（2）在训练集中选取数据 (xi,yi) ( x i , y i ) ；
（3）如果 yi(∑Nj=1αjyjxj⋅xi+b)≤0 y i ( ∑ j = 1 N α j y j x j ⋅ x i + b ) ≤ 0

αi←αi+η α i ← α i + η

b←b+ηyi b ← b + η y i

（4）转至（2），直到训练集中没有误分类数据。

python实现感知机学习算法的对偶形式

import random
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

def preception_antithesis_train(X, y, lr = 1):
    X_size = X.shape[0] #训练集大小
    alpha = [0 for i in range(X_size)] #初始化w
    w = np.zeros([X.shape[1],1]) #初始化w
    b = 0 #初始化b
    gram = np.matmul(X, X.T) #计算gram矩阵

    iter_count = 0 #迭代次数
    print('迭代次数\t误分类点\talpha\t\tb')
    while(True):
        cnt = 0 #已处理点的数量 
        for i in range(X_size):
            temp = 0
            for j in range(X_size):
                temp += alpha[j]*y[j]*gram[i][j]
            temp += b
            if y[i]*temp <=0: # 误分类点
                #更新alpha[i]和b
                alpha[i] += lr
                b += lr*y[i]
                print(iter_count+1,'\t\t','x'+str(i+1),'\t\t',alpha, '\t', b)
                iter_count+=1
                break
            cnt+=1
        if cnt == X_size:
            break
    for i in range(X.shape[0]):
        for j in range(X.shape[1]):
            w[j] += alpha[i]*y[i]*X[i][j]
    return w,b

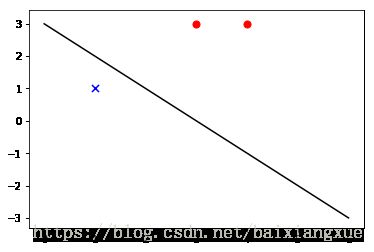
def plot_points(X, y, w, b):
    # 绘制图像
    plt.figure()
    x1 = np.linspace(0, 6, 100)
    x2 = (-b - w[0]*x1)/w[1]
    plt.plot(x1, x2,color='black',)
    for i in range(len(X)):
        if (y[i] == 1):
            plt.scatter(X[i][0],X[i][1],marker='o',color='r',s = 50)
        else:
            plt.scatter(X[i][0],X[i][1],marker='x',color='b',s = 50)

if __name__ == '__main__':
    X = [[3,3],[4,3],[1,1]]  
    X = np.array(X)
    y = [1,1,-1]
    y = np.array(y)
    lr = 1 #学习率
    w, b = preception_antithesis_train(X,y,lr)
    plot_points(X,y,w,b)

迭代次数    误分类点    alpha       b
1        x1          [1, 0, 0]   1
2        x3          [1, 0, 1]   0
3        x3          [1, 0, 2]   -1
4        x3          [1, 0, 3]   -2
5        x1          [2, 0, 3]   -1
6        x3          [2, 0, 4]   -2
7        x3          [2, 0, 5]   -3

5.感知学习算法的收敛性

当训练数据集线性可分时，感知机学习算法是收敛的。感知机算法在训练集上的误分类次数 k k 满足不等式（证明详见李航老师《统计学习方法》P31）：

k≤(Rγ) k ≤ ( R γ )

当训练数据集线性可分时，感知机学习算法存在无穷多个解，其解由于不同的初值或不同的迭代顺序而可能有所不同。

参考资料：李航 《统计学习方法》