动态规划常见题

动态规划是运筹学的一个分支，是求解决策过程最优化的数学方法。利用各个阶段之间的关系，逐个求解，最终求的全局最优解。在设计动态规划算法时，需要确认原问题与子问题、动态规划状态、边界状态的值、状态转移方程等关键要素。

爬楼梯(leetcode70)

在爬楼梯时，每次可向上走1阶台阶或2阶台阶，问有n阶楼梯有多少种上楼的方式？

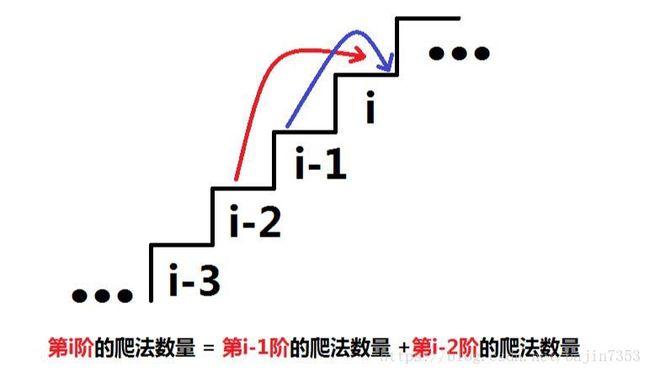
由于每次最多爬2阶，楼梯的第i阶，只可能从第i-1阶与第i-2阶到达。故到达第i阶有多少种爬法，只与第i-1、第i-2阶的爬法数量直接相关。

1设置递推数组dp[0…n],dp[i]代表到达第i阶，有多少种走法，初始化数组元素为0.
2 设置到达第1阶台阶，有1种走法；到达第2阶台阶，有2种走法。
3 利用i循环递推从第3阶至第n阶结果：
到达第i阶的方式数量 = 到达第i-1阶的方式数量+到达第i-2阶的方式数量

代码实现：

def Solution2(self,n):
    dp = []
    dp.append(0)
    dp.append(1)
    dp.append(2)
    if n >2:
        for i in range(3,n):
            dp.append(dp[i-1] +dp[i-2])
    return dp[n]

打家窃舍(leetcode198)

在一条直线上，有n个房屋，每个房屋中有数量不等的财宝，有一个盗贼希望从房屋中盗取财宝，由于房屋中有报警器，如果同时从相邻的两个房屋中盗取财宝就会触发报警器。问在不触发报警器的前提下，最多可获取多少财宝？

思考与分析：
1 n个房屋，每个房间都有盗取/不盗取两种可能，类似求子集(暴力搜索)的方法，在不触发警报的情况下，选择总和最大的子集，最多有2^n种可能，时间复杂度O(2^n),是否有更好的方法？

由于同时从相邻的两个房屋中盗取财宝就会出发报警器，故：
1 若选择第i个房间盗取财宝，就一定不能选择第I-1个房间盗取财宝
2 若不选择第i个房间盗取财宝，则相当于只考虑前I-1个房间盗取财宝。

代码实现：

def Solution(nums):
    if len(nums) == 0:
        return 0
    if len(nums) == 1:
        return nums[0]
    dp = []
    dp.append(nums[0])
    dp.append(max(nums[0],nums[1]))
    for i in range(2,len(nums)):
        dp.append(max(dp[i-1],dp[i-2]+nums[i]))
    return dp[len(nums)-1]
print(Solution([0,0]))

最大子段和(leetcode53)
给定一个数组，求这个数组的连续子数组中，最大的那一段的和

思考与分析：
对于这道题如果用暴力枚举的方法，则时间复杂度太高
用动态规划的方法重点在于确认动态规划状态。

将求n个数的数组的最大子段和，转换为分别求出以第1个，第2个、，，，第i个、，，，第n个数字结尾的最大字段和，再找出这n个结果中最大的，即为结果。

第i个状态（dp[i]）即为以第i个数字结尾的最大子段和(最优解)。由于以第I-1个数字结尾的最大子段和(dp[i-1])与nums[i]相邻：

代码实现：

def Solution(nums):
    dp = []
    dp.append(nums[0])
    max_res = dp[0]
    for i in range(1,len(nums)):

        dp.append(max(dp[i-1]+nums[i],nums[i]))
        print(dp[i])
        if max_res < dp[i]:
            max_res = dp[i]
            return max_res

array = [-1,1,2,3,1,19,1]
print(Solution(array))

找零钱(leetcode322)：

已知不同面值的钞票，求如何用最少数量的钞票组成某个金额，求可以使用的最少钞票数量。如果任意数量的已知面值钞票都无法组成该金额，则返回-1.
例如：
钞票面值：[1,2,5]金额：11 = 5+5+1 需要3张
钞票面值：[2] 金额：3 无法组成，返回-1
钞票面值：[1,2,5,7,10 金额：14 = 7+7 需要2张

思考：
利用贪心是不是可以解决这个问题？
钞票面值：[1,2,5,10];金额：14 最优解需要3张
贪心思想：每次优先使用大面值的金额，如：先选1张10块的，剩下4元，再选1张2元的，剩下2元，再选1张2元的。这就可以实现
钞票面值：[1,2,5,7,10] 金额：14 最优解需要2张(两张7块的)
这种情况下用贪心的思想来做的话，就会先选一张10块的，然后剩下4元，选了两张2块的，这就选错了！

所以：贪心思想在个别面值组合时是可以的，比如日常生活中的RMB的面值，但是这个题面值不确定，所以贪心思想不可以。

算法思路：

钞票的面值：coins = [1,2,5,7,10]; 金额：14
dp[i], 代表金额i 的最优解(即最小使用张数)
dp[]中存储金额1到金额14的最优解

在计算dp[i]时，dp[0]、dp[1]、，，，、dp[i-1]都是已知的：
而金额i可以由金额i-1与coins[0]组合
金额i-coins[k] 与coins[k]组合

即状态i可以由状态i-coins[k] k个状态所转移到。

代码实现：

def Solution(coins,amount):
    dp = []
    if amount == 0:
        return 0
    for i in range(amount+1):
        dp.append(-1)

    dp[0] = 0
    for i in range(1,amount+1):
        print(i)
        for j in range(len(coins)):
            print(coins[j])
            if (i-coins[j]) >=0 and dp[i-coins[j]] !=-1:
                if (dp[i] == -1 or dp[i]> dp[i-coins[j]]+1):
                    print(dp[i-coins[j]]+1)
                    dp[i] = (dp[i-coins[j]] +1)
    print(dp)

    return dp[amount]
# 上面的这种解法leetcode 上会超时,对于上面的动态规划进行优化
def Solution2(self,coins,amount):
    dp = [0] + [-1] * amount
    for x in range(amount):
        if dp[x] < 0:
            continue
        for c in coins:
            if x + c > amount:
                continue
            if dp[x + c] < 0 or dp[x + c] > dp[x] + 1:
                dp[x + c] = dp[x] + 1
    return dp[amount]
# 可以将问题转换为求x轴0点到坐标点amount的最短距离(每次向前进的合法距离为coins的面值)
def coinChange(self, coins, amount):
        """
        :type coins: List[int]
        :type amount: int
        :rtype: int
        """
        if amount == 0:
            return 0
        value1 = [0]
        value2 = []
        nc =  0
        visited = [False]*(amount+1)
        visited[0] = True
        while value1:
            nc += 1
            for v in value1:
                for coin in coins:
                    newval = v + coin
                    if newval == amount:
                        return nc
                    elif newval > amount:
                        continue
                    elif not visited[newval]:
                        visited[newval] = True
                        value2.append(newval)
            value1, value2 = value2, []
        return -1

三角形(leetcode120)

给定一个二维数组，其保存了一个数字三角形，求从数字三角形顶端到底端各数字和最小的路径之和，每次可以向下走相邻的两个位置。

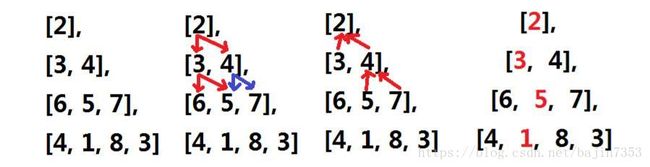
算法思路：
1 设置一个二维数组，最优值三角形dp[][],并初始化数组元素为0.dp[i][j]代表从底向上递推时，走到三角形第i行第j列的最优解。
2 从三角形的底面向三角形上方进行动态规划
动态规划边界条件：底面上的最优值即为数字三角形的最后一层。
利用i循环，从倒数第二层递推至第一层，对于每层的各列，进行动态规划递推：第i行，第j列的最优解为dp[i][j]，可到达(i,j)的两个位置的最优解dp[i+1][j],dp[i+1][j+1]:
dp[i][j] = min(dp[i+1][j],dp[i+1][j+1])+triangle[i][j]
返回dp[0][0]

代码实现：

def Solution(triangle):
    if len(triangle) ==0:
        return 0
    dp =  [[0 for i in range(len(triangle))] for i in range(len(triangle))]
    print(dp)
    for i in range(len(triangle[-1])):
        dp[-1][i] = triangle[-1][i]
    for i in range(len(triangle) - 2, -1, -1):
        for j in range(i + 1):
            dp[i][j] = min(dp[i+1][j], dp[i+1][j + 1]) + triangle[i][j]

    return dp[0][0]
if __name__ == "__main__":
    triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
    result = Solution(triangle)
    print(result)

最长上升子序列(leetcode300):
已知一个未排序数组，求这个数组最长上升子序列的长度。

思考与分析：
1 暴力枚举：n个元素组成的数组，枚举数组的全部子序列，即数组中任意某个元素都有选择、不选择两种可能，时间复杂度为O(2^n),枚举时选择最长的子序列长度最为结果。
2 采用动态规划，设第i个状态为dp[i]：第i个状态代表以第i个元素结尾的最长上升子序列的长度。
从1到n-1，循环i，计算dp[i]:
从0至i-1，循环j，若nums[i] > nums[j],说明nums[i]可放置在nums[j]的后面，组成最长上升子序列：
若dp[i] < dp[j]+1:
dp[i] = dp[j]+1
LIS为dp[0],dp[1],…dp[n-1]中最大的。

代码实现：

def Solution(self,nums):
    if len(nums) ==0:
        return 0
    dp = [0]*(len(nums)-1)
    dp[0] =1
    LIS = 1
    for i in range(1,len(dp)):
        dp[i] = 1
        for j in range(0,i):
            if nums[i] >nums[j] and dp[i] < dp[j] +1:
                dp[i] = dp[j] +1
        if LIS < dp[i]:
            LIS = dp[i]
    return LIS

最小路径和(leetcode64)：

已知一个二维数组，其中存储了非负整数，找到从左上角到右下角的一条路径，使得路径上的和最小。(移动过程中只能向下或向右)

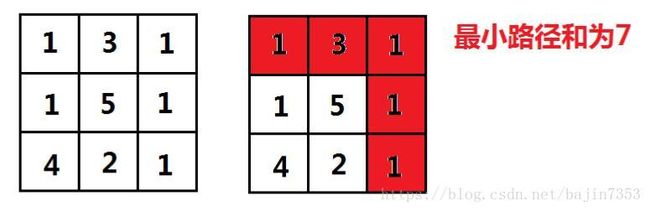
设dp[i][j]为到达位置(i,j)时的最优解(最小值)：因为只能向下或者向右走，所以dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i][j]

代码实现：

def Solution(grid):
    if not grid or len(grid) == 0:
        return 0

    dp = [[0 for i in range(len(grid[0]))] for i in range(len(grid))]
    dp[0][0] = grid[0][0]
    for i in range(1,len(grid[0])):
        dp[0][i] = dp[0][i-1]+grid[0][i]
    for i in range(1,len(grid)):
        dp[i][0] = dp[i-1][0]+grid[i][0]
        for j in range(1,len(grid[0])):
            dp[i][j] = min(dp[i-1][j],dp[i][j-1])+grid[i][j]
    return dp[-1][-1]
if __name__ == "__main__":
    grid = [[1,3,1],[1,5,1],[4,2,1]]
    result = Solution(grid)
    print(result)

地牢游戏(leetcode174):
已知一个二维数组，左上角代表骑士的位置，右下角代表公主的位置，二维数组中存储整数，正数可以给骑士增加生命值，负数会减少骑士的生命值，问骑士初始化化至少是多少生命值，才可保证骑士在行走的过程中至少保持生命值为1(骑士只能向下或向右行走)

思考与分析：
从右下向左上递推：dp[i][j]代表若要达到右下角，至少要有多少血量，能在行走的过程中至少保持生命值为1.

若代表地牢的二维数组为n*m的：
i代表行，从n-2至0：
j 代表列，从m-2至0：
设dp_min = min(dp[i+1][j],dp[i][j+1])
dp[i][j] = max(1,dp_min - dungeon[i][j])

代码实现：

def Solution(grid):
    if not grid or len(grid) == 0:
        return 0

    dp = [[0 for i in range(len(grid[0]))] for i in range(len(grid))]
    row = len(dp)
    column = len(dp[0])
    dp[-1][-1] = max(1,1-grid[-1][-1])
    for i in range(column-2,-1,-1):
        dp[-1][i] = max(1,dp[-1][i+1]-grid[-1][i])
    for i in range(row-2,-1,-1):
        dp[i][-1] = max(1,dp[i+1][-1]-grid[i][-1])
    for i in range(row-2,-1,-1):
        for j in range(column-2,-1,-1):
            dp_min = min(dp[i+1][j],dp[i][j+1])
            dp[i][j] = max(1,dp_min-grid[i][j])
    return dp[0][0]
if __name__ == "__main__":

    grid = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
    print(Solution(grid))