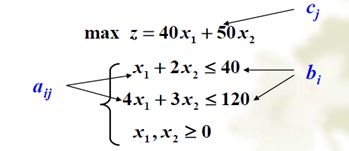线性规划中的灵敏度分析
一、 灵敏度分析介绍
线性规划模型都假定参数是已知的或确定的,然后有时候很难确切地知道这些参数,这些参数也会随着市场、技术的变化相应变化,并最终导致模型的最优解发生变化。
因此,分析参数变化对模型最优解的影响非常重要。这种分析称为灵敏度分析或what-if分析。
灵敏度分析主要有两种:目标式系数的变化和约束右端值的变化。
二、 案例
1. 问题
某陶瓷公司是一家手工艺制造公司,生产陶制的碗和杯子,使用两大主要资源是粘土和有技艺的劳动力,公司想知道每天生产多少数量的碗和杯子可以最大化利润?
产品 |
资源需求 |
||
劳动力 (小时/单位) |
黏土 (磅/单位) |
利润 (美元/单位) |
|
碗 |
1 |
4 |
40 |
杯子 |
2 |
3 |
50 |
资源限制 |
40小时 |
120磅 |
|
2. 线性规划模型
3. 模型的运行结果及灵敏度报告
运行结果报告
灵敏度报告
三、 报告分析
1. 由运行结果报告得到最优解为(24,8),即碗生产24个、杯子生产8个可使利润达到最高的1360美元。
2. 当目标式系数中碗的利润在范围(即[40-15,40+26.67])内变化时,最优解(24,8)不会改变。
同理,当目标式中杯子的利润在范围[30,80](即[50-20,50+30])内变化时,最优解(24,8)不会改变。
注:上述结论的前提是只有其中一个系数变动时才有效,如果多个同时变动时要满足百分之百法则。
3. 由灵敏度报告知,当线性规划模型达到最优解(24,8)时,资源(劳动力和黏土)的使用量分别为(40,120)。当劳动力在范围 [30,80](即[40-10,40+40])变化时,最优解不会改变,而且劳动力资源在此范围内每变化一个单位,最优值z会变化16个单位(即劳动力的影子价格);当黏土在范围[60,160](即[120-60,120+40])变化时,最优解不会改变,而且黏土资源在此范围内每变化一个单位,最优值z会变化6个单位(即黏土的影子价格)。
四、 目标式系数同时变化的百分之百法则
1. 概念
如果目标函数的系数同时变动,计算出每一系数变动量占该系数允许变动量的百分比(允许增加、允许减少分别对待);
将各个系数的变动百分比相加,如果所得的和不超过百分之一百,最优解不会改变;如果超出百分之一百,则不能确定最优解是否改变。
2. 举例
当碗和杯子的单位利润的估计值由(40,50)改为(50,45)时,则碗的单位利润增加量占其允许增量的百分比为(50-40)/26.7=37%;杯子的单位利润减少量占其允许减量的百分比(50-45)/20=25%。
二者之和为37%+25%=62%,因此最优解不变。