【机器学习入门】决策树的原理
什么是决策树?
决策树(Decision Tree) 是一种数据结构,可以用来分类和回归,决策树是数据结构,但构建决策树有一系列的算法,决策树的核心之一就是利用算法构建最佳的决策树,以达到在训练数据和测试数据都表现优秀的效果。
决策树的构建和人类的思维过程非常的类似。
假设,我现在要招聘算法工程师,现在有下面一份已经存在的面试记录。
| 姓名 | PYTHON | 机器学习 | 数学 | 录取 |
|---|---|---|---|---|
| 莫大 | 会 | 会 | 低 | 是 |
| 柯二 | 不会 | 会 | 高 | 是 |
| 张三 | 不会 | 会 | 低 | 否 |
| 李四 | 不会 | 不会 | 高 | 否 |
| 王五 | 会 | 不会 | 低 | 否 |
| 赵六 | 不会 | 不会 | 高 | 否 |
| 秦七 | 会 | 不会 | 高 | 否 |
| 古八 | 会 | 不会 | 低 | 否 |
| 宋九 | 不会 | 不会 | 低 | 否 |
那好,现在有一个新的求职者的面试记录
| 姓名 | PYTHON | 机器学习 | 数学 | 录取 |
|---|---|---|---|---|
| 朱十 | 不会 | 会 | 低 | ? |
现在的问题是,该不该录取宋九?
决策树就是用来解决这类问题的。
比如,我们可以这样思考。
这是流程图,我们大概都是这样思考问题的。
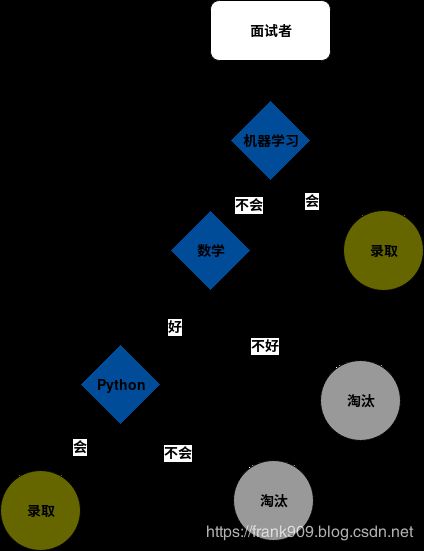
翻译成决策树如下图所示:
这里需要注意两个重要的概念。
内部节点
上图中菱形表示的都是内部节点,内部节点用来表示特征或者属性。
机器学习、数学、Python 这些都是数据集中的特征。
叶节点
叶节点表示类别。
上图位于每个分支末端的圆形都是叶节点。
我们本次示例中的类别有两种,录取和淘汰。
当我们顺着决策树进行决策时,很自然地会有一个答案。
心细的同学会有疑问,既然有多种特征,为什么上面的决策树一定要把机器学习作为根节点呢?
是的,把不同的特征作为根节点构建决策树都可以,但是最后的效果就不一样。
上面可以看到,决策树是构建成功了,但是效果恐怕不能让人满意。
所以,决策树最核心的一步就是选择合适的根节点,然后递归进行。
怎么做呢?
这里通过数学手段完成。
决策树中的数学
决策树中用到的数学知识可以看做是条件概率和熵的结合,实际上构建一棵决策树可以看做是拟合一种条件概率分布。
我们先简单回顾一下条件概率。
条件概率
事件 A:明天会下雨的
事件 B: 明天去加班
条件概率 P(B|A) 就是明天下雨的情况下,同时会要求加班的概率。
如果 A 和 B 是独立事件,那么条件概率就是 P(A)*P(B)
再回到我们的示例,我们可以这样看
事件 A:面试者会 Python
事件 B:面试者被录取
那么条件概率就是 P(B|A) 面试者会 Python 同时被录取的概率。
从根节点到叶节点,每一条路径对应一个条件概率,所以条件概率可以共同组成一个概率分布。
前面讲到过,选择哪一个特征作为决策树的根节点是非常重要的,这里需要另外一个数学知识解决,那就是熵(entropy)。
熵
熵本来是物理概念,用来衡量一个封闭的系统中无法利用的能量。
在信息论中,熵是用来度量系统的不确定程度的。
怎么理解呢?
我们通常说一个人靠谱或者是不靠谱,这个通常是比较感性的,做感性的判断容易终究不好,所以很多人想到了量化。
比方说,判断某个人能不能完成任务的概率为 P.
- P = 0,说明这个人的能力很差,肯定不能完成任务
- P = 1, 说明这个人的能力很强,绝对可以完成任务
我们用熵来定义不确定性。
熵的公式如下
H ( X ) = − ∑ i = 1 n p i log p i H(X)=-\sum_{i=1}^{n}p_{i}\log p_{i} H(X)=−i=1∑npilogpi
如果 P 只有 0 或者 1 两种取值的话。
熵的结果都是 0.
熵等于 0 的意思是,百分百肯定,没有什么不确定的。
下次你再听到别人说:“我早就知道你肯定不行”
这个时候,你要在心里翻译过来,他对你建立了一个判断模型,这个模型中他认为熵几乎为 0,没有什么不确定性,他看死你了。
下面再讲条件熵。
对比之前的条件概率,我们可以很容易理解。
条件熵H(Y|X)是衡量在随机变量X已经确定的条件下,Y取值的不确定性。
可以这么理解。
假设随机变量 X 表示面试者的 Python 等级,取值有会和不会两种。
随机变量 Y 表示最终的录取结果,有录取和淘汰两种。
那么,H(Y|X) 就是已知面试者的 Python 等级,求面试者最终录取结果的不确定性。
公式如下:
H ( Y ∣ X ) = ∑ i = 1 n p i H ( Y ∣ X = x i ) H(Y|X) = \sum_{i=1}^{n}p_{i}H(Y|X=x_{i}) H(Y∣X)=i=1∑npiH(Y∣X=xi)
信息增益(information gain)
有了熵和条件熵还不够,我们的目的是减少熵,为此引入了信息增益。
g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A) = H(D) - H(D|A) g(D,A)=H(D)−H(D∣A)
上面 D 指代训练集。
H(D) 被称为经验熵。
H(D|A) 经验条件熵
g(D,A) A 对 D 的信息增益
H(D) 说明的是训练集合,分类的不确定程度。
H(D|A) 说明的是特征 A 选定条件下,训练集的分类不确定程度。
g(D,A) 说明的是选定特征 A 后,对于提升 D 的分类确定性有多少。
g(D,A) 自然是越高越好,这也是它增益的意义体现。
不同的特征,信息增益不一样,所以它们对于构建准确的决策树价值也不一样。
我们构建决策树时,以信息增益最大的特征为基础。
信息增益
我们可以针对示例中不同的特征,求其信息增益
首先看经验熵。
所以的训练样本记为 D,分类结果为 C
C 有两种取值:录取和淘汰
| 姓名 | PYTHON | 机器学习 | 数学 | 录取 |
|---|---|---|---|---|
| 莫大 | 会 | 会 | 低 | 是 |
| 柯二 | 不会 | 会 | 高 | 是 |
| 张三 | 不会 | 会 | 低 | 否 |
| 李四 | 不会 | 不会 | 高 | 否 |
| 王五 | 会 | 不会 | 低 | 否 |
| 赵六 | 不会 | 不会 | 高 | 否 |
| 秦七 | 会 | 不会 | 高 | 否 |
| 古八 | 会 | 不会 | 低 | 否 |
| 宋九 | 不会 | 不会 | 低 | 否 |
我们观察表格,可以知道录取 2 人,淘汰 7 人,共 9 人。
H ( D ) = − ∑ k = 1 K ∣ C k ∣ ∣ D ∣ log 2 ∣ C k ∣ ∣ D ∣ H(D) = -\sum_{k=1}^{K}\frac{|C_{k}|}{|D|}\log_{2}\frac{|C_{k}|}{|D|} H(D)=−k=1∑K∣D∣∣Ck∣log2∣D∣∣Ck∣
C k C_{k} Ck 表示某一类别, ∣ C k ∣ |C_{k}| ∣Ck∣ 该类别下的样本数量。
比如 C 1 C_{1} C1代表录取的人,录取的人数是 2 个, C 2 C_{2} C2代表淘汰的人,淘汰的人数是 7 个。
所以
H ( D ) = − 2 9 ∗ log 2 2 9 − 7 9 ∗ log 2 7 9 = 0.764 H(D)=-\frac{2}{9}*\log_{2} \frac{2}{9}-\frac{7}{9}*\log_{2} \frac{7}{9} = 0.764 H(D)=−92∗log292−97∗log297=0.764
经验条件熵也有公式
H ( D , A ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ H ( D i ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ ∑ k = 1 K log 2 ∣ D i k ∣ ∣ D i ∣ H(D,A) = -\sum_{i=1}^{n}\frac{|D_{i}|}{|D|}H(D_{i})=-\sum_{i=1}^{n}\frac{|D_{i}|}{|D|}\sum_{k=1}^{K}\log_{2}\frac{|D_{ik}|}{|D_{i}|} H(D,A)=−i=1∑n∣D∣∣Di∣H(Di)=−i=1∑n∣D∣∣Di∣k=1∑Klog2∣Di∣∣Dik∣
公式可能比较复杂,但是还是比较容易理解的。
A 指代某种特征,A 将 D D D 划分了不同的子集, D i D_{i} Di 是某一个子集。 ∣ D i ∣ |D_{i}| ∣Di∣ 是对应的子集中样本的数量。
比如按照Python 这个特征,可以将 D 划分为 D1,D2 两个子集,D1 代表会,D2 代表不会。两者的数量分别为 4 和 5。
D i k D_{ik} Dik 表示 Di 子集中,属于类别 C k C_{k} Ck 的集合。
比如会 Python 的人中,最终被录取的那些人。
下面求Python这一特征的经验条件熵,设 Python 为 特征 A1.
H ( D 1 ) = − 1 4 ∗ log 2 1 4 − 3 4 ∗ log 2 3 4 = 0.811 H(D_{1})=-\frac{1}{4}*\log_{2} \frac{1}{4}-\frac{3}{4}*\log_{2} \frac{3}{4} = 0.811 H(D1)=−41∗log241−43∗log243=0.811
H ( D 2 ) = − 1 5 ∗ log 2 1 5 − 4 5 ∗ log 2 4 5 = 0.722 H(D_{2})=-\frac{1}{5}*\log_{2} \frac{1}{5}-\frac{4}{5}*\log_{2} \frac{4}{5} = 0.722 H(D2)=−51∗log251−54∗log254=0.722
H ( D , A 1 ) = − 2 9 ∗ H ( D 1 ) − 7 9 ∗ H ( D 2 ) = 0.762 H(D,A_{1})=-\frac{2}{9}*H(D_{1})-\frac{7}{9}*H({D_{2}}) = 0.762 H(D,A1)=−92∗H(D1)−97∗H(D2)=0.762
有了 H ( D ) H(D) H(D)和 H ( D , A ) H(D,A) H(D,A)之后,就可以求信息增益了
g ( D , A 1 ) = H ( D ) − H ( D , A 1 ) = 0.764 − 0.762 = 0.002 g(D,A_{1})=H(D)-H(D,A_{1}) = 0.764 - 0.762 = 0.002 g(D,A1)=H(D)−H(D,A1)=0.764−0.762=0.002
增益为 0.002 ,这代表着以 Python 为特征划分数据集 D,对于减少分类不确定性毫无帮助。
那么,设机器学习为 A2,数学为 A3,按照同样的结果,它们的信息增益分别是:
H ( D , A 2 ) = − 3 9 ∗ 0.918 − 6 9 ∗ 0 = 0.306 g ( D , A 2 ) = 0.764 − 0.306 = 0.458 H(D,A_{2}) = -\frac{3}{9}*0.918- \frac{6}{9}*0 = 0.306 g(D,A_{2}) = 0.764 - 0.306 = 0.458 H(D,A2)=−93∗0.918−96∗0=0.306g(D,A2)=0.764−0.306=0.458
H ( D , A 3 ) = − 4 9 ∗ 0.811 − 5 9 ∗ 0.722 = 0.762 g ( D , A 2 ) = 0.764 − 0.762 = 0.002 H(D,A_{3}) = -\frac{4}{9}*0.811 -\frac{5}{9}*0.722= 0.762 g(D,A_{2}) = 0.764 - 0.762 = 0.002 H(D,A3)=−94∗0.811−95∗0.722=0.762g(D,A2)=0.764−0.762=0.002
按照信息增益,机器学习应该就是最关键的特征。
但是,信息增益 有个缺点,就是结果容易偏向样本多的特征。
因此,除了信息增益外还有个信息增益比.
定义如下
g R ( D , A ) = g ( D , A ) H A ( D ) g_{R}(D,A)=\frac{g(D,A)}{H_{A}(D)} gR(D,A)=HA(D)g(D,A)
其中,
H A ( D ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ log 2 ∣ D i ∣ ∣ D ∣ H_A(D)=-\sum_{i=1}^{n}\frac{|D_{i}|}{|D|}\log_{2}\frac{|D_{i}|}{|D|} HA(D)=−i=1∑n∣D∣∣Di∣log2∣D∣∣Di∣
我们也可以按照公式来计算,每个特征的信息增益比。
g R ( D , A 1 ) = 0.003 g_{R}(D,A_{1}) = 0.003 gR(D,A1)=0.003
g R ( D , A 2 ) = 0.499 g_{R}(D,A_{2}) = 0.499 gR(D,A2)=0.499
g R ( D , A 3 ) = 0.003 g_{R}(D,A_{3}) = 0.003 gR(D,A3)=0.003
可以看到,仍然说明了机器学习是录取判断中的关键特征。
特征的选取是递归进行的,先选取最优的特征,然后用同样的方法选取次优的特征,直到满足预设的条件。
常见的有 2 种算法,ID3 和 C4.5。
ID3 是以信息增益为选择依据,C4.5 以信息增益比为算法依据。
后续的博文将详细讲解它们的算法实践过程。