【笔记】单源点最短路径

1.单源点最短路径

  单源点最短路径问题：给定图G=(V,E)，每条边(i,j)上都标有非负实数C[i][j]作为它的权；在图中指定一个顶点v作为源点，求从v到其他每个顶点的最短路径长度。单源最短路问题的进一步推广是求每对顶点之间的最短路径。

---

2.迪杰斯特拉算法

  基本思想：将V分成两个集合S和V-S。其中S是最短路径已经确定的顶点集合；V-S是最短路径尚未确定的顶点集合。每一步从V-S中选一个顶点w加入S，使S中从源点到其余顶点的路长最短，此过程进行到V-S变为空为止。

  设有一个带权有向图D=(V,E)，定义一个数组dist，数组中的每个元素dist[i]表示顶点 v0 到顶点 vi 存在弧，则dist[i]是弧 <v0,vj> 的权值；否则dist[j]为 ∞ 。显然，长度为 dist[j]=Min{dist[i]|vi∈V} 的路径表示从顶点 v0 到顶点 vi 的最短路径，此路径为 <v0,vj> 。即，在所有的顶点 v0 到顶点 vi 的路径中，dist[j]是最短的一条路径。
  假设次短的路径的终点为 vk ，则这条路径或者是 <v0,vk> 或者是 <v0,vj,vk> ，它的长度或者是 v0 到 vk 的弧上的权值，或者是dist[j]和从 vj 到 vk 的弧上的权值之和。
  一般情况下，下一条长度次短的路径的长度一定是 dist[j]=Min{dist[i]|vi∈V−S} ，dist[i]或者是弧 <v0,vi> 上的权值，或者是 dist[k](vk∈V−S) 与弧 <vk,vj> 的权值之和。

  算法步骤：
  1. 假设用带权的邻接矩阵arc表示带权的有向图，arc[i][j]表示弧 <vi,vj> 上的权值，若 <vi,vj> 不存在，则置arc[i][j]为 ∞ 。S为已找到从v出发的最短路径的终点的集合。初始时，S只包括源点 v0 ，即 S=v0 ，V-S包括出 v0 以外的其他顶点。 v0 到其他顶点的路径初始化为dist[i]=G.arc[0][i].adj。
  2. 选择距离顶点 vi 最短的顶点 vj ，使得 dist[j]=Min{dist[j]|vi∈V−S} 。dist[j]表示从 v0 到 vj 的最短路径长度， vj 表示对应的终点。
  3. 修改从 v0 到顶点 vi 的最短路径长度，其中 vi∈S 。如果有 dist[k]+G.arc[k][i].adj<dist[i] ，则修改dist[i]，使得 dist[i]=dist[k]+G.arc[k][i].adj 。
  4. 重复执行2和3共n-1次，可求出所有从 v0 到其他顶点的最短路径长度。

  时间复杂性：设有向图G有n个顶点和e条边，当采用邻接矩阵表示有向图时，时间复杂度为 O(n2) ；如果e远小于 n2 ，采用邻接表表示有向图时效率更高，时间复杂度为 O(e) 。

---

3.迪杰斯特拉算法实现

typedef int PathMatrix[MaxSize][MaxSize];   /*定义一个保存最短路径的二维数组*/
typedef int ShortPathLength[MaxSize];       /*定义一个保存从顶点v0到顶点v的最短距离的数组*/
void Dijkstra (MGraph N,int v0, PathMatrix path,ShortPathLength dist)
/*用Dijkstra算法求有向网N的v0顶点到其余各顶点v的最短路径path[v]和最短路径长度dist[v]*/
/*final[v]为1表示v∈S，即已经求出从v0到v的最短路径*/
{ 
    int v,w,i,k,min;
    int final[MaxSize];         /*记录v0到该顶点的最短路径是否已求出*/
    for(v=0;v/*数组dist存储v0到v的最短距离，初始化为v0到v的弧的距离*/
    {
        final[v]=0;
        dist[v]=N.arc[v0][v].adj;
        for(w=0;w0;
        if(dist[v]/*如果从v0到v有直接路径，则初始化路径数组*/
        {
            path[v][v0]=1;
            path[v][v]=1;
        }
    }
    dist[v0]=0;                     /*v0到v0的路径为0*/
    final[v0]=1;                    /*v0顶点并入集合S*/
    /*从v0到其余G.vexnum-1个顶点的最短路径，并将该顶点并入集合S*/
    for(i=1;ifor(w=0;wif(!final[w]&&dist[w]/*在不属于集合S的顶点中找到离v0最近的顶点*/
            {
                v=w;                /*将其离v0最近的顶点w赋给v，其距离赋给min*/
                min=dist[w];
            }
        final[v]=1;             /*将v并入集合S*/
        for(w=0;w/*利用新并入集合S的顶点，更新v0到不属于集合S的顶点的最短路径长度和最短路径数组*/
            if(!final[w]&&minfor(k=0;k1;
            }
    }
}

  其中二维数组path[v][w]如果为1，则表示从顶点 v0 到顶点v 的最短路径经过顶点w；以为数组dist[v]表示从顶点 v0 到顶点v的当前求出的最短路径长度。先利用 v0 到其他顶点的弧的对应的权值将数组path和dist初始化，然后找出从 v0 到顶点v（不属于集合S）的最短路径，并将v并入集合S，最短路径长度赋给min。接着利用新并入的顶点v，更新 v0 到其他顶点（不属于集合S）的最短路径长度和最短路径数组。重复以上步骤，直到从 v0 到所有其他顶点的最短路径都求出为止。

---

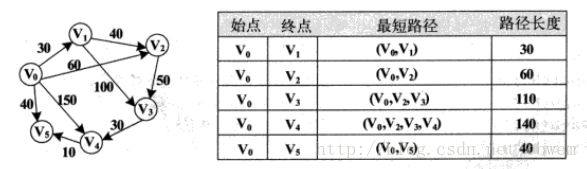
4.应用实例

  创建一个如上图所示的有向网N，输出该有向网N从 v0 开始到其他各顶点的最短路径及最短路径长度。

• 类型定义

#include
#include
#include
#include
typedef char VertexType[4];
typedef char InfoPtr;
typedef int VRType;
#define INFINITY 100000         /*定义一个无限大的值*/
#define MaxSize 50              /*最大顶点个数*/
typedef int PathMatrix[MaxSize][MaxSize];   /*定义一个保存最短路径的二维数组*/
typedef int ShortPathLength[MaxSize];       /*定义一个保存从顶点v0到顶点v的最短距离的数组*/
typedef enum{DG,DN,UG,UN}GraphKind;     /*图的类型：有向图、有向网、无向图和无向网*/
typedef struct
{
    VRType adj;             /*对于无权图，用1表示相邻，0表示不相邻；对于带权图，存储权值*/
    InfoPtr *info;              /*与弧或边的相关信息*/
}ArcNode,AdjMatrix[MaxSize][MaxSize];
typedef struct                  /*图的类型定义*/
{
    VertexType vex[MaxSize];    /*用于存储顶点*/
    AdjMatrix arc;              /*邻接矩阵，存储边或弧的信息*/
    int vexnum,arcnum;          /*顶点数和边（弧）的数目*/
    GraphKind kind;             /*图的类型*/
}MGraph;
typedef struct                  /*添加一个存储网的行、列和权值的类型定义*/
{
    int row;
    int col;
    int weight;
}GNode;

• Dijkstra算法

void Dijkstra(MGraph N,int v0,PathMatrix path,ShortPathLength dist)
/*用Dijkstra算法求有向网N的v0顶点到其余各顶点v的最短路径P[v]及带权长度D[v]*/
/*final[v]为1表示v∈S，即已经求出从v0到v的最短路径*/
{
    int v,w,i,k,min;
    int final[MaxSize];         /*记录v0到该顶点的最短路径是否已求出*/
    for(v=0;v/*数组dist存储v0到v的最短距离，初始化为v0到v的弧的距离*/
    {
        final[v]=0;
        dist[v]=N.arc[v0][v].adj;
        for(w=0;w0;
        if(dist[v]/*如果从v0到v有直接路径，则初始化路径数组*/
        {
            path[v][v0]=1;
            path[v][v]=1;
        }
    }
    dist[v0]=0;                     /*v0到v0的路径为0*/
    final[v0]=1;                    /*v0顶点并入集合S*/
    /*从v0到其余G.vexnum-1个顶点的最短路径，并将该顶点并入集合S*/
    for(i=1;imin=INFINITY;
        for(w=0;wif(!final[w]&&dist[w]<min)  /*在不属于集合S的顶点中找到离v0最近的顶点*/
            {
                v=w;                    /*将其离v0最近的顶点w赋给v，其距离赋给min*/
                min=dist[w];
            }
            final[v]=1;                 /*将v并入集合S*/
            for(w=0;w/*利用新并入集合S的顶点，更新v0到不属于集合S的顶点的最短路径长度和最短路径数组*/
                if(!final[w]&&minmin+N.arc[v][w].adjmin+N.arc[v][w].adj;
                    for(k=0;k1;
                }
    }
}

• 邻接矩阵创建有向网

void CreateGraph(MGraph *N,GNode *value,int vnum,int arcnum,VertexType *ch)
/*采用邻接矩阵表示法创建有向网N*/
{
    int i,j,k,w,InfoFlag,len;
    char s[MaxSize];
    VertexType v1,v2;
    N->vexnum=vnum;
    N->arcnum=arcnum;
    for(i=0;ivex[i],ch[i]);

    for(i=0;ivexnum;i++)        /*初始化邻接矩阵*/
        for(j=0;jvexnum;j++)
        {
            N->arc[i][j].adj=INFINITY;
            N->arc[i][j].info=NULL; /*弧的信息初始化为空*/
        }
    for(k=0;kvalue[k].row;
        j=value[k].col;
        N->arc[i][j].adj=value[k].weight;
    }

    N->kind=DN;                     /*图的类型为有向网*/
}

• 输出图

void DisplayGraph(MGraph N)
/*输出邻接矩阵存储表示的图N*/
{
    int i,j;
    printf("有向网具有%d个顶点%d条弧，顶点依次是: ",N.vexnum,N.arcnum);
    for(i=0;i*输出网的顶点*/
        printf("%s ",N.vex[i]);
    printf("\n有向网N的:\n");           /*输出网N的弧*/
    printf("序号i=");
    for(i=0;iprintf("%8d",i);
    printf("\n");
    for(i=0;iprintf("%8d",i);
        for(j=0;jprintf("%8d",N.arc[i][j].adj);
        printf("\n");
    }
}

• 主程序

void main()
 {
   int i,j,vnum=6,arcnum=9;
   MGraph N;
   GNode value[]={{0,1,30},{0,2,60},{0,4,150},{0,5,40},
                    {1,2,40},{1,3,100},{2,3,50},{3,4,30},{4,5,10}};
   VertexType ch[]={"v0","v1","v2","v3","v4","v5"};
   PathMatrix path;                     /*用二维数组存放最短路径所经过的顶点*/
   ShortPathLength disc;                /*用一维数组存放最短路径长度*/
   CreateGraph(&N,value,vnum,arcnum,ch); /*创建有向网N*/
   DisplayGraph(N);                     /*输出有向网N*/
   Dijkstra(N,0,path,disc);
   printf("%s到各顶点的最短路径长度为：\n",N.vex[0]);
   for(i=0;i<N.vexnum;++i)
     if(i!=0)
       printf("%s-%s:%d\n",N.vex[0],N.vex[i],disc[i]);
 }

• 测试结果