吴恩达神经网络与深度学习——深度神经网络
- 深度神经网络
- 前向传播
- 矩阵维度
- 为什么使用深层表示
- 搭建深层神经网络块
- 前向和反向传播
- 参数和超参数
- 和大脑的关系
深度神经网络

符号

l:层数
l = 4
n^[l]:每一次的单元数
n^[1] = 5 n^[2] = 5 n^[3] = 3 n^[4] = 1
a^[l]:每一次的激活函数
a^[l] = g^[l](z^[l])
w^[l]:每一次的权值
b^[l]:每一次的偏置
前向传播
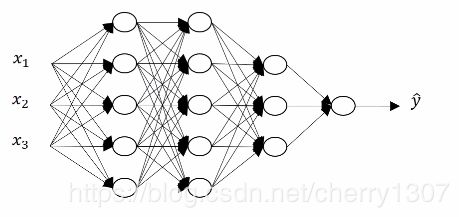
x
z^[1] = w^[1]x + b^[1]
a^[1] = g^[1](z^[1])
z^[2] = w^[2]a^[1] + b^[2]
a^[2] = g^[2](z^[2])
z^[3] = w^[3]a^[2] + b^[3]
a^[3] = g^[3](z^[3])
z^[4] = w^[4]a^[3] + b^[4]
a^[4] = g^[4](z^[4])
for l =1 to 4
z^[l] = w^[l]a^[l-1] + b^[l]
a^[l] = g^[l](z^[l])
#m个样本向量化
Z^[1] = W^[1]A^[0] + b^[1] # X=A^[0]
A^[1] = g^[1](Z^[1])
Z^[2] = W^[2]A^[1]+ b^[2]
A^[2] = g^[2](z^[2])
Z^[3] = W^[3]A^[2] + b^[3]
A^[3] = g^[3](Z^[3])
Z^[4] = W^[4]A^[3] + b^[4]
A^[4] = g^[4](Z^[4])
for l = 1 to 4
Z^[l] = w^[l]A^[l-1] + b^[l]
A^[l] = g^[l](Z^[l])
矩阵维度
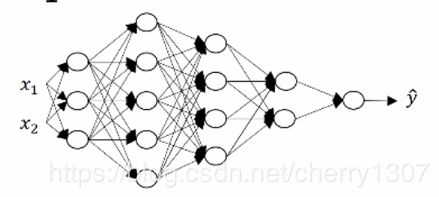
n^[0] = 2
n^[1] = 3
n^[2] = 5
n^[3] = 4
n^[4] = 2
n^[4] = 1
z^[1] = w^[1] x + b^[1]
(3,1) (3,2) (2,1) (3,1)
(n^[1],1) (n^[1],n^[0]) (n^[0],1) (n^[1],1)
a^[1] = g^[1](z^[1])
(3,1) (3,1)
(n^[1],1) (n^[1],1)
z^[2] = w^[2] a^[1] + b^[1]
(5,1) (5,3) (3,1) (5,1)
(n^[2],1) (n^[2],n^[1]) (n^[1],1) (n^[2],1)
a^[2] = g^[2](z^[2])
(5,1) (5,1)
(n^[2],1) (n^[2],1)
z^[3] = w^[3] a^[2] + b^[3]
(4,1) (4,5) (5,1) (4,1)
(n^[3],1) (n^[3],n^[2]) (n^[2],1) (n^[3],1)
a^[3] = g^[3](z^[3])
(4,1) (4,1)
(n^[3],1) (n^[3],1)
z^[4] = w^[4] a^[3] + b^[4]
(2,1) (2,4) (4,1) (2,1)
(n^[4],1) (n^[4],n^[3]) (n^[3],1) (n^[4],1)
a^[4] = g^[4](z^[4])
(2,1) (2,1)
(n^[4],1) (n^[4],1)
z^[5] = w^[5] a^[4] + b^[5]
(1,1) (1,2) (2,1) (1,1)
(n^[5],1) (n^[5],n^[4]) (n^[4],1) (n^[5],1)
a^[5] = g^[5](z^[5])
(1,1) (1,1)
(n^[5],1) (n^[5],1)
for l = 1 to 5
z^[l] = w^[l] a^[l-1] + b^[l]
(n^[l],1) (n^[l],n^[l-1]) (n^[l-1],1) (n^[l],1)
a^[l] = g^[l](z^[l])
(n^[l],1) (n^[l],1)
m个样本
Z^[1] = W^[1] X + b^[1]
(3,m) (3,2) (2,m) (3,1)
(n^[1],m) (n^[1],n^[0]) (n^[0],m) (n^[1],1)
A^[1] = g^[1](Z^[1])
(3,m) (3,m)
(n^[1],m) (n^[1],m)
Z^[2] = W^[2] A^[1] + b^[1]
(5,m) (5,3) (3,m) (5,1)
(n^[2],m) (n^[2],n^[1]) (n^[1],m) (n^[2],1)
A^[2] = g^[2](Z^[2])
(5,m) (5,m)
(n^[2],m) (n^[2],m)
Z^[3] = W^[3] A^[2] + b^[3]
(4,m) (4,5) (5,m) (4,1)
(n^[3],m) (n^[3],n^[2]) (n^[2],m) (n^[3],1)
A^[3] = g^[3](Z^[3])
(4,m) (4,m)
(n^[3],m) (n^[3],m)
Z^[4] = W^[4] A^[3] + b^[4]
(2,m) (2,4) (4,m) (2,1)
(n^[4],m) (n^[4],n^[3]) (n^[3],m) (n^[4],1)
A^[4] = g^[4](Z^[4])
(2,m) (2,m)
(n^[4],m) (n^[4],m)
Z^[5] = W^[5] A^[4] + b^[5]
(1,m) (1,2) (2,m) (1,1)
(n^[5],m) (n^[5],n^[4]) (n^[4],m) (n^[5],1)
A^[5] = g^[5](Z^[5])
(1,m) (1,m)
(n^[5],m) (n^[5],m)
for l = 1 to 4
Z^[l] = w^[l] A^[l-1] + b^[l]
(n^[l],m) (n^[l],n^[l-1]) (n^[l-1],m) (n^[l],1)
A^[l] = g^[l](Z^[l])
(n^[l],m) (n^[l],m)
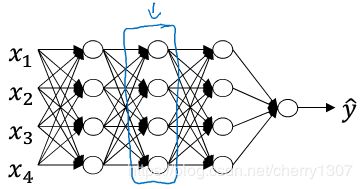
为什么使用深层表示
深度神经网络有很多的隐层,较早的前几层能学习一些低层次的简单特征,后几层就能将简单的特征结合起来去探测更加复杂的东西
搭建深层神经网络块
第l层参数: w^[l],b^[l]
前向传播: 输入 a^[l-1] 输出 a^[l] 存储 z^[l]
z^[l] = w^[l]a^[l-1] + b^[l]
a^[l] = g^[l](z^[l])
反向传播: 输入 da^[l] 输出da^[l-1] dw^[l] db^[l]
前向传播存储的z^[l]
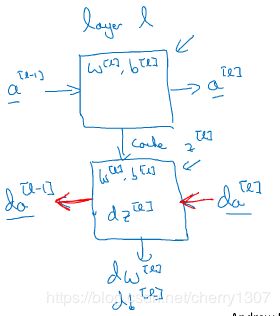
正向传播和反向传播
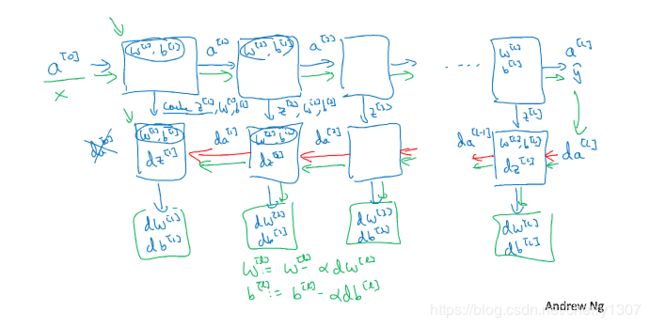
从a^[0]开始,也就是x,经过一系列正向传播计算得到yhat,之后再用输出值计算实现反向传播,得到所有的导数项,w,b也在每一层更新
编程细节:将z^[l],w^[l],b^[l]存储
前向和反向传播
前向传播
前向传播: 输入 a^[l-1] 输出 a^[l] 存储 z^[l]
z^[l] = w^[l]a^[l-1] + b^[l]
a^[l] = g^[l](z^[l])
向量化:
Z^[l] = W^[l]A^[l-1] + b^[l]
A^[l] = g^[l](Z^[l])
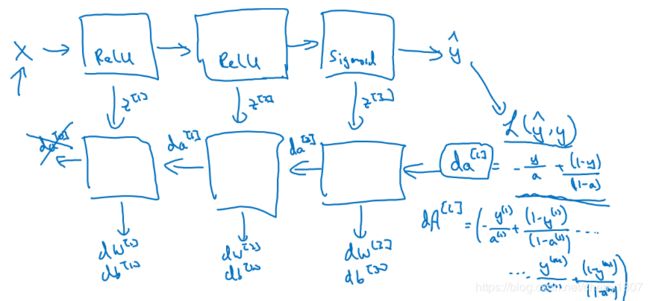
反向传播
反向传播: 输入 da^[l] 输出da^[l-1] dw^[l] db^[l]
dz^[l] = da^[l]*g'^[l](z^[l])
dw^[l] = dz^[l]a^[l-1]
db^[l] = dz^[l]
da^[l-1] = w^[l]Tdz^[l]
dz^[l] = w^[l+1]Tdz^[l+1]*g'^[l](z^[l])
向量化:
dZ^[l] = dA^[l]*g'^[l](Z^[l])
dW^[l] =(1/m)dZ^[l]A^[l-1]T
db^[l] = (1/m)np.sum(dZ^[l],axis = 1,keepdims = True)
dA^[l-1] = W^[l]TdZ^[l]
dZ^[l] = W^[l+1]TdZ^[l+1]*g'^[l](Z^[l])
参数和超参数
参数: w^[1],b^[1],w^[2],b^[2]...
超参数:
学习率:alpha
循环下降法的迭代次数:iteration
隐藏层数:l
隐藏单元数:n^[1],n^[2]...
激活函数:sigmoid ,relu, tanh
和大脑的关系









