吴恩达深度学习课程笔记(一):神经网络与深度学习
吴恩达深度学习课程笔记(一):神经网络与深度学习
- 吴恩达深度学习课程笔记(一):神经网络与深度学习
- 第一周:深度学习概论
- 第二周 神经网络基础
- 2.1 二分类
- 2.2 逻辑回归
- 2.3 逻辑回归的代价函数
- 2.4 梯度下降
- 2.5 导数
- 2.6 更多关于导数的例子
- 2.7 计算图
- 2.8计算图上的导数
- 2.9逻辑回归的梯度下降
- 2.10 在整个样本集上的梯度下降
- 2.11 矢量化
- 2.12更多矢量化的例子
- 2.13 矢量化量化逻辑回归(正向)
- 2.14 矢量化逻辑回归的梯度下降(反向)
- 2.15 Python 的numpy的广播机制
- 2.16 广播的注意事项—技巧
- 2.17 Jupyter or iPython的快速指南
- 2.18 逻辑回归代价函数的扩展
- 第三周 浅层神经网络
- 3.1 神经网络概述
- 3.2 神经网络表示
- 3.3 计算神经网络的输出
- 3.4 多个例子中的向量化
- 3.5 向量化的解释
- 3.6 激活函数
- 3.7 为什么需要非线性激活函数
- 3.8 激活函数的导数
- 3.9 神经网络的梯度下降法
- 3.10 直观理解反向传播
- 3.11 随机初始化
- 第四周 深层神经网络
- 4.1 深层神经网络
- 4.2 深层神经网络的前向传播
- 4.3 核对 矩阵的维数
- 4.4 为什么使用深层表示
- 4.5 搭建深层神经网络块
- 4.6 前向传播和反向传播
- 4.7 参数 vs 超参数
- 4.8 这和大脑有什么关系
第一周:深度学习概论
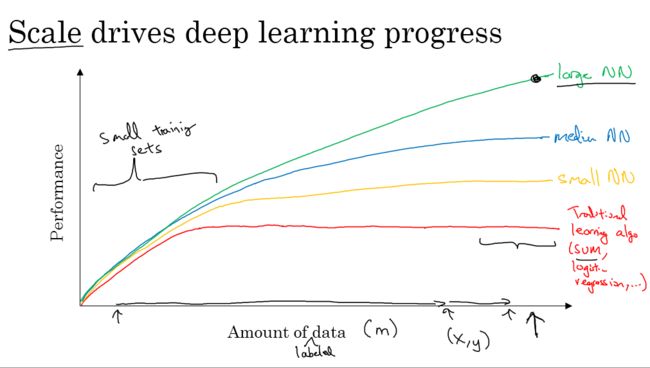
数据量大的时候大的网络能提高性能。在小的数据集上,我们更应该关注特征的选取、算法实现的细节之类的内容,因为在小的数据集上,各种规模的网络表现差不多。
第二周 神经网络基础
2.1 二分类

使用这种方式表达样本在神经网络中是更常见的方式,即,每一列表示一个样本,每一行表示一个特征。
m 样本数量
n 特征数量
2.2 逻辑回归
- 用sigmoid函数去限制 WX+b W X + b 的范围,即为逻辑回归。
y^=σ(wx+b), where σ(z)=11+e−z y ^ = σ ( w x + b ) , w h e r e σ ( z ) = 1 1 + e − z
2.3 逻辑回归的代价函数
L(y,y^)=−ylog(y^)−(1−y)log(1−y^) L ( y , y ^ ) = − y l o g ( y ^ ) − ( 1 − y ) l o g ( 1 − y ^ )
Cost function:
2.4 梯度下降
repeat:{ r e p e a t : {
w=w−α∂J(w)∂w w = w − α ∂ J ( w ) ∂ w
b=b−α∂J(b)∂b b = b − α ∂ J ( b ) ∂ b
} }
2.5 导数
略
2.6 更多关于导数的例子
略
2.7 计算图
略
2.8计算图上的导数
链式法则
2.9逻辑回归的梯度下降
a表示的是 y^ y ^ ,即逻辑回归的预测值。
对于sigmoid函数的求导为:
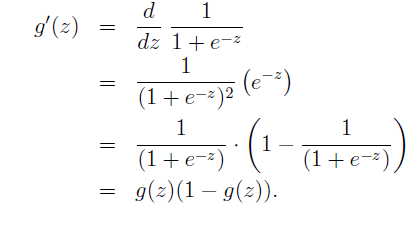
即 σ(z)′=σ(z)( 1−σ(z) ) σ ( z ) ′ = σ ( z ) ( 1 − σ ( z ) ) 。

dw1=x1dz d w 1 = x 1 d z 、 dw2=x2dz d w 2 = x 2 d z 、 db=dz d b = d z
那么,沿着代价函数梯度下降的方向更新参数:
w1=w1−α dw1 w 1 = w 1 − α d w 1
w2=w2−α dw2 w 2 = w 2 − α d w 2
b=b−α db b = b − α d b
就可以最终到达一个局部最优点。
这就是逻辑回归的梯度下降。
推导的最终结果是,我们在梯度下降的时候,不需要再去推导,直接利用结论
目前为止还只是单个样本的梯度下降。
2.10 在整个样本集上的梯度下降
Random initialization w1、w2、b R a n d o m i n i t i a l i z a t i o n w 1 、 w 2 、 b
Repeat until convergence: R e p e a t u n t i l c o n v e r g e n c e :
1. J=0, dw1=0, dw2=0, db=0 J = 0 , d w 1 = 0 , d w 2 = 0 , d b = 0
2. For i=1 to m: F o r i = 1 t o m :
3. z(i)=WTX+b z ( i ) = W T X + b
4. a(i)=σ(z(i)) a ( i ) = σ ( z ( i ) )
5. dz(i)=a(i)−y(i) d z ( i ) = a ( i ) − y ( i )
6. J +=−y(i)loga(i)−(1−y(i))log(1−a(i)) J + = − y ( i ) l o g a ( i ) − ( 1 − y ( i ) ) l o g ( 1 − a ( i ) )
7. dw1 +=x(i)1dz(i) d w 1 + = x 1 ( i ) d z ( i )
8. dw2 +=x(i)2dz(i) d w 2 + = x 2 ( i ) d z ( i )
9. db +=dz(i) d b + = d z ( i )
10. end For e n d F o r
11. J=J/m J = J / m
12. dw1=dw1/m d w 1 = d w 1 / m
13. dw2=dw2/m d w 2 = d w 2 / m
14. db=db/m d b = d b / m
15. w1=w1−α dw1 w 1 = w 1 − α d w 1
16. w2=w2−α dw2 w 2 = w 2 − α d w 2
17. b=b−α db b = b − α d b
缺点:
- 需要两个for循环,第一个遍历所有样本,第二个遍历所有特征(12-13行),导致算法很低效;
- 解决办法:矢量化表示
2.11 矢量化
vectorization
矢量化使得运算过程变得更快。
试验中,矢量化比非矢量化快400多倍。
矢量化你的代码
经验法则:无论什么时候,避免显式的使用for循环。
import numpy as np
import time
a = np.random.rand(1000000)
b = np.random.rand(1000000)
tic = time.time()
c = np.dot(a, b)
toc = time.time()
print('Vectorization version :' + str(1000* (toc - tic)) + ' ms')
# Vectorization version :1.0001659393310547 ms
tic = time.time()
for i in range(len(a)):
c = a[i] * b[i]
toc = time.time()
print('NO vectorization version :' + str(1000* (toc - tic)) + ' ms')
# NO vectorization version :424.0000247955322 ms2.12更多矢量化的例子

numpy中很多函数都是直接对矩阵中的元素进行操作。
2.10的矢量化表示:
Random initialization W、b R a n d o m i n i t i a l i z a t i o n W 、 b
Repeat until convergence: R e p e a t u n t i l c o n v e r g e n c e :
1. J=0, dW=np.zeros((n,1)), db=0 J = 0 , d W = n p . z e r o s ( ( n , 1 ) ) , d b = 0
2. For i=1 to m: F o r i = 1 t o m :
3. z(i)=WTX+b z ( i ) = W T X + b
4. a(i)=σ(z(i)) a ( i ) = σ ( z ( i ) )
5. dz(i)=a(i)−y(i) d z ( i ) = a ( i ) − y ( i )
6. J +=−y(i)loga(i)−(1−y(i))log(1−a(i)) J + = − y ( i ) l o g a ( i ) − ( 1 − y ( i ) ) l o g ( 1 − a ( i ) )
7. dW +=x(i)dz(i) d W + = x ( i ) d z ( i )
9. db +=dz(i) d b + = d z ( i )
10. end For e n d F o r
11. J=J/m J = J / m
12. dW=dW/m d W = d W / m
14. db=db/m d b = d b / m
15. W=W−α dW W = W − α d W
17. b=b−α db b = b − α d b
即,W的计算去掉了循环,使用了矩阵。
减少一层循环使得代码变快。
2.13 矢量化量化逻辑回归(正向)
不用for循环
Z=wTX+b Z = w T X + b
- 其中,w为 n×1 n × 1 , wT=[w1,w2,...,wn] w T = [ w 1 , w 2 , . . . , w n ] ;
- b为 1×m 1 × m , b=[b,b,...,b] b = [ b , b , . . . , b ] ;
- X为 n×m n × m , X=[x(1),x(2),...,x(m)] X = [ x ( 1 ) , x ( 2 ) , . . . , x ( m ) ] 。
- Z∈R1×m Z ∈ R 1 × m
A=σ(Z) A = σ ( Z )
2.14 矢量化逻辑回归的梯度下降(反向)
- dZ=A−Y d Z = A − Y
- dw=1mX(dZ)T d w = 1 m X ( d Z ) T
- db=1m∑mi=1dz(i)=1m np.sum(dZ) d b = 1 m ∑ i = 1 m d z ( i ) = 1 m n p . s u m ( d Z )
再次实现算法:
1. J=0, dw=np.zeros((n,1)), db=0 J = 0 , d w = n p . z e r o s ( ( n , 1 ) ) , d b = 0
3. Z=WTX+b Z = W T X + b
4. A=σ(Z) A = σ ( Z )
5. dZ=A−Y d Z = A − Y
6. dw=1mX(dZ)T d w = 1 m X ( d Z ) T
7. db=1m∑mi=1dz(i)=1m np.sum(dZ) d b = 1 m ∑ i = 1 m d z ( i ) = 1 m n p . s u m ( d Z )
8. W=W−α dW W = W − α d W
9. b=b−α db b = b − α d b
2.15 Python 的numpy的广播机制
matrixm×n+−×÷(1,n)−−−−−−−−−−−>(m,n) m a t r i x m × n + − × ÷ ( 1 , n ) − − − − − − − − − − − > ( m , n )
matrixm×n+−×÷(m,1)−−−−−−−−−−−>(m,n) m a t r i x m × n + − × ÷ ( m , 1 ) − − − − − − − − − − − > ( m , n )
matrixm×n+−×÷(1,1)−−−−−−−−−−−>(m,n) m a t r i x m × n + − × ÷ ( 1 , 1 ) − − − − − − − − − − − > ( m , n )
2.16 广播的注意事项—技巧
因为numpy的灵活性,常常导致出现奇怪的bug。
- 不要使用秩为1的数组,向量的秩至少为2:
a = np.random.randn(1, 5)
a = np.random.randn(5, 1) - 断言向量的形状:
assert(a.shape == (5, 1))
这些assert执行起来很快,某种意义上可以看成是代码的文档,随意使用。 - 如果代码中出现秩为1的数组,使用reshape将其转换为向量:
a = np.reshape((5,1))
通过以上三种手段,彻底杜绝代码中的秩为1的数组。
2.17 Jupyter or iPython的快速指南
如果前面代码框的文本后边的代码框有用到,一定要先运行过前边的代码框。
2.18 逻辑回归代价函数的扩展
- 为什么逻辑回归的代价函数是这个样子的?
P(y|x)=y^y(1−y^)(1−y)={y^,1−y^,if y = 1if y = 0(1)(2) (1) P ( y | x ) = y ^ y ( 1 − y ^ ) ( 1 − y ) (2) = { y ^ , if y = 1 1 − y ^ , if y = 0
也就是, y^ y ^ 是在样本x的条件下,结果为 y y 的概率。
其中, y^=σ(z) y ^ = σ ( z ) , z=wTX+b z = w T X + b 。
那么,根据上边的式子,我们可以通过求极大似然估计来估算一组合理的参数值。
极大似然估计是说,我通过利用已知的样本分布,找到最有可能导致这种分布的参数值,即导致最大概率的参数值。
log(P)=ylog(y^)+(1−y)log(1−y^) l o g ( P ) = y l o g ( y ^ ) + ( 1 − y ) l o g ( 1 − y ^ )
通过log化的式子,一样可以通过找最大似然值的方式找到参数值。
log函数是严格递增函数,把上式log化,不改变增减性,带来的好处是乘积变成加减。
而损失函数是将每一个样本的损失求和(再求平均也可)。
同时损失函数的目标是求最小的损失。加负号。
将求极大似然值和最小化cost统一起来。
即: L=−ylog(y^)−(1−y)log(1−y^) L = − y l o g ( y ^ ) − ( 1 − y ) l o g ( 1 − y ^ )
最大化训练样本出现的次数相当于最小化代价函数。
那么最后, logP(所有样本)=log∏mi=1P(y(i)|x(i))=∑−L l o g P ( 所 有 样 本 ) = l o g ∏ i = 1 m P ( y ( i ) | x ( i ) ) = ∑ − L
所以, J(w,b)=−1/m∑L(y^(i),y) J ( w , b ) = − 1 / m ∑ L ( y ^ ( i ) , y )
1/m是为了缩放。
第三周 浅层神经网络
3.1 神经网络概述
略
3.2 神经网络表示
略
3.3 计算神经网络的输出
略
3.4 多个例子中的向量化
略
3.5 向量化的解释
略
3.6 激活函数
激活函数:
- sigmoid函数
a=11+e−z a = 1 1 + e − z
很少使用。 - tanh函数
a=ez−e−zez+e−z a = e z − e − z e z + e − z
结果介于-1到1之间。
有时候数据是中心化的时候,可以使用。
和sigmoid共同的缺点是:在输入很大or很小的时候,梯度变化很小,会降低梯度下降的速度。 - ReLU
修正线性单元
a=max(0, z) a = m a x ( 0 , z )
z为正,梯度为1;
z为负,梯度为0;
z = 0, 给其假设一个导数。
不同层的激活函数可以是不同的。
二分类问题,输出为0和1的,输出层选择sigmoid;其他所有层都选择ReLU。 - leaky ReLU
a=max(0.01z, z) a = m a x ( 0.01 z , z )
0.01表示一个很小的值,也可以是其他值。
效果比ReLU好。
吴恩达老师一般用ReLU。
和ReLU的共同优点是:即使输入z很大的情况下,梯度都会远远大于0;所以,使用这两个,比使用sigmoid和tanh的学习速率要快很多(因为梯度下降为0,即梯度消失的情况减少了)。
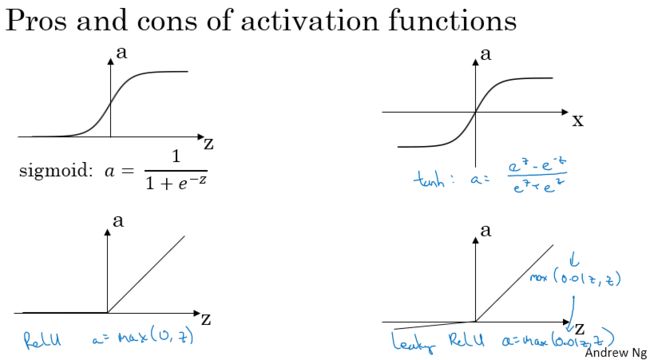
总结: - sigmoid除二分类输出层外,基本不用;
- tanh比sigmoid优秀;
- ReLU更常用;
- 如果选择 ReLU,可以尝试一下leaky ReLU,尽管最后不一定使用leaky ReLU。
- 在构建自己的网络时,如果不确定用什么激活函数,就多选择几种,测试一下。
3.7 为什么需要非线性激活函数
如果隐藏层只用线性激活函数or不用激活函数:
a[1]=z[1]=w[1]x+b[1] a [ 1 ] = z [ 1 ] = w [ 1 ] x + b [ 1 ]
a[2]=z[2]=w[2]a[1]+b[2] a [ 2 ] = z [ 2 ] = w [ 2 ] a [ 1 ] + b [ 2 ]
即:
a[2]=w[2](w[1]x+b[1])+b[2] a [ 2 ] = w [ 2 ] ( w [ 1 ] x + b [ 1 ] ) + b [ 2 ]
=(w[2]w[1])x+(w[2]b[1]+b[2]) = ( w [ 2 ] w [ 1 ] ) x + ( w [ 2 ] b [ 1 ] + b [ 2 ] )
=w′x+b′ = w ′ x + b ′
那么,仍旧是线性变换。即对输入进行线性组合然后输出。这根本就不需要什么隐藏层。
只有一个地方会用到线性激活函数or不用激活函数,就是回归问题。网络的输出是一个连续值。即 y^∈R y ^ ∈ R ,即使这样,隐藏层依然使用的是诸如tanh、ReLU or leaky ReLU,只有在输出层使用线性激活函数。
3.8 激活函数的导数
- sigmoid
g(z)=11+e−z g ( z ) = 1 1 + e − z
g′(z)=g(z)(1−g(z))=a(1−a) g ′ ( z ) = g ( z ) ( 1 − g ( z ) ) = a ( 1 − a )
- tanh
g(z)=ez−e−zez+e−z g ( z ) = e z − e − z e z + e − z
g′(z)=1−(tanh(z))2=1−a2 g ′ ( z ) = 1 − ( t a n h ( z ) ) 2 = 1 − a 2
- ReLU
g(z)=ma(0, z) g ( z ) = m a ( 0 , z )
g′(z)=⎧⎩⎨1,0,undefined,if z > 0if z < 0if z = 0 g ′ ( z ) = { 1 , if z > 0 0 , if z < 0 u n d e f i n e d , if z = 0
z=0 z = 0 处的导数在代码实现中,可以设置成1,也可以设置成0。因为碰到 z=0 z = 0 的概率不大,设置成多少对结果没多少影响。
3.9 神经网络的梯度下降法
前行传播,然后反向传播。
- Forward propagation
Z[1]=w[1]X+b[1] Z [ 1 ] = w [ 1 ] X + b [ 1 ]
A[1]=g[1](Z[1]) A [ 1 ] = g [ 1 ] ( Z [ 1 ] )
Z[2]=w[2]A[1]+b[2] Z [ 2 ] = w [ 2 ] A [ 1 ] + b [ 2 ]
A[2]=g2(Z[2])=σ(Z[2]) A [ 2 ] = g 2 ( Z [ 2 ] ) = σ ( Z [ 2 ] )
- Back propagation
dZ[2]=A[2]−Y d Z [ 2 ] = A [ 2 ] − Y
dw[2]=1mdZ[2](A[1])T d w [ 2 ] = 1 m d Z [ 2 ] ( A [ 1 ] ) T
db[2]=1mnp.sum(dZ[2], axis=1, keepdims=True) d b [ 2 ] = 1 m n p . s u m ( d Z [ 2 ] , a x i s = 1 , k e e p d i m s = T r u e )
dZ[1]=(w[2])TdZ[2]∗g[1] ′(Z[1]) d Z [ 1 ] = ( w [ 2 ] ) T d Z [ 2 ] ∗ g [ 1 ] ′ ( Z [ 1 ] )
dw[1]=1mdZ[1]XT d w [ 1 ] = 1 m d Z [ 1 ] X T
db[1]=1mnp.sum(dZ[1], axis=1, keepdims=True) d b [ 1 ] = 1 m n p . s u m ( d Z [ 1 ] , a x i s = 1 , k e e p d i m s = T r u e )
3.10 直观理解反向传播
- 解决掉矩阵的维度匹配问题就能杜绝很多bug。
- 上图仅为一个样本时。
dZ即 ∂L(a,y)∂z ∂ L ( a , y ) ∂ z
输入特征数量: n[0]=nx n [ 0 ] = n x
隐藏单元个数: n[1] n [ 1 ]
输出单元个数: n[2]=1 n [ 2 ] = 1
那么,
X−−>(n[0], m) X − − > ( n [ 0 ] , m )
W[1]、dW[1]−−>(n[1], n[0]) W [ 1 ] 、 d W [ 1 ] − − > ( n [ 1 ] , n [ 0 ] )
b[1] b [ 1 ] 、 db[1]−−>(n[1], 1) d b [ 1 ] − − > ( n [ 1 ] , 1 )
Z[1] Z [ 1 ] 、 dZ[1]−−>(n[1], m) d Z [ 1 ] − − > ( n [ 1 ] , m )
W[2]、dW[2]−−>(n[2], n[1]) W [ 2 ] 、 d W [ 2 ] − − > ( n [ 2 ] , n [ 1 ] )
b[2] b [ 2 ] 、 db[2]−−>(n[2], 1) d b [ 2 ] − − > ( n [ 2 ] , 1 )
Z[2] Z [ 2 ] 、 dZ[2]−−>(n[2], m) d Z [ 2 ] − − > ( n [ 2 ] , m )
dZ[1]=(w[2])TdZ[2]∗g[1] ′(Z[1]) d Z [ 1 ] = ( w [ 2 ] ) T d Z [ 2 ] ∗ g [ 1 ] ′ ( Z [ 1 ] ) 的维度分别为:
(n[1], m) ( n [ 1 ] , m ) = (n[1], n[2]) ( n [ 1 ] , n [ 2 ] ) (n[2], m) ( n [ 2 ] , m ) ∗(n[1], m) ∗ ( n [ 1 ] , m )
dw[1]=1mdZ[1]XT d w [ 1 ] = 1 m d Z [ 1 ] X T 的维度分别为:
(n[1], n[0]) ( n [ 1 ] , n [ 0 ] ) = (n[1], m) ( n [ 1 ] , m ) (m, n[0]) ( m , n [ 0 ] )
db[1]=1mnp.sum(dZ[1], axis=1, keepdims=True) d b [ 1 ] = 1 m n p . s u m ( d Z [ 1 ] , a x i s = 1 , k e e p d i m s = T r u e ) 的维度分别为: (n[1], 1) ( n [ 1 ] , 1 )
3.11 随机初始化
如果不对参数w进行随机初始化,比如全部设置为0,那么,可以证明,所有隐藏层单元都在计算相同的函数,呈对称状态,没有意义。
所以需要对w随机初始化。
一般都将w随机成很小的值。因为如果激活函数是sigmoid或者tanh这样的,小的输入有大的梯度。如果w太大,很可能学习速率很慢。或者隐藏层没有用sigmoid或者tanh,但是是二分类问题,输出层用到了sigmoid,那么也不希望初始参数太大。
b设置成0不影响,但一般也进行随机初始化。
第四周 深层神经网络
4.1 深层神经网络
算网络层数时候不算输入层。
4.2 深层神经网络的前向传播
Z[l]=w[l]A[l−1]+b[l] Z [ l ] = w [ l ] A [ l − 1 ] + b [ l ]
A[l]=g[l](Z[l]) A [ l ] = g [ l ] ( Z [ l ] )
4.3 核对 矩阵的维数
- 用一张纸算。
- w[l]、dw[l]−−>(n[l], n[l−1]) w [ l ] 、 d w [ l ] − − > ( n [ l ] , n [ l − 1 ] )
- b[l]、db[l]−−>(n[l], 1) b [ l ] 、 d b [ l ] − − > ( n [ l ] , 1 )
- A[l]、z[l]、dA[l]、dz[l]−−>(n[l], m) A [ l ] 、 z [ l ] 、 d A [ l ] 、 d z [ l ] − − > ( n [ l ] , m )
4.4 为什么使用深层表示
- 类脑;
- 深层比浅层能更容易描述一个复杂函数。
4.5 搭建深层神经网络块
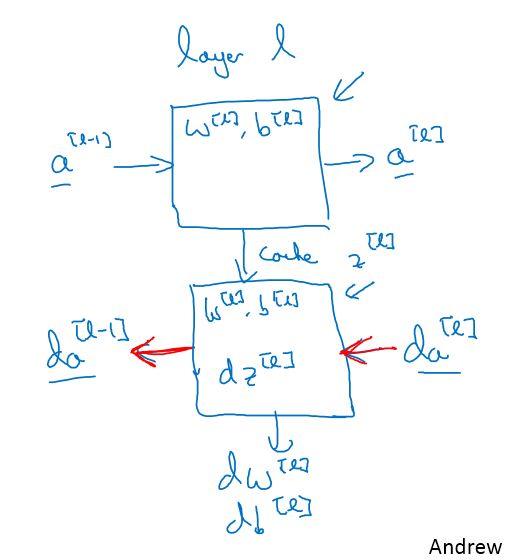
z[l] z [ l ] 会被缓存下来到反向传播的时候使用。
一次完整的梯度下降过程:
反向传播到最后不需要计算 da[0] d a [ 0 ]
4.6 前向传播和反向传播
- Forward propagation
输入: A[l−1] A [ l − 1 ]
输出: A[l] A [ l ]
缓存: Z[l]、w[l]、b[l] Z [ l ] 、 w [ l ] 、 b [ l ]
Z[l]=w[l]A[l−1]+b[l] Z [ l ] = w [ l ] A [ l − 1 ] + b [ l ]
A[l]=g[l](Z[l]) A [ l ] = g [ l ] ( Z [ l ] )
Back propagation
输入: dA[l] d A [ l ]
输出: dA[l−1] d A [ l − 1 ] 、 dw[l]、db[l] d w [ l ] 、 d b [ l ]
dZ[l]=dA[l]∗g[l] ′(Z[l]) d Z [ l ] = d A [ l ] ∗ g [ l ] ′ ( Z [ l ] )dw[l]=1mdZ[l](A[l−1])T d w [ l ] = 1 m d Z [ l ] ( A [ l − 1 ] ) T
db[l]=1mnp.sum(dZ[l], axis=1, keepdims=True) d b [ l ] = 1 m n p . s u m ( d Z [ l ] , a x i s = 1 , k e e p d i m s = T r u e )
dA[l−1]=(w[l])TdZ[l] d A [ l − 1 ] = ( w [ l ] ) T d Z [ l ]
4.7 参数 vs 超参数
- 参数:
- w[l]、b[l] w [ l ] 、 b [ l ]
- w[l]、b[l] w [ l ] 、 b [ l ]
超参数:
- 学习速率 α α
- 迭代次数 iterations
- 隐藏层的层数 L
- 隐藏单元数 n[l] n [ l ]
- 激活函数
- mini batch size
- momentum动量
- 几种不同的正则化参数。。。
- ……
超参数的选择,就是不断的尝试。
4.8 这和大脑有什么关系
没什么关系。
用神经元类比深度神经网络只是一个粗浅的类比。
一个神经元到底在干什么,没有人能够解释。
人到底是怎么学习的,也还是一个未解之谜。
深度学习是一个强大的工具,能学习到各种灵活、复杂的函数,来实现 x x 到 y y 的映射。
但和人类的学习比起来,不值一提。
