GAN生成对抗网络：数学原理

1. 极大似然估计

GAN用到了极大似然估计（MLE），因此我们对MLE作简单介绍。

MLE的目标是从样本数据中估计出真实的数据分布情况，所用的方法是最大化样本数据在估计出的模型上的出现概率，也即选定使得样本数据出现的概率最大的模型，作为真实的数据分布。

将真实模型用参数$\theta$表示，则在模型$\theta$下，样本数据的出现概率（likelihood）是$$\prod _{i=1}^m{p}_{model}(x_i;\theta )\text{\hspace{1em}(1)}$$

其中$x_i$表示样本中的第$i$个数据。

最大化(1)式的概率，求得满足条件的$\theta$：
$$\begin{array}{rl}{\theta }^{\ast }& =\arg \underset{\theta }{\max }\prod _{i=1}^m{p}_{model}(x_i;\theta )\\ & =\arg \underset{\theta }{\max }\sum _{i=1}^m\log p_{model}(x_i;\theta )\end{array}$$

还可以使用KL散度来代表MLE方法：
$$\begin{array}{rl}{\theta }^{\ast }& =\arg \underset{\theta }{\min }{D}_{KL}(p_{data}(x)||p_{model}(x;\theta )\\ & =\arg \underset{\theta }{\min }\left\{\sum _{i=1}^m{p}_{data}(x_i)\log p_{data}(x_i)-\sum _{i=1}^m{p}_{data}(x_i)\log p_{model}(x_i;\theta )\right\}\\ & =-\arg \underset{\theta }{\min }\sum _{i=1}^m{p}_{data}(x_i)\log p_{model}(x_i;\theta )\\ & =\arg \underset{\theta }{\max }\sum _{i=1}^m{p}_{data}(x_i)\log p_{model}(x_i;\theta )\end{array}$$

在实际上，我们无法得到数据的真实分布$p_{data}$，但是可以从$m$个数据的样本中近似得到一个估计${\hat{p}}_{data}$。

为了便于理解KL散度，我们在下面对其进行简要介绍。

2. 相对熵，KL散度

两个概率分布$P$和$Q$的KL散度定义如下：
$$D_{KL}(P||Q)=\sum _{i}P(i)\log \frac{P(i)}{Q(i)}$$

性质：
$$D_{KL}(P||Q)\ge 0$$

当且仅当$P=Q$时，等号成立。（证明过程借用吉布斯不等式：${\sum }_i{p}_i\log p_i\ge {\sum }_i{p}_i\log q_i$，证明吉布斯不等式会用到关系$\log x\le x-1$）

KL散度反映了两个分布$P$和$Q$的相似情况，KL散度越小，两个分布越相似。

KL散度是不对称的：
$$D_{KL}(P||Q)̸=D_{KL}(Q||P)$$

3. KL散度与交叉熵的关系

神经网络中常常使用交叉熵作为损失函数：
$$L=-\sum _i{y}_i\log h_i$$

其中$y_i$是实际的标签值，$h_i$是网络的输出值。

我们将$y$和$h$的KL散度展开，得到：
$$\begin{array}{rl}{D}_{KL}(y||h)& =\sum _i{y}_i\log \frac{y_i}{h_i}\\ & =\sum _i{y}_i\log y_i-\sum _i{y}_i\log h_i\\ & =\sum _i{y}_i\log y_i+L\\ & =Constant+L\end{array}$$

因此，最小化KL散度，等价于最小化损失函数$L$。也即交叉熵损失函数反应的是网络输出结果和样本实际标签结果的KL散度的大小，交叉熵越小，KL散度也越小，网络的输出结果越接近实际值。

4. JS散度

对于两个分布$P$和$Q$，JS散度是：
$$D_{JS}(P||Q)=\frac{1}{2}{D}_{KL}(P||\frac{P+Q}{2})+\frac{1}{2}{D}_{KL}(Q||\frac{P+Q}{2})$$

JS散度是对称的，并且有界$[0,\log 2]$。

5. GAN 框架

生成器，生成与训练集数据相同分布的样本；判别器，检查生成器生成的样本是真的还是假的。
The generator is trained to fool the discriminator.

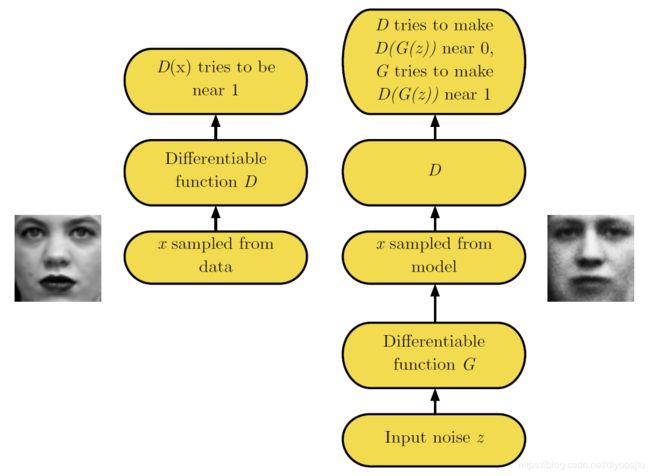
判别器的损失函数

判别器的损失函数为：
$$J^{(D)}({\theta }^{(D)},{\theta }^{(G)})=-\frac{1}{2}{\mathbb{E}}_{x\sim p_{data}}\log D(x)-\frac{1}{2}{\mathbb{E}}_{z\sim p_{model}}\log (1-D(G(z)))\text{\hspace{1em}(2)}$$

上式其实就是一个交叉熵损失函数。GAN的判别器在训练的过程中，数据集包含两个部分，一部分是训练集的样本$x$，对应的标签$y=1$，一部分是生成器生成的数据$G(z)$，对应的标签$y=0$，因此判别器的训练集可以看做$X=\{x,G(z)\},Y=\{1,0\}$。

训练集样本是$X$，标签是$Y$，网络输出是$H$，则交叉熵损失函数为：
$$J=\frac{1}{m}\sum _{i=1}^m\{-Y_i\log H_i-(1-Y_i)\log (1-H_i)\}\text{\hspace{1em}(3)}$$

与式(2)作比较，前一项的$\log H$等价于式(2)中的$\log D(x)$，后一项的$\log (1-H_i)$等价于式(2)中的$\log (1-D(G(z)))$。将$x$看做包含了真实样本和生成器生成的数据$G(z)$的新的训练集，则判别器的损失函数可以重新写作：
$$\begin{array}{rl}{J}^{(D)}({\theta }^{(D)},{\theta }^{(G)})& =-\frac{1}{2}{\mathbb{E}}_{x\sim p_{data}}\log D(x)-\frac{1}{2}{\mathbb{E}}_{x\sim p_{model}}\log (1-D(x))\\ & =-\frac{1}{2}\sum _i{p}_{data}(x_i)\log D(x_i)-\frac{1}{2}\sum _i{p}_{model}(x_i)\log (1-D(x_i))\end{array}\text{\hspace{1em}(4)}$$

对上式关于$D(x)$求导，并令导数为0，得到：
$$D^{\ast }(x)=\frac{p_{data}(x)}{p_{data}(x)+p_{model}(x)}$$

生成器的损失函数

令$J^{(G)}=-J^{(D)}$，则
$$\begin{array}{rl}{J}^{(G)}({\theta }^{(D)},{\theta }^{(G)})& =\frac{1}{2}{\mathbb{E}}_{x\sim p_{data}}\log D(x)+\frac{1}{2}{\mathbb{E}}_{z\sim p_{model}}\log (1-D(G(z)))\\ & =Constant+\frac{1}{2}{\mathbb{E}}_{z\sim p_{model}}\log (1-D(G(z)))\end{array}$$

生成器没有直接接受任何的训练集数据，训练集数据的信息是通过判别器学习后传递过来的。