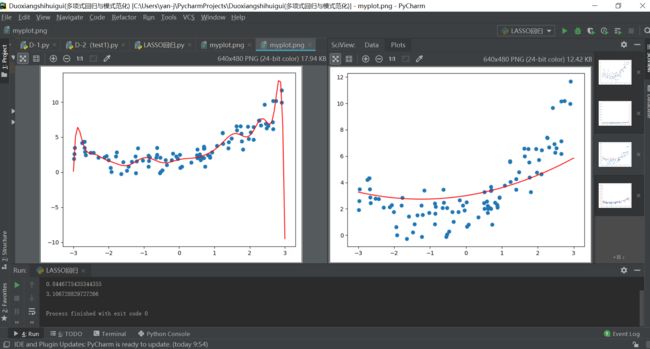
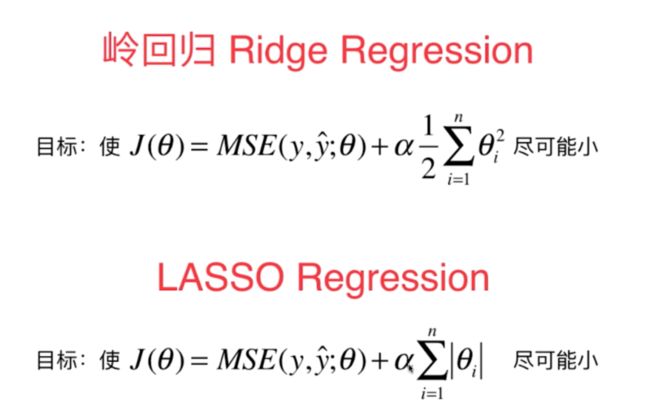机器学习的模型泛化
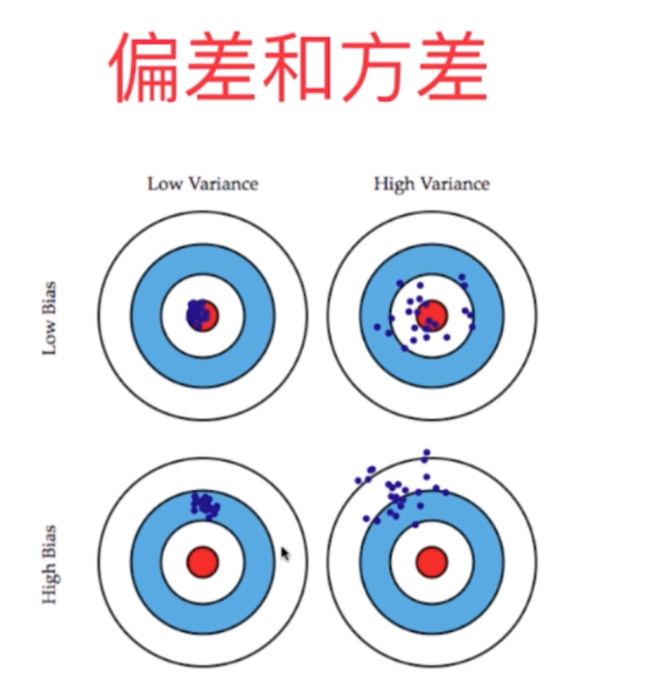
1、机器学习的模型误差主要含有三个方面的误差:模型偏差、模型方差以及不可避免的误差。
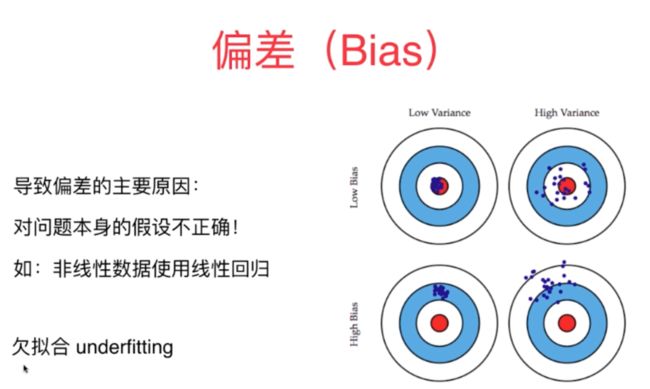
2、对于机器学习训练模型的偏差主要因为对于问题本身的假设不对,比如非线性误差假设为线性误差进行训练和预测,算法层面上欠拟合是产生较大偏差的主要原因。另外主要来自于特征参量与最终结果的相关性,如果相关性很低或者高度不相关的话也会导致较大的偏差。
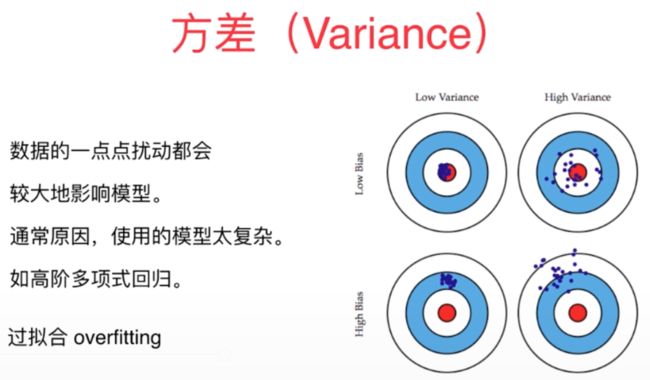
3、对于机器学习模型的方差主要是来自于数据的扰动以及模型的过于复杂,在算法层面上过拟合是引起模型方差较大的主要原因,因为过拟合会导致整体模型的复杂度太高,从而引起方差很大。
4、对于不同的算法其存在误差种类是不同的,有些算法是天生的高方差算法,比如KNN算法,非参数算法一般都是高方差算法,因为它不对问题的前提进行假设。有些算法天生是高偏差的算法,比如线性回归算法,参数学习算法一般都属于高偏差算法,因为它对数据具有极强的假设。
5、大多数算法都可以通过调节其中的超参数调整模型的方差和偏差,并且一般情况下模型的方差和偏差是矛盾的,降低偏差,会增大方差,降低方差,也会增大偏差。
6、机器学习的主要挑战主要来自于方差,当然这样的结论主要局限于算法层面,解决机器学习算法模型的方差的主要方式有以下几个方面:
(1)降低模型的复杂度;
(2)减小数据的维度:PCA算法进行降维和降噪;
(3)增加数据的样本数;
(4)评测算法的准确度时需要采用验证集,即使用交叉验证方式;
(5)模型的正则化。
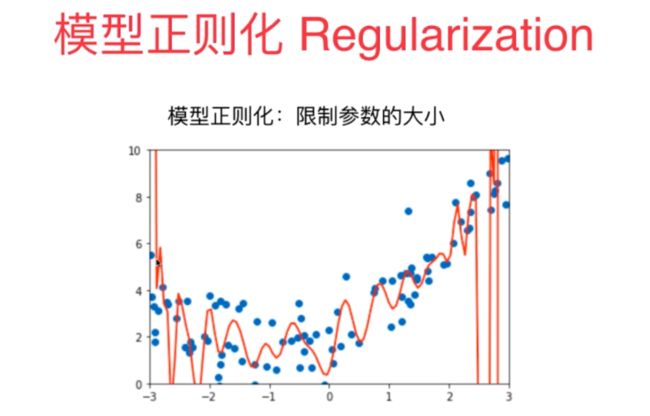
7、模型的正则化主要是指对于复杂的模型的特征参数的系数进行一定的限制,使其不要太大,采取的方式主要是改变损失函数,在损失函数中加入模型的正则化项,从而在使得损失函数最最小时限制相应的参数的大小.
图 正则函数表达式
8、具体来讲,模型的正则化主要含有两种方式:岭回归Ridge Regression和LASSO Regression,两者的损失函数表达式有所不同,这也造成了两者在超参数a从0增大到正无穷时各项特征系数变化以及拟合模型曲线变化的不同特点。
图
(1)Ridge模型:因为其损失函数后面添加项的梯度变化的连续性,所以当它的超参数alhpa不断增大时,它的各项特征系数是连续慢慢地趋向于0的;因此它的拟合结果始终是一种光滑的曲线形式。
(2)LASSO模型:因为后面损失函数添加项是一个绝对值函数,因此在梯度下降法求取最小值时,它的导数是一个阶跃函数sign(x),因此,当超参数a不断增大时,其theta各项特征系数中会有一部分趋向于变为0,这也使得LASSO模型可以用来做特征选用。它的拟合结果随着超参数a的增大,会越来越趋近于一条直线,这也说明特征参数的部分系数会变为0.
图注:左边为Ridge岭回归结果,右边为LASSO回归结果
9、弹性网:弹性网是一种复合型的正则化方式,它是在损失函数的基础上既添加了岭回归的L1正则项,又添加了LASSO回归的正则化项L2正则项,包含了岭回归和LASSO回归的综合优点,其具体的数学表达式如下:

10、模型正则化的两种算法模型岭回归和LASSO回归正则化的实现代码具体如下:
#(1)使用岭回归的正则化方式减小模型方差,将其封装为一个函数
import numpy as np
import matplotlib.pyplot as plt
x=np.random.uniform(-3,3,size=100)
X=x.reshape(-1,1)
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(X,y,random_state=666)
from sklearn.linear_model import Ridge
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error
def Ridgeregression(degree,alpha):
return Pipeline([("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("Ridge_reg", Ridge(alpha=alpha))
])
r1=Ridgeregression(20,10000)
r1.fit(x_train,y_train)
y11=r1.predict(x_test)
print(mean_squared_error(y11,y_test))
plt.figure()
plt.scatter(X,y)
x1=np.linspace(-3,3,100).reshape(100,1)
y1=r1.predict(x1)
plt.plot(x1,y1,"r")
#plt.axis([-3,3,-1,10])
plt.show()
#(2)使用LASSO回归的正则化方式减小模型方差,将其封装为一个函数
#采用LASSO回归进行训练和预测
from sklearn.linear_model import Lasso
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error
def lassoregression(degree,alpha):
return Pipeline([("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("LASSO_reg", Lasso(alpha=alpha))
])
LA1=lassoregression(20,1) #当a的值从0开始增大时,其拟合曲线的模型会越来越平直,慢慢会接近一条直线,区别于岭回归的曲线,这是由LASSO正则化数学式子决定的
LA1.fit(x_train,y_train)
y11=LA1.predict(x_test)
print(mean_squared_error(y11,y_test))
plt.figure()
plt.scatter(X,y)
x1=np.linspace(-3,3,100).reshape(100,1)
y1=LA1.predict(x1)
plt.plot(x1,y1,"r")
#plt.axis([-3,3,-1,10])
plt.show()
#(3)采用普通多项式回归进行预测
import numpy as np
import matplotlib.pyplot as plt
x=np.random.uniform(-3,3,size=100)
X=x.reshape(-1,1)
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(X,y,random_state=666)
from sklearn.linear_model import Ridge
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
def polynomialRegression(degree):
return Pipeline([("poly",PolynomialFeatures(degree=degree)),
("std_scaler",StandardScaler()),
( "lin_reg",LinearRegression())
])
poly2_reg=polynomialRegression(20)
poly2_reg.fit(X,y)
y2=poly2_reg.predict(X)
print(mean_squared_error(y,y2))
print(poly2_reg.score(X,y))
plt.figure()
plt.scatter(X,y)
x1=np.linspace(-3,3,100).reshape(100,1)
y11=poly2_reg.predict(x1)
plt.plot(x1,y11,"r")
#plt.axis([-3,3,-1,10])
plt.show()
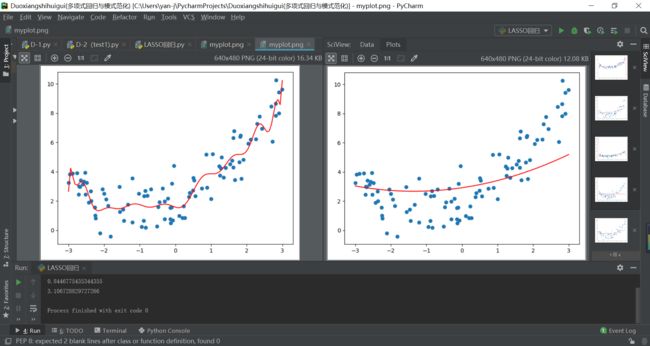
注:左为岭回归方式,右为普通多项式回归方式
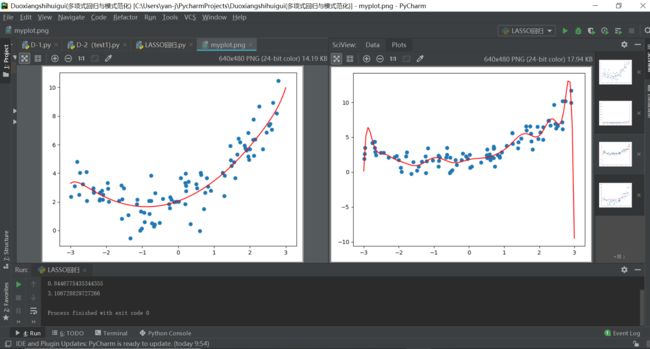
注:左为普通多项式回归,右为LASSO回归方式