今天在工作中遇到这样一个问题:给定1个矩形,左下角的点point(x, y),长w,高h,要在这个矩形里随机出n个不同的点用来种怪。这个算法该怎么写呢?这对于我来说确实成为了一个问题。图示如下:
由于任务时间紧,做的又是Demo的原因,我不假思索的写出了下面这个算法:
//从[from, to]区间中随机一个整数 function randomInt (from, to) { //方法实现就不写了 }
function randomCoords (point, w, h, n) { //目的数组 var coords = []; var map = {}; var count = n; if ((w + 1) * (h + 1) < n) { count = (w + 1) * (h + 1); } while (count > 0) { var x = randomInt(point.x, point.x + w); var y = randomInt(point.y, point.y + h); //已经随机出该点,就丢掉 if (map[x] && map[x][y]) continue; if (!map[x]) map[x] = {}; map[x][y] = true; coords.push({x:x, y:y}); count --; }
return coords;
}
这个算法着实太笨了,当时也没有细想。等把任务完成了,我发现离下班的时间还有很长一段时间。因为制度上要求要加班,我只能忍了。我想,如果被别人看到我写的这么一个垃圾算法,那他肯定认为我实在太Low了。所以,我开始认真思索这个问题。
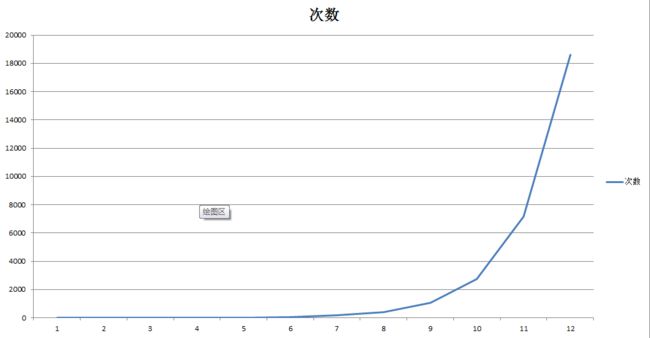
先不考虑优化的算法该如何实现,我想先了解一下这个算法到底有多Low。我假设了一种情况,长和高都是5,然后把所有点都随机出来,需要的平均次数是多少呢?答案是:5/5 * 5/4 * 5/3 * 5/2 * 5/1 = 26.04166667。还好,不是很多次,还能承受。然后我把5改成n做成一个图表,图表如下:
当n=10的时候,就需要循环2000多次;而当n=12的时候,就得需要循环18000多次了。图表是不是很吓人,我反正是惊呆了。这绝对不行,如果是做项目的时候要这样写,我肯定已经被老板骂死了。
那该怎么改呢?我马上就想到了一个改进的方法。如果要随机的点数超出一半点数的话,我就随机出不用的点来,那么剩下的点就是我要的点了。这个想法其实很好,但是要结合上面的算法用的话,其实还不是很好。
那么到底该怎么实现呢?我开始从问题本质考虑。一般情况下,随机分为两种,放回抽样随机和不放回抽样随机,它们随机所需要的次数都是n次,只不过不放回抽样需要把已经随机出来的元素从样本库里拿出来。
很显然,这个问题是不放回抽样随机。那么又该怎么把已经随机出来的元素从样本库里拿出来呢?有一种代码里常用的方法,就是构建一个样本库的数组,然后再从数组里把那个元素拿出来。这样的确可以避免随机次数成近似指数级增长。它构建样本库数组的增长曲线是平方级,一般情况下是服务器可以接受的。但是如果要在手机等移动设备上执行的话,我们就要精益求精了。那么有没有更好的算法呢?当然有。
我就不废话了,说一下我最终是如何实现的:
1、求出矩形中所拥有的点数totalNum;
2、在[0, totalNum-1]区间中随机出一个数字来,然后把该数字按一定规则对应到矩形中的某个点上,然后totalNum减1;
3、随机n次,得到所有随机点。
这里最关键的是第二步,要实现它需要做到如下两点:
1、指定数字到(x,y)坐标的映射规则。我采用的是x=point.x+rand%(w+1); y=point.y+Math.floor(rand/(w+1));
2、设置map,其key值是已经随机出的数字,其value值是最近一次随机出该数字时随机区间的末尾数字,即totalNum-1。我管这种方法叫尾数置换。其图示如下:
废话不多说了,代码呈上:
function randomCoords (point, w, h, n) { var coords = []; var map = {}; var totalNum = (w + 1) * (h + 1); var num = n; if (totalNum < n) { num = totalNum; } while (coords.length < num) { //在区间[0, totalNum-1]区间里随机 var randRaw = utils.random_int(0, totalNum - 1); //求出有效值并计算出坐标值 var rand = map[randRaw] === undefined ? randRaw : map[randRaw]; var x = point.x + rand % (w + 1); var y = point.y + Math.floor(rand / (w + 1)); coords.push({x:x, y:y}); //更新置换尾数和区间 totalNum --; map[randRaw] = totalNum; } return coords; }
这个算法的时间复杂度是O(n)级的,远小于前面两种算法。而且它还可以优化,思路前面已经给出来了,就是当要随机的点数超出总点数一半的时候,就随机出不需要的点数,然后剩下的点就是所要求的点了。思路很简单,代码我就不在这里写了。