搜索的策略（2）——贪心策略

贪心策略

　　很多时候，我们只需要找到问题的最优解，如果使用盲目搜索策略，就必须先找出所有解，再进一步比较哪个是最优的，当在解空间十分庞大时，难免有些浪费体力的感觉。这时候，不妨试试更高效的贪心策略。

　　贪心策略也叫贪心算法（greedy algorithm）或贪婪算法，是一种强有力的穷举搜索策略，它通过一系列选择来找到问题的最优解。在每个决策点，它都会做出当时看来是最优的选择，一旦选择后就无需回溯。简单来说，贪心策略是一种“步步为营”的策略——只要做好眼前的每一步，就自然会在未来得到最好的结果，并且做过的决策就是是最好的决策，无需再次检查。

　　很多时候，贪心法并不能保证得到最优解，它能得到的是较为接近最优解的较好解，因此贪心法经常被用来解决一些对结果精度要求不高的问题。

小偷的背包

　　一个小偷撬开了一个保险箱，发现里面有N个大小和价值不同的东西，但自己只有一个容量是M的背包，小偷怎样选择才能使偷走的物品总价值最大？

　　假设有5个物品A,B,C,D,E，它们的体积分别是3,4,7,8,9，价值分别是4,5,10,11,13，可以用矩形表示体积，将矩形旋转90°后表示价值：

　　下图展示了一个容量为17的背包的4中填充方式，其中有两种方式的总价都是24：

　　背包问题有很多重要的实应用，比如长途运输时，需要知道卡车装载物品的最佳方式。

搜索策略

　　我们基于贪心策略去解决背包问题：在取完一个物品后，找到填充背包剩余部分的最佳方法。对于一个容量为M的背包，需要对每一种类型的物品都推测一下，如果把它装入背包的话总价值是多少，依次递归下去就能找到最佳方案。这个方案的原理是，一旦做出了最佳选择就无需更改，也就是说一旦知道了如何填充较小容量的背包，则无论下一个物品是什么，都无需再次检验已经放入背包中的物品（已经放入背包中的物品一定是最佳方案）。

寻找解决方案

　　首先定义物品的数据模型：

1 class Goods:
2     ''' 物品的数据结构  '''
3     def __init__(self, size, value):
4         '''
5         :param size: 物品的体积
6         :param value: 物品的价值
7         '''
8         self.size = size
9         self.value = value

　　然后使用fill_into_bag方法寻找最佳填充方案。该方法接收背包容量和物品清单两个参数，返回背包最大价值和最佳填充方案：

 1 def fill_into_bag(M, goods_list):
 2     '''
 3     填充一个容量是 M 的背包
 4     :param M: 背包的容量
 5     :param goods_list: 物品清单，包括每种物品的体积和价值，物品互不相同
 6     :return: (最大价值，最佳填充方案)
 7     '''
 8     space = 0       # 背包的剩余容量
 9     max = 0         # 背包中物品的最大价值
10     plan = []       # 最佳填充方案
11
12     for goods in goods_list:
13         space = M - goods.size
14         if space >= 0:
15             # 在取完一个物品（goods）后，填充背包剩余部分的最佳方法
16             space_plan = fill_into_bag(space, goods_list)
17             if space_plan[0] + goods.value > max:
18                 max = space_plan[0] + goods.value
19                 plan = [goods] + space_plan[1]
20
21     return max, plan

　　最后可以看看小偷应该怎样填充背包：

 1 def paint(plan):
 2     print('最大价值：' + str(plan[0]))
 3     print('最佳方案：')
 4     for goods in plan[1]:
 5         print('\t大小：{0}\t价值：{1}'.format(goods.size, goods.value))
 6
 7 if __name__ == '__main__':
 8     goods_list = [Goods(3, 4), Goods(4, 5), Goods(7, 10), Goods(8, 11), Goods(9, 13)]
 9     plan = fill_into_bag(17, goods_list)
10     paint(plan)

　　运行结果：

　　遗憾的是，fill_into_bag方法只能作为一个简单的试验样品，它犯了一个严重的错误——第二次递归会忽略上一次所做的所有计算！这将导致要花指数级的时间才能计算出结果。为了把时间降为线性，需要使用动态编程技术对其进行改进，把计算过的值都缓存起来，由此得到了背包问题的2.0版：

 1 # 字典缓存，space:(max,plan)
 2 sd = {}
 3 def fill_into_bag_2(M, goods_list):
 4     '''
 5     填充一个容量是 M 的背包
 6     :param M: 背包的容量
 7     :param goods_list: 物品清单，包括每种物品的体积和价值，物品互不相同
 8     :return: (最大价值，最佳填充方案)
 9     '''
10     space = 0       # 背包的剩余容量
11     max = 0         # 背包中物品的最大价值
12     plan = []       # 最佳填充方案
13
14     if M in sd:
15         return sd[M]
16
17     for goods in goods_list:
18         space = M - goods.size
19         if space >= 0:
20             # 在取完一个物品（goods）后，填充背包剩余部分的最佳方法
21             print(goods.size, space)
22             space_plan = fill_into_bag_2(space, goods_list)
23             if space_plan[0] + goods.value > max:
24                 max = space_plan[0] + goods.value
25                 plan = [goods] + space_plan[1]
26     # 设置缓存，M空间的最佳方案
27     sd[M] = max, plan
28
29     return max, plan

　　这次可以快速运行了，当然，我们并不想把这个算法告诉小偷。

骑士旅行

　　骑士旅行（Knight tour）问题是另一个关于国际象棋的话题：骑士可以由棋盘上的任一个方格出发，如果每个方格只能到达一次，它要如何走完所有的位置？骑士旅行曾在十八世纪初倍受数学家与拼图迷的注意，具体什么时候被提出已不可考。

　　“骑士”的走法和吃子都和中国象棋的“马”类似，遵循“马走日”的原则，只不过没有“蹩腿”的约束：

　　在国际象棋中，骑士的价值为3，虽然不算高，却灵活、易调动、易双抽，从这一点看，它的价值不亚于皇后。

5.5.1 构建数据模型

　　我们依然使用8×8的二维列表存储棋盘信息，用0表示方格的初始状态。使用一个从1开始的计数器记录骑士旅行的轨迹，每走一步，计数器加1，同把骑士到达的方格状态设置为计数器的值，这些数值就是骑士的旅程轨迹：

　　骑士从一个方格出发， 最多可以向八个方向行进，怎样方便地表示这八个方向呢？我们都见识或棋谱，在棋谱上，把骑士可以到达的八个方格依次编号：

　　这像极了平面直角坐标系，可以把棋盘外围的列序号看作y轴的坐标，行序号看作x轴的坐标，这样棋盘上的每一个方格就可以用一个二维向量表示，向量的第一个分量是行号，第二个分量是列号。这实际上是把我们熟知的直角坐标系顺时针旋转了90°，目的是为了能够更方便地用二维列表表示。

　　骑士的初始位置是(3,3)，从这里出发可以到达的另外八个位置依次是：(2,1)，(1,2)，(1,4)，(2,5)，(4,5)，(5,4)，(5,2)，(4,1)。它们与初始位置的差值是：(-1,-2)，(-2,-1)，(-2,1)，(-1,2)，(1,2)，(2,1)，(2,-1)，(1,-2)。由于向量是表示大小和方向的量，与具体位置无关，所以骑士从任意位置出发，加上差值向量后都可以到达另外八个位置（不考虑棋盘边界）。以上图为例：

　　用一个列表存储这些差值向量。骑士旅行的数据模型：

 1 class KnightTour:
 2     def __init__(self):
 3         # 棋盘的行数和列数
 4         self.row_num, self.col_num = 8, 8
 5         # 方格的初始状态
 6         self.s_init = 0
 7         # 棋盘
 8         self.chess_board = [[self.s_init] * self.row_num for i in range(self.row_num)]
 9         # 差值向量，表示骑士移动的八个方向
10         self.v_move = [(-1, -2), (-2, -1), (-2, 1), (-1, 2), (1, 2), (2, 1), (2, -1), (1, -2)]
11         # 计数器终点
12         self.max = self.row_num * self.col_num
13         # 解决方案
14         self.answer = None

盲目的深度优先策略

　　大概最容易想到的旅行方法就是深度优先搜索，基本思虑和八皇后类似：骑士从一个位置开始，向一个方向探索，无法继续前进时就“悔棋”，尝试下一个方向，如果计数器能累加到64，说明骑士可以完成旅行：

 1 import copy
 2
 3 class KnightTour:
 4     ……
 5     def enable(self, curr_board, x, y):
 6         ''' 判断x,y位置是否可走 '''
 7         # 边界条件判断 and x,y位置是否曾经到达过
 8         return (0 <= x < self.col_num and 0 <= y < self.row_num) and curr_board[x][y] == self.s_init
 9
10     def move(self, curr_board, x, y, count):
11         '''
12         骑士从(x,y)位置开始旅行
13         :param curr_board: 当前棋盘
14         :param x: 起始位置行号
15         :param y: 起始位置列号
16         :param count: 当前计数
17         :return
18         '''
19         # 找到一种方法就退出
20         if self.answer is not None:
21             return
22         # 如果已经走遍了所有方格，该问题解决
23         if count > self.max:
24             self.answer = curr_board
25             return
26
27         if self.enable(curr_board, x, y):
28             curr_board[x][y] = count
29             # 继续旅行,分别探测八个方向
30             for v_x, v_y in self.v_move:
31                 # 复制棋盘上的状态, 以便回溯
32                 bord = copy.deepcopy(curr_board)
33                 self.move(bord, x + v_x, y + v_y, count + 1)

　　这里x是方格的行序号，y是方格列序号。Enable方法用于判断(x,y)是否超出的棋盘边界，同时也检查了骑士是否已经到访过(x,y)。move方法以递归的方式向下一步探索。悔棋的回溯操作使用了复制棋盘状态的方式，这需要大量的内存，它有一个通过更改方格状态的代替版本：

 1  def move2(self, x, y, count):
 2         '''
 3        骑士从(x,y)位置开始旅行
 4        :param x: 起始位置行号
 5        :param y: 起始位置列号
 6        :param count: 当前计数
 7        :return
 8         '''
 9         # 找到一种方法就退出
10         if self.answer is not None:
11             return
12         # 如果已经走遍了所有方格，该问题解决
13         if count > self.max:
14             self.answer = copy.deepcopy(self.chess_board)
15             return
16
17         if self.enable(self.chess_board, x, y):
18             self.chess_board[x][y] = count
19             # 继续旅行,分别探测八个方向
20             for v_x, v_y in self.v_move:
21                 self.move2(x + v_x, y + v_y, count + 1)
22             # 将该位置设为初始值，以便悔棋
23             self.chess_board[x][y] = self.s_init

　　move2只使用了一个棋盘，为了回到上一个方格，当骑士探索完八个方向后，需要将当前所在方格重置为初始状态。move2的改进仅仅是节省了一点内存，和move1并没有本质的区别，它们在运行时都相当缓慢。骑士每到达一个位置后，都将向八个方向探索，棋盘上共有64个方格，探索的数量也会产生爆炸，因此我们在找到一种方案后就马上退出。

　　完整代码：

 1 import copy
 2
 3 class KnightTour:
 4     def __init__(self):
 5         # 棋盘的行数和列数
 6         self.row_num, self.col_num = 8, 8
 7         # 方格的初始状态
 8         self.s_init = 0
 9         # 棋盘
10         self.chess_board = [[self.s_init] * self.row_num for i in range(self.row_num)]
11         # 差值向量，表示骑士移动的八个方向
12         self.v_move = [(-1, -2), (-2, -1), (-2, 1), (-1, 2), (1, 2), (2, 1), (2, -1), (1, -2)]
13         # 计数器终点
14         self.max = self.row_num * self.col_num
15         # 解决方案
16         self.answer = None
17
18     def start(self, x, y):
19         '''
20          旅行开始
21         :param x: 起始位置行号
22         :param y: 起始位置列号
23         :return:
24         '''
25         # self.move(self.chess_board, x, y, 1)
26         self.move2(x, y, 1)
27
28     def enable(self, curr_board, x, y):
29         ''' 判断x,y位置是否可走 '''
30         # 边界条件判断 and x,y位置是否曾经到达过
31         return (0 <= x < self.col_num and 0 <= y < self.row_num) and curr_board[x][y] == self.s_init
32
33     def move(self, curr_board, x, y, count):
34         '''
35         骑士从(x,y)位置开始旅行
36         :param curr_board: 当前棋盘
37         :param x: 起始位置行号
38         :param y: 起始位置列号
39         :param count: 当前计数
40         :return
41         '''
42         # 找到一种方法就退出
43         if self.answer is not None:
44             return
45         # 如果已经走遍了所有方格，该问题解决
46         if count > self.max:
47             self.answer = curr_board
48             return
49
50         if self.enable(curr_board, x, y):
51             curr_board[x][y] = count
52             # 继续旅行,分别探测八个方向
53             for v_x, v_y in self.v_move:
54                 # 复制棋盘上的状态, 以便回溯
55                 bord = copy.deepcopy(curr_board)
56                 self.move(bord, x + v_x, y + v_y, count + 1)
57
58     def move2(self, x, y, count):
59         '''
60        骑士从(x,y)位置开始旅行
61        :param x: 起始位置行号
62        :param y: 起始位置列号
63        :param count: 当前计数
64        :return
65         '''
66         # 找到一种方法就退出
67         if self.answer is not None:
68             return
69         # 如果已经走遍了所有方格，该问题解决
70         if count > self.max:
71             self.answer = copy.deepcopy(self.chess_board)
72             return
73
74         if self.enable(self.chess_board, x, y):
75             self.chess_board[x][y] = count
76             # 继续旅行,分别探测八个方向
77             for v_x, v_y in self.v_move:
78                 self.move2(x + v_x, y + v_y, count + 1)
79             # 将该位置设为初始值，以便悔棋
80             self.chess_board[x][y] = self.s_init
81
82     def display(self):
83         if self.answer is None:
84             print('No answers!')
85             return
86
87         for row in  self.answer:
88             for c in row:
89                 print('%4d' % c, end='')
90             print()
91
92 if __name__ == '__main__':
93     kt = KnightTour()
94     kt.start(7, 7)
95     kt.display()

　　如果骑士从(7, 7)出发，是能够完成旅行的：

　　骑士的初始位置和探测方向的顺序都会对运算时间产生极大的影响，如果把起始位置改成(0,0)，那么上面的程序将运行相当长的时间。

　　并不是在所有棋盘都能完成旅行，在3×3的棋盘上，骑士永远都无法到达中心位置：

带有预见性的贪心策略

　　由于每步试探的随机性和盲目性，使得基于深度优先策略的盲目搜索效率低下。如果能够找到一种克服这种随机性和盲目性的办法，按照一定规律选择前进的方向，则成功的可能性将大大增加。J.C. Warnsdorff在1823年提出一个聪明的解法：有选择地走下一步，先将最难的位置走完，既然每一格迟早都要走到，与其把困难留在后面，不如先走困难的路，这样后面的路才会宽阔，成功的机会也增大。

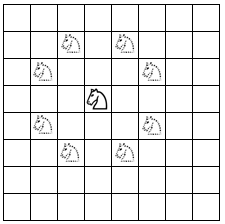
　　为了简单起见，我们的骑士先在5×5的棋盘上旅行。他的初始位置是(0,0)，这也是旅途的第一站，用“①”表示：

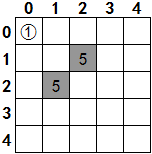
　　骑士的下一站只可能有两个，(1,2)和(2,1)，用深色方格表示：

　　如果骑士的下一站是(1,2)，那么从(1,2)出发，再下一站能够到达(0,4)，(2,4)，(3,3)，(3,1)，(2,0)这5个位置，将数字5标记在(1,2)中，用于表示路的宽窄，数字越小，路越窄，表示这条路线越困难。如果从(2,1)出发，再下一站能够到达另外五个位置：

　　第二站的“宽度”都是5。我们已经在图5.13中为八个方向编好了序号，从位于十点钟方向的1号开始，按照顺时针顺序逐一探索，选择最窄目的地当中的第一个作为下一站。按照这种方式，这里选择(1,2)作为下一站，并为该方格标记序号：

　　接下来从位置②继续探测，寻找最窄的第三站：

　　每个方格只能到达一次，所以不能再回到①，这也是贪心法和深度优先搜索的重要原因之一——在贪心法中，每一步决策都是当下最好的，一旦做出选择就不再回溯。从位置②出发，到达的最窄第三站是(0,4)：

　　按照这种方式继续向前探测，骑士最终能够顺利完成旅程：

　　按照这种思路使用贪心策略编写代码：

 1 class KnightTourGreedy:
 2     def __init__(self):
 3         # 棋盘的行数和列数
 4         self.row_num, self.col_num = 8, 8
 5         # 方格的初始状态
 6         self.s_init = 0
 7         # 棋盘
 8         self.chess_board = [[self.s_init] * self.row_num for i in range(self.row_num)]
 9         # 差值向量，表示骑士移动的八个方向
10         self.v_move = [(-1, -2), (-2, -1), (-2, 1), (-1, 2), (1, 2), (2, 1), (2, -1), (1, -2)]
11         # 计数器终点
12         self.max = self.row_num * self.col_num
13         # 解决方案
14         self.answer = None
15
16     def enable(self, x, y):
17         ''' 判断x,y位置是否可走 '''
18         # 边界条件判断 and x,y位置是否曾经到达过
19         return 0 <= x < self.col_num and 0 <= y < self.row_num and self.chess_board[x][y] == self.s_init
20
21     def get_width(self, x, y):
22         '''  x,y位置的“宽度”,数值越小，后面的路越窄  '''
23         # 如果（x, y）位置曾经达到过，返回9（比八个方向多1）
24         if self.enable(x, y) == False:
25             return 9
26         n = 0
27         for v_x, v_y in self.v_move:
28             if self.enable(x + v_x, y + v_y):
29                 n += 1
30         return n
31
32     def find_min(self, x, y):
33         ''' 找到从(x,y)出发，路“最窄”的下一个位置（下一个位置可到达的“未曾到访”方格数最少）  '''
34         min_x, min_y, min_n = -1, -1, 100
35         for v_x, v_y in self.v_move:
36             n = self.get_width(x + v_x, y + v_y)
37             if n < min_n:
38                 min_x, min_y, min_n = x + v_x, y + v_y, n
39         return min_x, min_y
40
41     def move(self, x, y, count):
42         ''' 骑士从(x,y)位置开始旅行  '''
43         # 找到一种方法就退出
44         if self.answer is not None:
45             return
46         # 如果已经走遍了所有方格，该问题解决
47         if count > self.max:
48             self.answer = self.chess_board
49             return
50
51         if self.enable(x, y):
52             self.chess_board[x][y] = count
53             # 找出八个方向中，路“最窄”的一个
54             next_x, next_y = self.find_min(x, y)
55             # 向路“最窄”的方向继续前进
56             self.move(next_x, next_y, count + 1)
57
58     def start(self, x, y):
59         ''' 旅行开始 '''
60         self.move(x, y, 1)
61
62     def display(self):
63         if self.answer is None:
64             print('No answers!')
65             return
66
67         for row in self.answer:
68             for c in row:
69                 print('%4d' % c, end='')
70             print()
71
72 if __name__ == '__main__':
73     kt = KnightTourGreedy()
74     kt.start(0, 0)
75     kt.display()

　　KnightTourGreedy的基本数据模型、棋盘边界判断和打印方法都和KnightTour一致。get_width用于计算从(x,y)位置的宽度，数值越小，该位置后面的路越“窄”，越难以到达。

　　对于路的宽窄来说，最窄是0，表示无路可走；最大是8，可以向8个方向前进（不能回到出发的位置）。为了让更便于find_min方法选择“最窄”的路，如果(x,y)曾经到访过，则(x,y)的宽度是9（可以选择大于8并且小于min_n初始值的任何数），从而保证曾经到访过的方格一定宽于未曾到访的方格，以使得find_min不会选中曾经到访过的方格。move方法没有任何回溯，只是简单地向最窄的方向一步步走下去：

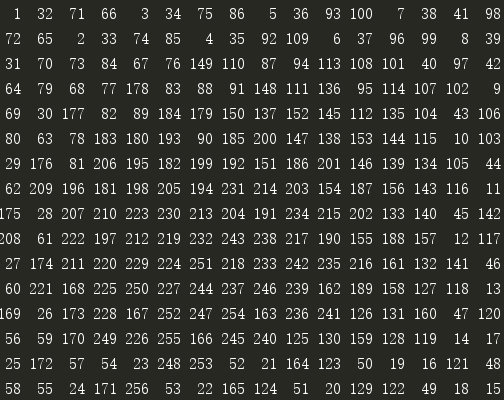
　　改成8×8或16×16的大棋盘后，KnightTourGreedy也可以快速得出结果：

　　对于一些更大的棋盘，KnightTourGreedy运行时可能会出现“RecursionError: maximum recursion depth exceeded in comparison”，这是由于递归深度超过了Python的默认限制。解决这一问题有两种方法，一种是通过sys.setrecursionlimit()修改递归的默认深度，另一种是将递归改成循环。

　　

---

　　 作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”