Fancy的照片 && luoguP1387 最大正方形

Fancy的照片

这道题在洛谷上有原题，但是洛谷上爆搜是可以过的，在模拟赛中最高得90。

P1387 最大正方形

模拟赛中的这道题目正解是一个\(n^2\)的\(DP\)，状态设\(f[i][j]\)表示以\((i,j)\)这个点为右下角的最大正方形。

如果当前点合法

\[f[i][j]=\min(f[i-1][j],f[i-1][j-1],f[i][j-1])+1\]

如果不合法

\[f[i][j]=0\]

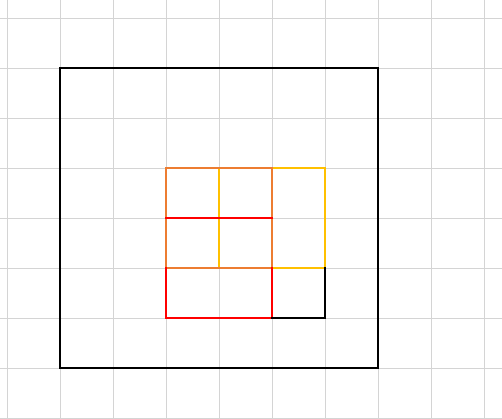
看图理解一下

如果\(f[i][j]\)从\(f[i-1][j]\)转移过来，它必须满足\(f[i-1][j-1]\)和\(f[i][j-1]\)都大于等于\(f[i-1][j]\)，才能满足正方形合法，综上所述，就是\(\min(f[i-1][j],f[i-1][j-1],f[i][j-1])\)，再加上当前的\(1\).

如果\(f[i-1][j]\)是\(2\)黄色部分要想扩展为\(3\)需满足橙色部分\(f[i-1][j-1]\)和红色部分\(f[i-1][j]\)都大于等于\(2\)，才能满足正方形这个条件。

#include
#include
using namespace std;
const int N=3e3+100;
int f[N][N];
bool mark[N][N];
int n,m;
int main()
{
    scanf("%d%d",&n,&m);
    for (int i=1;i<=m;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        mark[x][y]=1;
    }
    for (int i=1;i<=n;i++)
    for (int j=1;j<=n;j++)
    if (!mark[i][j]) f[i][j]=min(f[i-1][j-1],min(f[i-1][j],f[i][j-1]))+1;
    else f[i][j]=0;
    int ans=0;
    for (int i=1;i<=n;i++)
    for (int j=1;j<=n;j++)
    ans=max(ans,f[i][j]);
    printf("%d\n",ans);
    return 0;
}