最近重读《集体智慧编程》,这本当年出版的介绍推荐系统的书,在当时看来很引领潮流,放眼现在已经成了各互联网公司必备的技术。
这次边阅读边尝试将书中的一些Python语言例子用C#来实现,利于自己理解,代码贴在文中方便各位园友学习。
由于本文可能涉及到的与原书版权问题,请第三方不要以任何形式转载,谢谢合作。
第八部分 核方法与SVM
这一部分继续介绍一种分类器,以线性分类器为起点,逐渐引入和方法,最后到一种高阶分类器-SVM。
本文中所使用的例子是婚介数据,示例数据分为两个文件,简单的数据只有年龄及是否匹配,而复杂的数据还包括是否吸烟,是否要孩子,兴趣爱好等。
可以从这里下载这两个文件,agesonly.csv与matchmaker.csv
这两个文件的最后一列都表示是否匹配,0表示不匹配,1表示匹配。
和之前大部分文章所做的第一步一样,我们首先要加载数据。
新建名为AdvancedClassify的类,在其中实现加载方法LoadMatch,同时还有一个表示一行数据的内部类MatchRow。
public List LoadMatch(string file, bool allnum = false)
{
var rows = new List();
var fs = File.OpenRead(file);
var sr = new StreamReader(fs);
while (!sr.EndOfStream)
{
var line = sr.ReadLine();
if (string.IsNullOrEmpty(line)) continue;
rows.Add(new MatchRow(line.Split(','), allnum));
}
return rows;
}
public class MatchRow
{
public readonly string[] Data;
public readonly double[] NumData;
public readonly int Match;
public MatchRow(string[] row, bool allnum = false)
{
if (allnum)
{
NumData = new double[row.Length - 1];
for (int i = 0; i < row.Length - 1; i++)
NumData[i] = double.Parse(row[i]);
}
else
{
Data = new string[row.Length - 1];
for (int i = 0; i < row.Length - 1; i++)
Data[i] = row[i];
}
Match = int.Parse(row.Last());
}
public MatchRow(double[] row)
{
NumData = row.Take(row.Length - 1).ToArray();
Match = (int)row.Last();
}
} 数据加载得到的结果就是一个MatchRow对象的列表。我们来测试下这个LoadMatch方法。从本文开始使用xUnit.net单元测试来测试方法,取代之前在控制台程序Main函数里测试的方法。
在本系列文章结束后将把所有示例代码上传的Github,那时也会把之前几篇文章中的测试方法以单元测试的方式来重构。
public class AdvancedClassifyTest
{
private readonly ITestOutputHelper _output;
public AdvancedClassifyTest(ITestOutputHelper output)
{
_output = output;
}
private void TestOutput(object obj)
{
_output.WriteLine(obj.ToString());
}
}单元测试的方法都在上面这个类中,我们通过ITestOutputHelper来将结果输出到测试工具的Output窗口(楼主使用Resharper来运行xUnit单元测试)。下面是测试数据加载的TestLoad方法:
[Fact]
public void TestLoad()
{
var advancedClassify = new AdvancedClassify();
var agesOnly = advancedClassify.LoadMatch(@"TestData\agesonly.csv", true);
_output.WriteLine(JsonConvert.SerializeObject(agesOnly));
var matchmaker = advancedClassify.LoadMatch(@"TestData\matchmaker.csv");
_output.WriteLine(JsonConvert.SerializeObject(matchmaker));
}在上一篇文章中,我们介绍过使用MatplotlibCS生成坐标图,这一部分我们利用之前的成果,把agesonly.csv所包含的数据进行可视化。我们把男方和女方的年龄分别作为X轴和Y轴的值。
生成函数图像的方法为PlotageMatches,这里借用了上节实现的Draw方法,我们也将其原封不动的复制到当前类中:
public void PlotageMatches(List rows)
{
var xdm = rows.Where(r => r.Match == 1).Select(r => r.NumData[0]).ToList();
var ydm = rows.Where(r => r.Match == 1).Select(r => r.NumData[1]).ToList();
var xdn = rows.Where(r => r.Match == 0).Select(r => r.NumData[0]).ToList();
var ydn = rows.Where(r => r.Match == 0).Select(r => r.NumData[1]).ToList();
var axes = new Axes(1, "", "")
{
Title = "Age Distribution",
ShowLegend = false
};
for (int i = 0; i < xdm.Count; i++)
axes.PlotItems.Add(new Point2D("go", xdm[i], ydm[i]) { Marker = Marker.Point });
for (int i = 0; i < xdn.Count; i++)
axes.PlotItems.Add(new Point2D("ro", xdn[i], ydn[i]) { Marker = Marker.Plus });
Draw(new List { axes });
}
public void Draw(List plots)
{
// 由于我们在外部启动Python服务,这两个参数传空字符串就可以了
var matplotlibCs = new MatplotlibCS.MatplotlibCS("", "");
var figure = new Figure(1, 1)
{
FileName = $"/mnt/e/Temp/result{DateTime.Now:ddHHmmss}.png",
OnlySaveImage = true,
DPI = 150,
Subplots = plots
};
var t = matplotlibCs.BuildFigure(figure);
t.Wait();
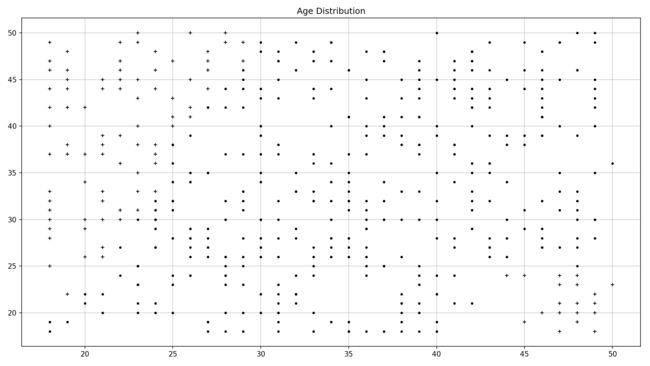
} 对于不匹配的情况使用“圆点”来表示,而匹配的情况使用“加号”来表示。
接着写在测试类里面写一个测试方法来生成图像
[Fact]
public void TestPlot()
{
var advancedClassify = new AdvancedClassify();
var agesOnly = advancedClassify.LoadMatch(@"TestData\agesonly.csv", true);
advancedClassify.PlotageMatches(agesOnly);
}生成的分布图如下:
建立这样一个分布图对于选择分类方法是有帮助的。从图中看,上篇文章介绍的决策树对于这个问题的不是特别合适,因为产生的决策树不易于解释。而且当条件增加时,决策树将变的更加复杂。
线性分类器
下面由最简单的线性分类器开始,线性分类器的原理是寻找每个分类中所有数据的平均值,并构造一个代表该分类的中心位置点。通过比较带分类数据与哪个中心位置点更近来进行分类。
首先实现计算分类的均值点的函数。本例中有两个分类0和1,分表表示不匹配和匹配。
在AdvancedClassify中加入LinearTrain方法:
public Dictionary LinearTrain(List rows)
{
var averages = new Dictionary();
var counts = new Dictionary();
foreach (var row in rows)
{
//得到该坐标点所属分类
var cl = row.Match;
if (!averages.ContainsKey(cl))
averages.Add(cl, new double[row.NumData.Length]);
if (!counts.ContainsKey(cl))
counts.Add(cl, 0);
//将该坐标点加入averages中
for (int i = 0; i < row.NumData.Length; i++)
{
averages[cl][i] += row.NumData[i];
}
//记录每个分类中有多少坐标点
counts[cl] += 1;
}
// 将总和除以计数值以求得平均值
foreach (var kvp in averages)
{
var cl = kvp.Key;
var avg = kvp.Value;
for (var i = 0; i < avg.Length; i++)
{
avg[i] /= counts[cl];
}
}
return averages;
} 可以运行下面的测试得到线性分类的均值:
[Fact]
public void TestLinearTrain()
{
var advancedClassify = new AdvancedClassify();
var agesOnly = advancedClassify.LoadMatch(@"TestData\agesonly.csv", true);
var avgs = advancedClassify.LinearTrain(agesOnly);
_output.WriteLine(JsonConvert.SerializeObject(avgs));
}输出如下:
{"1":[35.480417754569189,33.015665796344649],"0":[26.914529914529915,35.888888888888886]}
这表示分类1的中心点是(35.48,33.02),分类0的中心点是(26.91,35.89)。在进行分类时,只需要判断待分类点更接近那个点即可。
这里将使用一种不同于之前介绍的欧几里德距离的方法来判断待分类点距离那个分类中心点更近,即向量点积。
向量点积的计算很简单,即分别将第一个向量与第二个向量对应的值相乘,然后将乘机相加。表示为方法如下:
public double DotProduct(double[] v1, double[] v2)
{
return v1.Select((v, i) => v * v2[i]).Sum();
}而向量点积的另一种计算方法就是使用向量长度的乘积再乘以两向量夹角的余弦。结合两种计算方法可以方便的求出两个向量的余弦。
而向量点积有个重要特点,当夹角余弦为负值时,两个向量夹角度数大于90度,反之两个向量的夹角大于90度。
本例种我们不需要求出余弦具体值,只需要知道余弦的正负即可。由于向量长度的乘积一定为正,所以可知向量点积的符合与余弦的符号一定相同。所以我们只需要求出向量点积的正负即可。
我们按如下方法定义两个向量,将相匹配分类的均值点M到不匹配分类的均值点N作为一个向量,待分类点X到M与N的中点作为另一个向量。当X距离M更近时,两个向量的夹角将小于90度,反之大于90度。结合之前所说判断向量夹角的方法可以很容易的计算出待分类点距离那个分类的中心点更近。
用公式来表示上面的过程(两分类均值的中心点为\((M+N)/2\))
\[class=sign((X-(M+N)/2)\cdot(M-N))\]
其中,sign表示符合函数,将公式展开后:
\[class=sign(X\cdot M-X\cdot N+(M\cdot M-N\cdot N)/2)\]
用将其转为代码实现为
public int DpClassify(double[] point, Dictionary avgs)
{
var b = (DotProduct(avgs[1], avgs[1]) - DotProduct(avgs[0], avgs[0])) / 2;
var y = DotProduct(point, avgs[0]) - DotProduct(point, avgs[1]) + b;
if (y > 0) return 0;
return 1;
} 然后就可以尝试进行线性分类了:
[Fact]
public void TestDpClassify()
{
var advancedClassify = new AdvancedClassify();
var agesOnly = advancedClassify.LoadMatch(@"TestData\agesonly.csv", true);
var avgs = advancedClassify.LinearTrain(agesOnly);
var classify = advancedClassify.DpClassify(new double[] { 30, 30 }, avgs);
_output.WriteLine(classify.ToString());
classify = advancedClassify.DpClassify(new double[] { 30, 25 }, avgs);
_output.WriteLine(classify.ToString());
classify = advancedClassify.DpClassify(new double[] { 25, 40 }, avgs);
_output.WriteLine(classify.ToString());
classify = advancedClassify.DpClassify(new double[] { 48, 20 }, avgs);
_output.WriteLine(classify.ToString());
}线性分类器的一个明显缺点就是待分类数据要有一条明显的直线分界。如果找不到这样一条直线,或有多条直线,则使用线性分类器很难有正确的结果。
分类特征
不同与决策树,本文介绍的分类方法不能直接处理分类数据,我们需要先将其转为数值类型。
对于“是否”问题的处理最简单,将其转为1或0,对于数据缺失的情况,可以直接按否处理:
public int YesNo(string v)
{
if (v == "yes") return 1;
if (v == "no") return -1;
return 0;
}对于兴趣列表,采用一种简单粗暴的方法,即范围两人共同兴趣的数量。虽然这会导致一定的偏差,比如滑板与滑雪有一定联系,但采用这里的方法它们仍然会按0处理。复杂一点可以将兴趣分为大类,并对这些大类进行比较给出一个0-1之间的关联程度值。
public int MatchCount(string interest1, string interest2)
{
var l1 = interest1.Split(':');
var l2 = interest2.Split(':');
return l1.Intersect(l2).Count();
}对于距离的确定,可以使用一些地图网站提供的API将地址转为经纬度并计算距离,但这里我们不做处理。返回0。
public int MilesDistance(string a1, string a2)
{
return 0;
}构造新的数据集
有了上面的分类数据处理方法,我们可以将那份复杂的婚配数据处理为数值类型。
public List LoadNumerical()
{
var oldrows = LoadMatch(@"TestData\matchmaker.csv");
var newrows = new List();
foreach (var row in oldrows)
{
var d = row.Data;
var data = new[]
{
double.Parse(d[0]),
YesNo(d[1]),
YesNo(d[2]),
double.Parse(d[5]),
YesNo(d[6]),
YesNo(d[7]),
MatchCount(d[3], d[8]),
MilesDistance(d[4], d[9]),
row.Match
};
newrows.Add(new MatchRow(data));
}
return newrows;
} 验证一下处理后的数值数据是否正确:
[Fact]
public void TestLoadNumerical()
{
var advancedClassify = new AdvancedClassify();
var numericalset = advancedClassify.LoadNumerical();
var dataRow = numericalset[0].Data;
_output.WriteLine(JsonConvert.SerializeObject(dataRow));
}和之前很多篇文章相同,我们需要对数值数据进行缩放以使其据有可比性:
public Tuple, Func> ScaleData(List rows)
{
var low = ArrayList.Repeat(999999999.0, rows[0].NumData.Length).Cast().ToList();
var high = ArrayList.Repeat(-999999999.0, rows[0].NumData.Length).Cast().ToList();
// 寻找最大值和最小值
foreach (var row in rows)
{
var d = row.NumData;
for (int i = 0; i < row.NumData.Length; i++)
{
if (d[i] < low[i]) low[i] = d[i];
if (d[i] > high[i]) high[i] = d[i];
}
}
//对数据进行缩放处理的函数
// 注意:原书印刷代码有问题,配书代码是正确的,还要自己做一下“除0”的处理
Func scaleInput = d =>
low.Select((l, i) =>
{
if (high[i] == low[i]) return 0;
return (d[i] - low[i]) / (high[i] - low[i]);
}).ToArray();
//对所有数据进行缩放处理
var newrows = rows.Select(r =>
{
var newRow = scaleInput(r.NumData).ToList();
newRow.Add(r.Match);
return new MatchRow(newRow.ToArray());
}).ToList();
return Tuple.Create(newrows, scaleInput);
} 我们将数值数据缩放到0-1之间,并返回缩放函数。在后面分类时,我们需要首先对待分类数据进行缩放然后才能将其传入分类器。
现在可以用更大规模的数据测试线性分类器了。
[Fact]
public void TestScaledLinearTrain()
{
var advancedClassify = new AdvancedClassify();
var numericalset = advancedClassify.LoadNumerical();
var result = advancedClassify.ScaleData(numericalset);
var scaledSet = result.Item1;
var scalef = result.Item2;
var avgs = advancedClassify.LinearTrain(scaledSet);
_output.WriteLine(JsonConvert.SerializeObject(numericalset[0].NumData));
_output.WriteLine(numericalset[0].Match.ToString());
_output.WriteLine(advancedClassify.DpClassify(scalef(numericalset[0].NumData), avgs).ToString());
_output.WriteLine(numericalset[11].Match.ToString());
_output.WriteLine(advancedClassify.DpClassify(scalef(numericalset[11].NumData), avgs).ToString());
}通过结果可以看到线性分类器很难满足多维数据处理的要求。下面将介绍一种新的分类方法。
核方法
如我们有这样两类数据,其中一个分类的数据分布于X(-2,2)Y(-2,2)之间的坐标轴中心位置,而另一个分类数据分布于这之外的坐标空间。一个分类的数据将另一个分类的数据环绕其中,所以这个明显不可能使用线性分类来处理。但如果我们将这些数据进行变换,将每个点进行平方处理。则一个分类的数据将位于X(0,4)Y(0,4)这个坐标范围,而另一个分类数据将落于X(4,+∞)Y(4,+∞)这个范围。很明显,这样处理后可以使用一条直线将两种分类划分开来。
而进行分类时只需要将待分类数据进行平方并传入分类器进行判断即可。
当然实际例子中可能要进行多次变换才能将数据转为线性分类可处理的数据。
实际编程实现中不会使用上面介绍的那种映射方法,使用这种特定的变化方法很难将多维的数据转为高维空间中有明确分界线的数据。一种更好的方法被称为核技法,其适用于任何使用点积运算算法的问题。
核技法的目的就是将一个线性分类器转换成非线性分类器。
核技法可以采用多种不同的映射方法,一种备受推崇,也是本文要介绍的方法称为径向基函数(radial-basis function简称RBF)。
核方法将使用映射方法代替点积函数,新函数返回高维度坐标空间中的点积结果。(个人感觉原书要表达的意思是,映射方法可以像点积函数那样利用正负对传入值进行分类而不是真正返回点积结果)所以我们可以将这个映射函数套用于之前得到的公式。
\[class=sign(X\cdot M-X\cdot N+(M\cdot M-N\cdot N)/2)\]
将其中的点积函数换成我们的映射方法,即径向基函数。
另一个问题,这个公式需要分类数据的均值点,而目前均值点是在原始坐标空间计算得到,这个均值点无法直接使用,而又无法计算新坐标空间中的均值点,因为不会计算每一个点在新坐标空间的位置。但,先对一组向量求均值,然后再计算均值与向量A的点积与先计算一组向量中每一个向量与向量A的点积然后计算均值是等价的。
有了上面的这些积累,下面就可以开始代码实现了
首先实现径向基函数
public double Rbf(double[] v1, double[] v2, int gamma = 20)
{
var dv = v1.Select((v, i) => v - v2[i]).ToArray();
var l = VecLength(dv);
return Math.Pow(Math.E, -gamma * l);
}
public double VecLength(double[] v)
{
return v.Sum(p => p * p);
}径向基函数的签名与向量点积计算方法类似。但其是非线性的,可以将数据映射到更为复杂的空间,而且通过调整参数gamma还可以针对特定数据集得到最佳线性分离。
然后就是利用径向基函数进行分类的方法:
public int NlClassify(double[] point, List rows, double offset, int gamma = 10)
{
double sum0 = 0;
double sum1 = 0;
var count0 = 0;
var count1 = 0;
foreach (var row in rows)
{
if (row.Match == 0)
{
sum0 += Rbf(point, row.NumData, gamma);
++count0;
}
else
{
sum1 += Rbf(point, row.NumData, gamma);
++count1;
}
}
var y = sum0 / count0 - sum1 / count1 + offset;
if (y > 0) return 0;
return 1;
}
public double GetOffset(List rows, int gamma = 10)
{
var l0 = new List();
var l1 = new List();
foreach (var row in rows)
{
if (row.Match == 0)
l0.Add(row.NumData);
else
l1.Add(row.NumData);
}
var sum0 = (from v2 in l0 from v1 in l0 select Rbf(v1, v2, gamma)).Sum();
var sum1 = (from v2 in l1 from v1 in l1 select Rbf(v1, v2, gamma)).Sum();
return sum1 / (l1.Count * l1.Count) - sum0 / (l0.Count * l0.Count);
} 其中,GetOffset就是计算公式中\(M\cdot M-N\cdot N\)这一部分。由于每次分类过程,这个值都是固定的,我们可以事先将其计算存储。
下面尝试下使用核方法预测的效果,首先使用只有年龄的数据:
[Fact]
public void TestNlClassify()
{
var advancedClassify = new AdvancedClassify();
var agesOnly = advancedClassify.LoadMatch(@"TestData\agesonly.csv", true);
var offset = advancedClassify.GetOffset(agesOnly);
TestOutput(advancedClassify.NlClassify(new[] { 30.0, 30 }, agesOnly, offset));
TestOutput(advancedClassify.NlClassify(new[] { 30.0, 25 }, agesOnly, offset));
TestOutput(advancedClassify.NlClassify(new[] { 25.0, 40 }, agesOnly, offset));
TestOutput(advancedClassify.NlClassify(new[] { 48.0, 20 }, agesOnly, offset));
}从结果可以看出,核方法比起普通线性分类好了不少。接着尝试下复杂数据的处理:
[Fact]
public void TestNlClassifyMore()
{
var advancedClassify = new AdvancedClassify();
var numericalset = advancedClassify.LoadNumerical();
var result = advancedClassify.ScaleData(numericalset);
var scaledSet = result.Item1;
var scalef = result.Item2;
var ssoffset = advancedClassify.GetOffset(scaledSet);
TestOutput(numericalset[0].Match);
TestOutput(advancedClassify.NlClassify(scalef(numericalset[0].NumData), scaledSet, ssoffset));
TestOutput(numericalset[1].Match);
TestOutput(advancedClassify.NlClassify(scalef(numericalset[1].NumData), scaledSet, ssoffset));
TestOutput(numericalset[2].Match);
TestOutput(advancedClassify.NlClassify(scalef(numericalset[2].NumData), scaledSet, ssoffset));
var newrow = new[] { 28, -1, -1, 26, -1, 1, 2, 0.8 };//男士不想要小孩,而女士想要
TestOutput(advancedClassify.NlClassify(scalef(newrow), scaledSet, ssoffset));
newrow = new[] { 28, -1, 1, 26, -1, 1, 2, 0.8 };//双方都想要小孩
TestOutput(advancedClassify.NlClassify(scalef(newrow), scaledSet, ssoffset));
}支持向量机
支持向量机的主要思想就是找到一条尽可能远离所有分类的线,这条线被称为最大间隔超平面(maximum-margin hyperplane)。
选择这个分界线的方法是,寻找两条分别经过各分类相应坐标点的平行线,并使其与分界线的距离尽可能的远。只有位于间隔区域边缘的坐标点才是确定分界线所必须的,抹去其余所有数据也不影响分界线的位置。这条分界线附近的点就称为支持向量。寻找支持向量,并利用支持向量来寻找分界线的算法便是支持向量机(SVM)。
这样对于待分类的点,只要判断其位于分类线的哪一侧就可以知道所属的分类。
支持向量机所使用的也是点积的结果,因此也可以利用核技法将其用于非线性分类。
从零开始实现一个支持向量机非常复杂,有一个很好的开源支持向量机可以用于我们的例子 - LibSVM。LibSVM库可以对SVM模型进行训练,给出预测及利用数据集对预测结果进行测试,同时其也提供了类似径向基函数这样的核方法的支持。
这里使用LibSVM库的一个C#包装 - LibSVMsharp来进行分类测试。
首先给出一个简单的例子,其可以让你快速了解LibSVMsharp的使用:
[Fact]
public void LibsvmFirstLook()
{
var prob = new SVMProblem();
prob.Add(new[] { new SVMNode(1, 1), new SVMNode(2, 0), new SVMNode(3, 1) }, 1);
prob.Add(new[] { new SVMNode(1, -1), new SVMNode(2, 0), new SVMNode(3, -1) }, -1);
var param = new SVMParameter();
param.Kernel = SVMKernelType.LINEAR;
param.C = 10;
var m = prob.Train(param);
TestOutput(m.Predict(new []{new SVMNode(1,1), new SVMNode(2, 1), new SVMNode(3, 1) }));
m.SaveModel("trainModel");
var ml = SVM.LoadModel("trainModel");
TestOutput(ml.Predict(new[] { new SVMNode(1, 1), new SVMNode(2, 1), new SVMNode(3, 1) }));
}所有LibSVM的使用代码都直接实现在测试方法中
运行测试方法,需要手动拷贝libsvm.dll到Debug目录下
代码中首先构造训练数据,指定分类方法,对模型进行训练,然后进行预测。训练模型也可以进行保存,并在未来加载用于分类。
有了LibSVMsharp的使用介绍,可以对婚配数据进行预测。
[Fact]
public void TestLibsvmClassify()
{
var advancedClassify = new AdvancedClassify();
var numericalset = advancedClassify.LoadNumerical();
var result = advancedClassify.ScaleData(numericalset);
var scaledSet = result.Item1;
var scalef = result.Item2;
var prob = new SVMProblem();
foreach (var matchRow in scaledSet)
{
prob.Add(matchRow.NumData.Select((v,i)=>new SVMNode(i+1,v)).ToArray(),matchRow.Match);
}
var param = new SVMParameter() {Kernel = SVMKernelType.RBF};
var m = prob.Train(param);
m.SaveModel("trainModel");
Func makeInput = ma => scalef(ma).Select((v, i) => new SVMNode(i + 1, v)).ToArray();
var newrow = new[] { 28, -1, -1, 26, -1, 1, 2, 0.8 };//男士不想要小孩,而女士想要
TestOutput(m.Predict(makeInput(newrow)));
newrow = new[] { 28, -1, 1, 26, -1, 1, 2, 0.8 };//双方都想要小孩
TestOutput(m.Predict(makeInput(newrow)));
} 代码依然很容易理解,先将婚配数据转为LibSVM所需要的输入,执行分类方法为径向基函数,进行训练然后测试分类。
为了达到更好的预测结果,可以使用前文的CrossValidate方法进行交叉验证,然后调整LibSVM参数再次进行交叉验证,直到得到满意的结果。
优缺点
支持向量机是非常强大的分类方法,只要提供合适的参数,支持向量机的分类效果至少达到甚至超过之前介绍的其他分类器。另外分类速度快也是支持向量机的一个优势,因为其只需要判断坐标位于分界线的哪一侧。
支持向量机的缺点也在于参数,对于每种不同的训练数据,我们都需要确定参数。这就需要反复用交叉验证去确定合适的参数。所以支持向量机更适于有大量训练数据的场景。另外支持向量机和神经网络都是黑盒技术 - 我们很难去解释其给出结果的具体细节。