TensorFlow 系列案例(4)及Pytorch 学习(3)实现K-Means聚类算法
TensorFlow 系列案例(4)及Pytorch 实现K-Means聚类算法
本文参考网络资料,将通过三种方式实现K-Means聚类算法。(代码均来源于网络,在此致谢互联网人工智能大牛们的奉献)
- 传统的机器学习K-Means聚类算法
- TensorFlow实现K-Means聚类算法
- Pytorch实现K-Means聚类算法
K-MEANS算法是输入聚类个数k,以及包含 n个数据对象的数据库,输出满足方差最小标准k个聚类的一种算法。k-means 算法接受输入量 k ;然后将n个数据对象划分为 k个聚类以便使得所获得的聚类满足:同一聚类中的对象相似度较高;而不同聚类中的对象相似度较小。
基本步骤
(1) 从 n个数据对象任意选择 k 个对象作为初始聚类中心;
(2) 根据每个聚类对象的均值(中心对象),计算每个对象与这些中心对象的距离;并根据最小距离重新对相应对象进行划分;
(3) 重新计算每个(有变化)聚类的均值(中心对象);
(4) 计算标准测度函数,当满足一定条件,如函数收敛时,则算法终止;如果条件不满足则回到步骤(2)。
K值按WCSS计算方法进行选取。
传统的机器学习K-Means聚类算法:
# -*- coding: utf-8 -*-
import numpy as np
from numpy.linalg import cholesky
import matplotlib.pyplot as plt
sampleNo = 1000 #数据数量
mu =3
# 二维正态分布
mu = np.array([[1, 5]])
Sigma = np.array([[1, 0.5], [1.5, 3]])
R = cholesky(Sigma)
srcdata= np.dot(np.random.randn(sampleNo, 2), R) + mu
X=srcdata
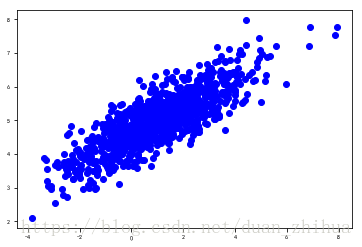
plt.plot(srcdata[:,0],srcdata[:,1],'bo')
from sklearn.cluster import KMeans
# Fitting K-Means to the dataset
kmeans = KMeans(n_clusters =2, init = 'k-means++', random_state = 42)
y_kmeans = kmeans.fit_predict(X)
L1=[]
L2=[]
for i in range(len(y_kmeans)):
L1.append(srcdata[i][0])
L2.append(srcdata[i][1])
#用来正常显示中文标签
plt.rc('font', family='SimHei', size=6)
#用来正常显示负号
plt.rcParams['axes.unicode_minus']=False
p1 = plt.subplot(221)
plt.title(u"Kmeans聚类 n=2")
plt.scatter(L1,L2,c=y_kmeans,marker="s")
plt.sca(p1)
###################################
# 聚类 类蔟数=3
kmeans = KMeans(n_clusters =3, init = 'k-means++', random_state = 42)
y_kmeans = kmeans.fit_predict(X)
p2 = plt.subplot(222)
plt.title("Kmeans n=3")
plt.scatter(L1,L2,c=y_kmeans,marker="s")
plt.sca(p2)
###################################
# 聚类 类蔟数=4
kmeans = KMeans(n_clusters =4, init = 'k-means++', random_state = 42)
y_kmeans = kmeans.fit_predict(X)
p3 = plt.subplot(223)
plt.title("Kmeans n=4")
plt.scatter(L1,L2,c=y_kmeans,marker="+")
plt.sca(p3)
###################################
# 聚类 类蔟数=5
kmeans = KMeans(n_clusters =5, init = 'k-means++', random_state = 42)
y_kmeans = kmeans.fit_predict(X)
p4 = plt.subplot(224)
plt.title("Kmeans n=5")
plt.scatter(L1,L2,c=y_kmeans,marker="+")
plt.sca(p4)
#保存图片本地
plt.savefig('k_kmeans.png', dpi=300)
plt.show()
运行结果如下:
TensorFlow实现K-Means聚类算法
# -*- coding: utf-8 -*-
import numpy as np
from numpy.linalg import cholesky
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import tensorflow as tf
from random import choice, shuffle
from numpy import array
############Sachin Joglekar的基于tensorflow写的一个kmeans模板###############
def KMeansCluster(vectors, noofclusters):
"""
K-Means Clustering using TensorFlow.
`vertors`应该是一个n*k的二维的NumPy的数组,其中n代表着K维向量的数目
'noofclusters' 代表了待分的集群的数目,是一个整型值
"""
noofclusters = int(noofclusters)
assert noofclusters < len(vectors)
#找出每个向量的维度
dim = len(vectors[0])
#辅助随机地从可得的向量中选取中心点
vector_indices = list(range(len(vectors)))
shuffle(vector_indices)
#计算图
#我们创建了一个默认的计算流的图用于整个算法中,这样就保证了当函数被多次调用时,默认的图并不会被从上一次调用时留下的未使用的OPS或者Variables挤满
graph = tf.Graph()
with graph.as_default():
#计算的会话
sess = tf.Session()
##构建基本的计算的元素
##首先我们需要保证每个中心点都会存在一个Variable矩阵
##从现有的点集合中抽取出一部分作为默认的中心点
centroids = [tf.Variable((vectors[vector_indices[i]]))
for i in range(noofclusters)]
##创建一个placeholder用于存放各个中心点可能的分类的情况
centroid_value = tf.placeholder("float64", [dim])
cent_assigns = []
for centroid in centroids:
cent_assigns.append(tf.assign(centroid, centroid_value))
##对于每个独立向量的分属的类别设置为默认值0
assignments = [tf.Variable(0) for i in range(len(vectors))]
##这些节点在后续的操作中会被分配到合适的值
assignment_value = tf.placeholder("int32")
cluster_assigns = []
for assignment in assignments:
cluster_assigns.append(tf.assign(assignment,
assignment_value))
##下面创建用于计算平均值的操作节点
#输入的placeholder
mean_input = tf.placeholder("float", [None, dim])
#节点/OP接受输入,并且计算0维度的平均值,譬如输入的向量列表
mean_op = tf.reduce_mean(mean_input, 0)
##用于计算欧几里得距离的节点
v1 = tf.placeholder("float", [dim])
v2 = tf.placeholder("float", [dim])
euclid_dist = tf.sqrt(tf.reduce_sum(tf.pow(tf.subtract(
v1, v2), 2)))
##这个OP会决定应该将向量归属到哪个节点
##基于向量到中心点的欧几里得距离
#Placeholder for input
centroid_distances = tf.placeholder("float", [noofclusters])
cluster_assignment = tf.argmin(centroid_distances, 0)
##初始化所有的状态值
##这会帮助初始化图中定义的所有Variables。Variable-initializer应该定
##义在所有的Variables被构造之后,这样所有的Variables才会被纳入初始化
init_op = tf.global_variables_initializer()
#初始化所有的变量
sess.run(init_op)
##集群遍历
#接下来在K-Means聚类迭代中使用最大期望算法。为了简单起见,只让它执行固
#定的次数,而不设置一个终止条件
noofiterations = 20
for iteration_n in range(noofiterations):
##期望步骤
##基于上次迭代后算出的中心点的未知
##the _expected_ centroid assignments.
#首先遍历所有的向量
for vector_n in range(len(vectors)):
vect = vectors[vector_n]
#计算给定向量与分配的中心节点之间的欧几里得距离
distances = [sess.run(euclid_dist, feed_dict={
v1: vect, v2: sess.run(centroid)})
for centroid in centroids]
#下面可以使用集群分配操作,将上述的距离当做输入
assignment = sess.run(cluster_assignment, feed_dict = {
centroid_distances: distances})
#接下来为每个向量分配合适的值
sess.run(cluster_assigns[vector_n], feed_dict={
assignment_value: assignment})
##最大化的步骤
#基于上述的期望步骤,计算每个新的中心点的距离从而使集群内的平方和最小
for cluster_n in range(noofclusters):
#收集所有分配给该集群的向量
assigned_vects = [vectors[i] for i in range(len(vectors))
if sess.run(assignments[i]) == cluster_n]
#计算新的集群中心点
new_location = sess.run(mean_op, feed_dict={
mean_input: array(assigned_vects)})
#为每个向量分配合适的中心点
sess.run(cent_assigns[cluster_n], feed_dict={
centroid_value: new_location})
#返回中心节点和分组
centroids = sess.run(centroids)
assignments = sess.run(assignments)
return centroids, assignments
############生成测试数据###############
sampleNo = 1000;#数据数量
mu =3
# 二维正态分布
mu = np.array([[1, 5]])
Sigma = np.array([[1, 0.5], [1.5, 3]])
R = cholesky(Sigma)
srcdata= np.dot(np.random.randn(sampleNo, 2), R) + mu
plt.plot(srcdata[:,0],srcdata[:,1],'bo')
############kmeans算法计算###############
k=4
center,result=KMeansCluster(srcdata,k)
print( center )
############利用seaborn画图###############
res={"x":[],"y":[],"kmeans_res":[]}
for i in range(len(result)):
res["x"].append(srcdata[i][0])
res["y"].append(srcdata[i][1])
res["kmeans_res"].append(result[i])
pd_res=pd.DataFrame(res)
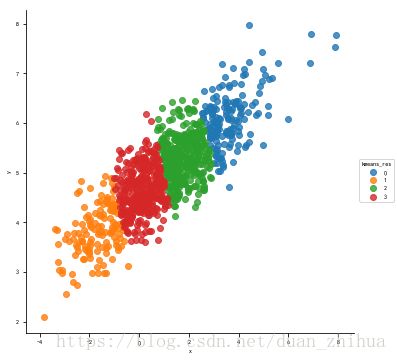
sns.lmplot("x","y",data=pd_res,fit_reg=False,size=5,hue="kmeans_res")
plt.show()运行结果如下:
Pytorch实现K-Means聚类算法:
from kmeans import lloyd
import numpy as np
import matplotlib.pyplot as plt
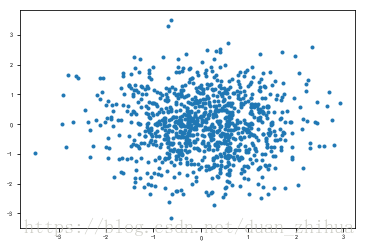
X = np.random.randn(1000, 2)
fig, ax = plt.subplots()
ax.plot(X[:, 0], X[:, 1], '.')
fig.show()
choice_cluster, initial_state = lloyd(X,4)
fig, ax = plt.subplots()
for i in range(4):
indices = np.where(choice_cluster==i)[0]
selected = X[indices]
ax.plot(selected[:, 0], selected[:, 1], '.', label=str(i))
fig.show()
import torch
import numpy as np
from pairwise import pairwise_distance
def forgy(X, n_clusters):
_len = len(X)
indices = np.random.choice(_len, n_clusters)
initial_state = X[indices]
return initial_state
def lloyd(X, n_clusters, device=0, tol=1e-4):
#3000 *2
X = torch.from_numpy(X).float()
#4*2 中心点位置
initial_state = forgy(X, n_clusters)
while True:
#3000*4 计算距离
dis = pairwise_distance(X, initial_state)
#3000 选择的分类
choice_cluster = torch.argmin(dis, dim=1)
# 4*2
initial_state_pre = initial_state.clone()
for index in range(n_clusters):
#1950
selected = torch.nonzero(choice_cluster==index).squeeze()
# 1950*2
selected = torch.index_select(X, 0, selected)
#4*2
initial_state[index] = selected.mean(dim=0)
center_shift = torch.sum(torch.sqrt(torch.sum((initial_state - initial_state_pre) ** 2, dim=1)))
if center_shift ** 2 < tol:
break
return choice_cluster.cpu().numpy(), initial_state.cpu().numpy()r'''
calculation of pairwise distance, and return condensed result, i.e. we omit the diagonal and duplicate entries and store everything in a one-dimensional array
'''
import torch
def pairwise_distance(data1, data2=None, device=-1):
r'''
using broadcast mechanism to calculate pairwise ecludian distance of data
the input data is N*M matrix, where M is the dimension
we first expand the N*M matrix into N*1*M matrix A and 1*N*M matrix B
then a simple elementwise operation of A and B will handle the pairwise operation of points represented by data
'''
if data2 is None:
data2 = data1
if device!=-1:
data1, data2 = data1.cuda(device), data2.cuda(device)
#N*1*M 3000*1*2
A = data1.unsqueeze(dim=1)
#1*N*M 1*4*2
B = data2.unsqueeze(dim=0)
#3000*4*2
dis = (A-B)**2.0
#return N*N matrix for pairwise distance
#3000*4
dis = dis.sum(dim=-1).squeeze()
return dis
def group_pairwise(X, groups, device=0, fun=lambda r,c: pairwise_distance(r, c).cpu()):
group_dict = {}
for group_index_r, group_r in enumerate(groups):
for group_index_c, group_c in enumerate(groups):
R, C = X[group_r], X[group_c]
if device!=-1:
R = R.cuda(device)
C = C.cuda(device)
group_dict[(group_index_r, group_index_c)] = fun(R, C)
return group_dict
运行结果为:
全面化人工智能可能意味着人类的终结……机器可以自行启动,并且自动对自身进行重新设计,速率也会越来越快。受到漫长的生物进化历程的限制,人类无法与之竞争,终将被取代。
---史蒂芬·霍金