hdu6185 Covering （递推+矩阵快速幂）

Problem Description
Bob’s school has a big playground, boys and girls always play games here after school.

To protect boys and girls from getting hurt when playing happily on the playground, rich boy Bob decided to cover the playground using his carpets.

Meanwhile, Bob is a mean boy, so he acquired that his carpets can not overlap one cell twice or more.

He has infinite carpets with sizes of 1×2 and 2×1, and the size of the playground is 4×n.

Can you tell Bob the total number of schemes where the carpets can cover the playground completely without overlapping?

Input
There are no more than 5000 test cases.

Each test case only contains one positive integer n in a line.

1≤n≤10^18

Output
For each test cases, output the answer mod 1000000007 in a line.

Sample Input
1
2

Sample Output
1
5

大致题意：让你用1*2规格的地毯去铺4*n规格的地面，告诉你n，问有多少种不同的方案使得地面恰好被铺满且地毯不重叠。答案对1000000007取模

思路：考虑全部铺满时，前2列的放法。有如下5种情况：

假设f（n）表示列数为n时的方案数，那么这五种情况合法的方案数相加即f（n）。这里n大于2.
第一种的方案数即f（n-1），第二种的方案数即f（n-2）。
第三种：接下来有两种方案可以选择，一是用一块毛毯去填补第二列的空缺部分，那么此时接下来填补的方案数为f（n-2），二是用两块毛毯去填补，这样的话第三列又会形成一个新的空缺，如下图所示：

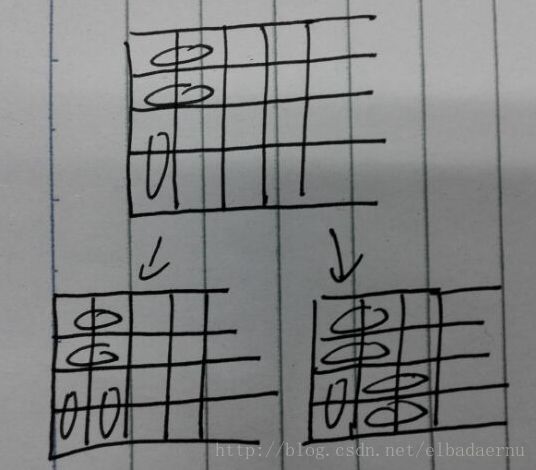
所以我们又可以像之前那样去填补，所以第三种的方案数为f（n-2）+f（n-3）+f（n-4）+……+f（0）,f（0）=1
第四种：情况与第三种类似，方案数与其相同。
第五种：开始的选择也是两种，一是选择一块毯子去填，这样接下来填补的方案数为f（n-2），或者选择两块去填，然后，为了使它铺满，我们还得用两块毛毯去铺上下两个空缺的地方，这时的空缺形成了之前的情况，如下图所示：

以此类推，所以第五种的方案数为f（n-2）+f（n-4）+f（n-6）+……+f（1）或者f（0）（偶数0，奇数1）

所以总的方案数
f（n）=f（n-1）+f（n-2）+2*（f（n-2）+f（n-3）+……+f（0））+f（n-2）+f（n-4）+f（n-6）+……+f（1）或者f（0）
然后将n=n-2代入上式，然后用f（n）减去f（n-2），
化简得f（n）=f（n-1）+5*f（n-2）+f（n-3）-f（n-4）。
因为n很大，所以接下来用矩阵快速幂搞搞就可以了。

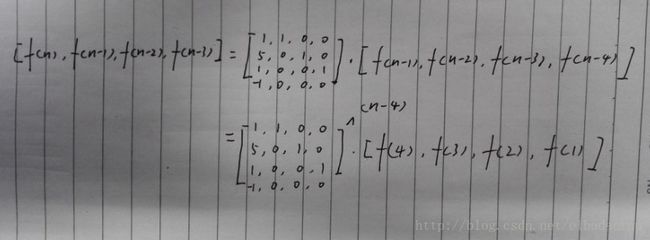
代码如下

#include  
#include 
#include 
using namespace std; 
#define LL long long 
const int mod=1000000007; 
struct matrix
{
    LL x[4][4];
};
matrix mutimatrix(matrix a,matrix b)
{
    matrix temp; 
    memset(temp.x,0,sizeof(temp.x));    
    for(int i=0;i<4;i++)
    for(int j=0;j<4;j++)
    for(int k=0;k<4;k++)
    {
        temp.x[i][j]+=a.x[i][k]*b.x[k][j];
        temp.x[i][j]%=mod;
    }
    return temp;
}

matrix k_powmatrix(matrix a,LL n)//矩阵快速幂
{
    matrix temp;
    memset(temp.x,0,sizeof(temp.x));
    for(int i=0;i<4;i++)
    temp.x[i][i]=1;

    while(n)
    {
        if(n&1)
        temp=mutimatrix(temp,a);

        a=mutimatrix(a,a);
        n>>=1;
    }
    return temp;
} 


int main()
{

        LL n;

        while(scanf("%lld",&n)!=EOF)
        {
            //前面四个手算下
            if(n==1)
            {
                printf("1\n");
                continue;
            }
            if(n==2)
            {
                printf("5\n");
                continue;
            }
            if(n==3)
            {
                printf("11\n");
                continue;
            }
            if(n==4)
            {
                printf("36\n");
                continue;
            }

        matrix st;
        memset(st.x,0,sizeof(st.x));
        st.x[0][0]=1;
        st.x[1][0]=5;
        st.x[2][0]=1;
        st.x[3][0]=-1;

        st.x[0][1]=1;
        st.x[1][2]=1;
        st.x[2][3]=1;

        matrix init;//初始矩阵
        memset(init.x,0,sizeof(init.x));

        init.x[0][0]=36;
        init.x[0][1]=11;
        init.x[0][2]=5;
        init.x[0][3]=1;


        st=k_powmatrix(st,n-4);//经过n-4次相乘
        st=mutimatrix(init,st);//然后再乘上初始矩阵

        printf("%lld\n",(st.x[0][0]+mod)%mod);
    }
    return 0; 
}