NOIP2017普及组复赛题解

T1 score 题面：

（不想看的跳过吧）

无疑，这是一道可以媲美A+B Problem的大水题，刚开始看到，以为要用浮点数操作之类的，但是题目给出A,B,C全部小于等于100并且都为10的倍数，所以就使这道题变成了彻彻底底的水题。
题意大概如此：给出三个均为10的倍数并且小于等于100的整数A,B,C，以整数形式输出 A∗20%+B∗30%+C∗50% 。
显然
A∗20%=A∗20/100=A/5
B∗30%=B∗30/100=A∗3/10
C∗50%=C∗50/100=C/2
为什么要这样算呢，因为这样能够避免浮点数运算，粗心出错的概率也就小了很多，下面是代码：

#include 

int a, b, c, ans;

int main()
{
    scanf("%d%d%d", &a, &b, &c);
    ans = a / 5 + b * 3 / 10 + c / 2;
    printf("%d\n", ans);
    return 0;
}

(真的需要给这题题解吗？)

T2 librarian 题面

（不想看的跳过吧）


刚开始看，以为是什么有套路的题目，实际上就是一道模拟。
题意：有一个n个元素的字典，元素都是整数，给出q个询问，每个询问有一个十进制下长度为a的整数b，求字典的n个元素中在十进制下，后a位与b相等的元素中，字典序最小的一个，如果没有则输出-1。（其实不如看题面）
思路：模拟
首先读入n个整数，没有必要以字符串形式读入，当然字符串也可以做。
那么对于每一个整数b（a其实是没有用的），我们设一个p[i]，p[i]=1表示a[i]不以b结尾，即不符合要求；其余的p[i]=0就是符合条件的。那么剩下的工作就是把n个元素中满足p[i]=0的元素取一个最小值，问题就转化为了如何求p数组。具体步骤：将b与其它几个a[i]末尾对齐，此时b的最后一位为b mod 10，a[i]的最后一位为a[i] mod 10，显然在(b mod 10)和(a[i] mod 10)不相等时，p[i]=1，然后就把b和a[i]同时/10，移动到下一位比较，直到b为0为止。比较过程如下：
（题目数据中23的比较）

（题目数据中123的比较）

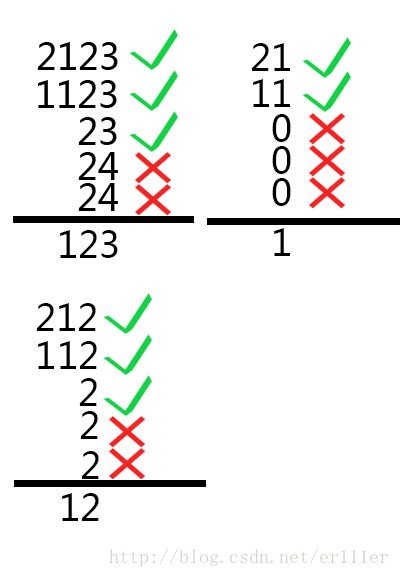
时间复杂度为O(nq)，题目数据显然不会超时。
代码：

#include 
#include 

const int N = 1007, INF = 666666666; //个人习惯，别在意哈
int n, q, a, b, ans = INF;
int num[N], t[N], p[N];

int main()
{
    scanf("%d%d", &n, &q);
    for (int i = 1; i <= n; i++)
        scanf("%d", &num[i]); //以整数形式读入数据
    while (q--)
    {
        memset(p, 0, sizeof(p)); //初始化
        memcpy(t, num, sizeof(num)); //将原数组拷贝一份，以免破坏原数组
        ans = INF; //将答案赋初值
        scanf("%d%d", &a, &b); //虽然a没用，但也要读入
        while (b != 0) //循环往复直至b == 0
        {
            for (int i = 1; i <= n; i++) //把每个t[i]和b比较
            {
                if (t[i] % 10 != b % 10) //最后一位不等
                    p[i] = 1; //标记为1
                t[i] /= 10; //移动至下一位
            }
            b /= 10; //移动至下一位
        }
        for (int i = 1; i <= n; i++) //寻找满足p[i] == 0的num[i]
            if (!p[i] && num[i] < ans) //p[i] == 0且能更新答案
                ans = num[i]; //更新答案
        if (ans == INF) //答案没有改变，说明没有这么一个元素满足p[i] == 0
            printf("-1\n");
        else
            printf("%d\n", ans);
    }
    return 0;
}

T3 chess 题面

（一定要认真看！！！）



刚看到的时候觉得好烦，本来是没打算做的，后来为了水点分，打了dfs+剪枝，竟然90，丢的10分是低级错误，事实证明还是要敢做敢想。
题意：在一个m*m的矩阵上，求(1,1)到(m,m)的最低花费，移动的规则如下：
1.棋盘上有n个格子有颜色，颜色为红色或黄色，其余皆为无色。
2.每次移动仅能向上下左右四个相邻的格子移动。
3.(x1,y1)移动到(x2,y2)的必要条件是(x1,y1)和(x2,y2)都有色。
3.如果(x1,y1)和(x2,y2)都有色并且颜色相同，则花费为0。
4.如果(x1,y1)和(x2,y2)都有色并且颜色不同，则花费为1。
5.如果(x2,y2)为无色的，则可以花费2使得(x2,y2)变为一个红黄中任意一种颜色然后走过去，在走上原本就有颜色的格子前，不能再次使一个格子变色。
6.第3条相当于每次站立的点必须有色。
思路：dfs+剪枝 OR bfs+最短路
dfs+剪枝：
我们可以设一个 f[x][y] 为(1,1)到达(x,y)的最小花费，这样就可以开始搜索。搜索函数dfs(x, y, tag)表示搜到(x,y)，tag=0即不能变色，tag=1表示可以变色，具体过程就是把(x,y)向四个方向扩展出(dx,dy)，那么可以分出四种情况：
1.(dx,dy)越界，此时直接return。
2.(dx,dy)无色，那么此时就将(dx,dy)变为与(x,y)同色（以保证花费最小），然后递归到dfs(dx, dy, 0)，记得返回时将(dx,dy)回溯为无色。
3.(dx,dy)有色且与(x,y)颜色相同，此时直接走至dfs(dx, dy, 1)。
4.(dx,dy)有色且与(x,y)颜色不同，此时直接走至dfs(dx, dy, 1)。
但是这样有一个问题，那就是可以能出现两个点一直互相跳，陷入死循环的局面。考虑情况2，如果 f[x][y]+2>=f[dx][dy] ，那么 f[dx][dy] 也不可能更新出更优的f，也就是当 f[x][y]+2<f[dx][dy] 时，才有必要从(x,y)走至(dx,dy)，其它的几种情况也是同理，这样就实现了一个剪枝。
代码：

#include 
#include 

const int N = 107, D[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}}; //可扩展的节点
int a[N][N], f[N][N]; //a为颜色数组，-1表示无色，0和1表示其他颜色
int n, m, x, y, c;

inline int hf(int x, int y) { return (x <= n && x > 0 && y <= n && y > 0); } //判断坐标是否合法(hf)

void dfs(int x, int y, int tag) //搜索
{
    for (int i = 0; i < 4; i++)
    {
        int dx = x + D[i][0], dy = y + D[i][1]; //扩展出节点(dx,dy)
        if (hf(dx, dy)) //跳过不合法的节点
        {
            if (a[dx][dy] == -1) //(dx,dy)无色的情况
            {
                if (f[x][y] + 2 < f[dx][dy]/*如上文所说剪枝*/ && tag/*可以变色*/)
                {
                    f[dx][dy] = f[x][y] + 2; //更新f数组
                    a[dx][dy] = a[x][y]; //变色
                    dfs(dx, dy, 0); //tag改为0
                    a[dx][dy] = -1; //回溯
                }
            }
            else if (a[dx][dy] == a[x][y]) //有色且颜色相同
            {
                if (f[x][y] < f[dx][dy]/*上文所述剪枝*/)
                {
                    f[dx][dy] = f[x][y]; //更新
                    dfs(dx, dy, 1); //走至(dx,dy)
                }
            }
            else if (a[dx][dy] != a[x][y]) //有色且颜色不同
            {
                if (f[x][y] + 1 < f[dx][dy]/*上文所述剪枝*/)
                {
                    f[dx][dy] = f[x][y] + 1; //更新
                    dfs(dx, dy, 1); //走至(dx,dy)
                }
            }
        }
    }
}

int main()
{
    memset(a, -1, sizeof(a));
    memset(f, 0x3f, sizeof(f)); //赋为无穷大

    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; i++)
    {
        scanf("%d%d%d", &x, &y, &c);
        a[x][y] = c;
    }
    f[1][1] = 0; //(1,1)为出发点，距离自然为0
    dfs(1, 1, 1);
    if (f[n][n] == 0x3f3f3f3f) //无法到达
        printf("-1\n");
    else
        printf("%d\n", f[n][n]);
    return 0;
}

bfs+最短路：
看到矩阵AND最小，很自然地想到最短路，思路与SPFA差不多，只是dis要多设一维表示颜色，其余做法同SPFA，代码：

#include 
#include 

struct point { int x, y, col, tag; };
const int N = 107, D[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int a[N][N], dis[N][N][2], vis[N][N][2][2];
point que[N * N * 10]; //多乘一点保险
int n, m, x, y, c, head = 1, tail= 0;

inline int hf(int x, int y) { return (x <= n && x > 0 && y <= n && y > 0); } //合法
inline int min(int a, int b) { return a < b ? a : b; } //自定义min函数，比STL不知道快多少

int main()
{
    memset(dis, 0x3f, sizeof(dis)); //初始化无穷大
    memset(vis, 0, sizeof(vis));
    memset(a, -1, sizeof(a));

    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; i++)
    {
        scanf("%d%d%d", &x, &y, &c);
        a[x][y] = c;
    }
    que[++tail] = (point){1, 1, a[1][1], 1};
    dis[1][1][a[1][1]] = 0, vis[1][1][a[1][1]][1] = 1;
    while (head <= tail)
    {
        point tmp = que[head++];
        vis[tmp.x][tmp.y][tmp.col][tmp.tag] = 0; //标记出队
        for (int i = 0; i < 4; i++) //扩展节点
        {
            int dx = tmp.x + D[i][0], dy = tmp.y + D[i][1];
            if (hf(dx, dy))
            {
                if (a[dx][dy] == -1)
                {
                    if (dis[tmp.x][tmp.y][tmp.col] + 2 < dis[dx][dy][tmp.col] && tmp.tag)
                    {
                        dis[dx][dy][tmp.col] = dis[tmp.x][tmp.y][tmp.col] + 2;
                        if (!vis[dx][dy][tmp.col][0])
                        {
                            que[++tail] = (point){dx, dy, tmp.col, 0};
                            vis[dx][dy][tmp.col][0] = 1;
                        }
                    }
                }
                else if (a[dx][dy] == tmp.col)
                {
                    if (dis[tmp.x][tmp.y][tmp.col] < dis[dx][dy][tmp.col])
                    {
                        dis[dx][dy][tmp.col] = dis[tmp.x][tmp.y][tmp.col];
                        if (!vis[dx][dy][tmp.col][1])
                        {
                            que[++tail] = (point){dx, dy, tmp.col, 1};
                            vis[dx][dy][tmp.col][1] = 1;
                        }
                    }
                }
                else if (a[dx][dy] != tmp.col)
                {
                    if (dis[tmp.x][tmp.y][tmp.col] + 1 < dis[dx][dy][a[dx][dy]])
                    {
                        dis[dx][dy][a[dx][dy]] = dis[tmp.x][tmp.y][tmp.col] + 1;
                        if (!vis[dx][dy][a[dx][dy]][1])
                        {
                            que[++tail] = (point){dx, dy, a[dx][dy], 1};
                            vis[dx][dy][a[dx][dy]][1] = 1;
                        }
                    }
                }
            }
        }
    }
    if (dis[n][n][0] == 0x3f3f3f3f && dis[n][n][1] == 0x3f3f3f3f) //两种颜色都无法走到
        printf("-1\n");
    else
        printf("%d\n", min(dis[n][n][0], dis[n][n][1]));
    return 0;
}

T4 jump 题面

(认真，认真，认真看！！！)


不愧是T4，难度也是普及蒟蒻所不能及的。
这一题要解决的就两个问题：
1.如何求最小的g。
2.如何在d,g给定的情况下，求出能得到的最大分数。
问题1是很容易想到的，g必然是在 [0,Xn] 之间的，那么就可以二分答案求解了，重点在于问题2，如何求出最大分数呢？考虑DP，我们设 f[i] 为跳到i时的最大分数，那么最大分数即为 max(f[i]:1≤i≤n) ，根据定义可得转移方程为：
mx=d+g
mi=min(d−g,1)
f[i]=max(f[j]:1≤j<i且x[j]+mx≥x[i]且x[j]+mi≤x[i])+a[i]
mi是最小跳跃距离，mx是最大跳跃距离。朴素的DP是 O(n2lgx) 的，必然超时。优化方法是用单调队列（学习单调队列点这里 单调队列详解），还是像老套路一样，求出 f[i] 就将其入队，当x[que[head]] + mx < x[i]时出队。当初没有打单调队列，是因为我没能解决 x[j]+mi≤x[i] 这个条件，其实我们可以设一个now，对于所有now

#include 
#include 

const int N = 500007;
int dis[N], num[N], f[N], que[N];
int n, d, k, l, r, ans = 0;

int check(int val)
{
    memset(f, -127, sizeof(f)); //因为分数有负数，所以赋为负无穷大
    int head = 1, tail = 0, mi = val < d ? d - val : 1, mx = d + val, ret = 0, fir = -1;
    que[++tail] = 0, f[0] = 0; //初始化
    for (int i = 1; i <= n; i++)
    {
        if (dis[i] < mi) continue; //< mi的点肯定跳不到
        if (dis[i] >= mi && fir == -1) //第一个点初始化
            fir = i;
        if (dis[i] - dis[i - 1] > mx) break; //相邻两个已经 > mx了，那么后面的肯定也都不行
        while (dis[i] - dis[fir] >= mi && fir < i) //当fir满足x[fir]+mi<=x[i]时入队
        {
            while (head <= tail && f[fir] > f[que[tail]]) tail--; //入队
            que[++tail] = fir++; //入队
        }
        while (head <= tail && dis[que[head]] + mx < dis[i]) head++; //不满足x[que[head]] + mx >= x[i]的都出队
        if (head > tail) //对于点i，没有一个点可以跳到
            f[i] = -0x7f7f7f7f; //设为赋无穷大
        else
            f[i] = f[que[head]] + num[i]; //转移
        if (f[i] > ret) //更新最大分数
            ret = f[i];
    }
    return ret >= k; //能够拿到>= k的分数
}

int main()
{
    scanf("%d%d%d", &n, &d, &k);
    for (int i = 1; i <= n; i++)
        scanf("%d%d", dis + i, num + i);
    l = 0, r = dis[n];
    while (l <= r) //二分答案
    {
        int mid = (l + r) >> 1;
        if (check(mid)) //答案可行
            r = mid - 1, ans = mid/*记录答案*/;
        else
            l = mid + 1;
    }
    if (check(ans)) //保险判断一下
        printf("%d\n", ans);
    else
        printf("-1\n");
    return 0;
}

这次普及组的T1意外的水，T4却意外的难，而且出乎意料的没有数学题或者思维题，只要是提高-水平的选手一般都能想到3、4题正解，大爱CCF。