排序(上)——为什么插入排序比冒泡排序更受欢迎?
本文是学习算法的笔记,《数据结构与算法之美》,极客时间的课程
排序对于每个程序员来说,可能都不会陌生。平常的项目中,也经常遇到排序。按时间复杂度,分成三类,分三节来说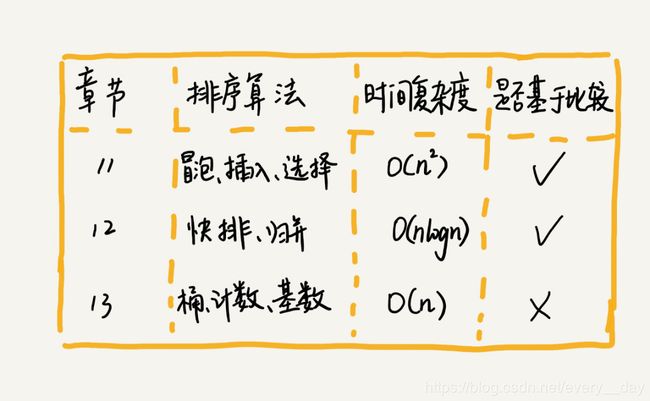
这里,先抛出一个问题。插入排序和冒泡排序的时间复杂度都是O(n2),可实际开发中,为什么我们更倾向于使用插入排序算法呢?
评价一个排序算法,
从效率角度说,要考虑各种时间复杂度;数据量小时,时间复复杂度的系数、常数也要考虑;元素比较和交换的次数。
从内存消耗角度说,要考虑算法的空间复杂度。空间复杂度是o(1)的排序算法,叫原地排序算法(Sorted in place)。今天说的三种算法都是原地排序算法。
从算法稳定性来说,排序算法又分为稳定性算法和非稳定性算法。稳定性,指相等元素,在排序后,原来的先后顺序不改变。
稳定性算法相对于不稳定性算法,有什么特别的用么,反正是等值,谁先谁后,不都一个样子么?实际业务中,可能会按多个属性排序。比如这么一个场景:有一批订单,按日期降序排列,如果日期一样的,按订单金额降序。
这个需要很好理解,实现起来,可能就没那么容易,按日期排好了,再把日期一样的按订单金额排一次。这个就不好实现,先把日期一样的分别取出来排下,再对应放回去,很麻烦。
有了稳定性排序算法,就很容易实现。第一步,先按订单金额降序排列,第二步,再把第一步得到的结果,按日期降序重新排列一次,就可以实现需求了。为什么自己琢磨一下吧。
接着,我们详细说下这三种排序算法,我会分别给出代码实现(java),简要说下复杂度,还有算法的评价等等。
冒泡排序算法
基本的逻辑是,取第一个元素与后一个比较,如果大于后者,就与后者互换位置,不大于,就保持位置不变。再拿第二个元素与后者比较,如果大于后者,就与后者互换位置。一轮比较之后,最大的元素就移动到末尾。相当于最大的就冒出来了。再进行第二轮,第三轮,直到排序完毕。

代码实现,我们会做一些优化,如果是n个元素,第一轮比较(n-1)次,第二轮,比较(n-2)次就可以了。直到剩余两个元素,比较1次,排序操作就结束了。再进一步优化,如果,在某一轮操作中,只有比较操作,而没有数据移动操作,那说明已经完全有序,不需要再进行下一轮了,直接结束即可。
/**
* 冒泡排序
*
* @param a
* @return
*/
public int[] bubbleSort(int[] a) {
int n = a.length;
if (n <= 1) {
return a;
}
for (int i = 1; i < n; i++) {
boolean flag = false; // 开关,当某次内层循环,没有数据交换时,已排好顺序,直接跳出循环。
for (int j = 0; j < n - i; j++) {
if (a[j] > a[j + 1]) {
int temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
flag = true;
}
}
if (!flag) {
break;
}
}
return a;
}
分析冒泡排序的时间复杂度,最好情况时间复杂度是O(n)。最好的情况本身就是有序的,比较了一轮,一次冒泡,不需要移动元素,排序完成。
最坏情况时间复杂度是O(n2)。最坏情况刚好是反序的(结合本例,就是倒序),要进行(n-1)轮的比较,每轮比较都要进行(n-1)次的位置移动。
平均情况时间复杂度也是为O(n2)。这个用加权平均算概率有点复杂。理论是,n个元素,排列方式就在有 n! 种,每种情况下,比较多少轮,每次多少数据移动都不一样。有一点是确定的,上限是O(n2),下限是o(n)。
这里,我们引入一个简化的比较方式。

有序度:满足 a[m] > a[n],且 m > n 的一对数,
逆序度:满足 a[m] > a[n],且 m < n 的一对数,
满序度:有序度的最大值(或逆序度的最大值)。潢序度 = 有序度 + 逆序度
对于冒泡排序,冒泡一次,有序度至少增加一,当达到满度时,排序就结束。在 n! 种排列中,有序度最小值是0,最大值是(n-1)*n/2,平均值就是(n-1)*n/4。有序度可以评价冒泡排序的比较操作,移动元素的操作肯定比比较的操作少,那冒泡排序的平均情况时间复杂度是 (n-1)*n/4 至 最坏情况时间复杂度之间的值,不考虑系数,低阶,得O(n2)。
冒泡排序的空间复杂度是O(1),数据移动需要一个临时变量,属于常量级别。
冒泡排序是稳定性算法,从实现的代码,可以推知,当相同元素比对时,不会进行数据移动。
插入排序算法
基本逻辑是,把元素分为已排序的和未排序的。每次从未排序的元素取出第一个,与已排序的元素从尾到头逐一比较,找到插入点,将之后的元素都往后移一位,腾出位置给该元素。

/**
* 插入排序
*
* @param a
* @return
*/
public int[] insertSort(int[] a) {
int n = a.length;
if (n <= 1) {
return a;
}
for (int i = 1; i < n; i++) {
int temp = a[i];
int j = i - 1;
for (; j >= 0; j--) {
if (a[j] > temp) {
a[j + 1] = a[j]; // 比temp 大的已排序数据后移一位
} else {
break;
}
}
a[j + 1] = temp; // 空出来的位置,把temp放进去
}
return a;
}
插入排序,最好情况时间复杂度,如果已经是一个有序数组了,就不需要移动数据。只要查找到插入位置即可,每次只需要一次比较就可以找到插入位置,所以,这种情况下,最好情况时间复杂度为O(n)。
如果数组是倒序的,每次插入都相当于在数组的第一个位置插入数据,有大量移动数据的操作,所以,最坏情况时间复杂度是O(n2)。
数组中插入一个数据平均时间复杂度是O(n),要进行n次操作,所以,平均情况时间复杂度是O(n2)。
空间复杂度是O(1)。也是一种稳定性算法。
选择排序算法
基本逻辑是:把所有数据分为已排序区间和未排序区间。每次从未排序区间中,选出最小值,之后将该值与未排序区间第一个元素互换位置,此时已排序区间元素个数多了一个,未排序区间内的元素少了一个。如此循环直到未排序区间没有元素为止。
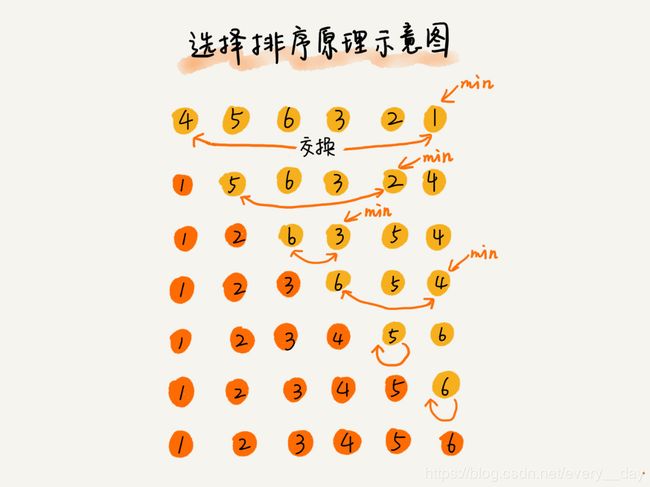
/**
* 选择排序
*
* @param a
* @return
*/
public int[] selectionSort(int[] a) {
int n = a.length;
if (n <= 1) {
return a;
}
for (int i =1; i < n; i++) {
int j = i-1;
int min = a[j]; // 最小的数值
int index = j; // 最小值对应的下标
for (; j < n-1 ; j++) {
if (min > a[j+1]) {
min = a[j+1];
index = j+1;
}
}
//最小值a[index]与放未排序的首位a[i-1]互换位置
if (index != i-1) {
int temp = a[i-1];
a[i-1] = a [index];
a [index] = temp;
}
}
return a;
}
选择排序算法,最好情况时间复杂度与最坏情况时间复杂度,都是O(n2),空间复杂度是O(1),它是不稳定的算法。相同元素,排序后,相对位置可能发生改变。
比较下三种算法的效率,我在测试类中,分别取800,8000,80000个元素进行排序,结果如下
@Test
public void testParseResult() {
Random rand = new Random();
int length = 800;
int[] a = new int[length];
int[] b = new int[length];
int[] c = new int[length];
for (int i = 0; i < length; i++) {
a[i] = rand.nextInt(100);
b[i] = a[i];
c[i] = a[i];
// System.out.print(" " + b[i]);
// if (i % 50 == 49) {
// System.out.println();
// }
}
long one = System.currentTimeMillis();
insertSort(a);
long two = System.currentTimeMillis();
bubbleSort(b);
long three = System.currentTimeMillis();
selectionSort(c);
long four = System.currentTimeMillis();
System.out.println(" ");
System.out.println("数组长度值为:" + length);
System.out.println("插入排序用时(单位毫秒):" + (two - one));
System.out.println("冒泡排序用时(单位毫秒):" + (three - two));
System.out.println("选择排序用时(单位毫秒):" + (four - three));
// System.out.println();
// for (int i = 0; i < length; i++) {
// System.out.print(" " + a[i]);
// if (i % 10 == 9) {
// System.out.println();
// }
// }
}
数组长度值为:800
插入排序用时(单位毫秒):3
冒泡排序用时(单位毫秒):5
选择排序用时(单位毫秒):2
数组长度值为:8000
插入排序用时(单位毫秒):56
冒泡排序用时(单位毫秒):148
选择排序用时(单位毫秒):24
数组长度值为:80000
插入排序用时(单位毫秒):2385
冒泡排序用时(单位毫秒):11067
选择排序用时(单位毫秒):1163
现在说说文章开头的问题,同为稳定性排序算法,时间复杂度也一样,插入排序的效率比冒泡排序要好,尤其是数据量大的时候,差距更明显。为什么?
冒泡排序移动数据的操作更多,只要是小于后一个元素,就移动一次。所以它的效率低。看测试结果,八万的时候,就是数量级的差距了。