【coding】动态规划

在 bilibili 看到一个博主讲的比较好的动态规划内容，自己对应整理了一下学习笔记，以便巩固学习

题目一：Fibonacci

代码简单实现

/**
 * Creation         :       2018.11.18 17:03
 * Last Reversion   :       2018.11.18 17:08
 * Author           :       Lingyong Smile {[email protected]}
 * File Type        :       cpp
 * -----------------------------------------------------------------
 * Fibonacci
 *      Everyone knows the Fibonacci sequence. Now you need to enter an integer n.
 *      Please output the nth item of the Fibonacci sequence (starting at 0 and 0th item is 0).
 *      0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
 * -----------------------------------------------------------------
 * Crop right @ 2018 Lingyong Smile {[email protected]}
 */

#include 
using namespace std;

/**
 * 递归方式
 */ 
int FibonacciRecursive(int n) {
    if (n == 0)
        return 0;
    else if (n == 1)
        return 1;
    return FibonacciRecursive(n - 2) + FibonacciRecursive(n - 1);
}

/**
 * 非递归：动态规划
 */ 
int Fibonacci(int n) {
    if (n == 0) return 0;
    if (n == 1) return 1;
    int a = 0;
    int b = 1;
    int c;
    for (int i = 2; i <= n; i++) {
        c = a + b;
        a = b;
        b = c;
    }
    return c;
}

int main() {
    int n;
    cout << "Please input a int number:";
    while (cin >> n) {
        // Test Fibonacci function
        cout << "Fibonacci(" << n << ") is : " << Fibonacci(n) << endl;

        // Test Fibonacci Recursive function
        cout << "FibonacciRecursive(" << n << ") is : " << FibonacciRecursive(n) << endl;
        cout << "Please input a int number:";
    }
    // system("pause");
    return 0;
}

---

题目二：最多能赚几块钱？

横轴代表时间，灰色的长方条代表从某一时刻开始的任务，长方条上的数字代表完成这个任务能够赚几块钱，比如最上面的第1个任务，表示从1点开始，4点结束，完成这个任务可以获得5元钱。其中有一个限制，开始了某一任务后，只有做完这个任务才能做下一个，比如开始做了任务7，则不能做任务4、5、6、8，因为有时间冲突。现在有一个员工，如何才能赚最多的钱，最多能赚几块钱？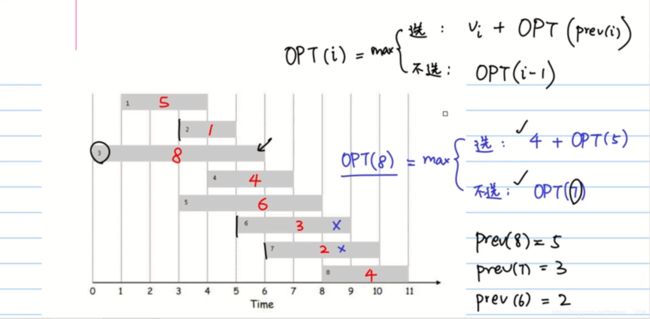

从上往下分析，得出递推公式（选不选）

其中 $OPT(i)$ 表示，当我要考虑前 $i$ 个任务时，它的最优解是什么，即最多能赚几块钱？
例如：当考虑前8个任务时 $OPT(8)$，对于任务8有两种状态，选和不选。

• 选第8个任务，首先可以赚4块钱，再加上 $OPT(5)$ ，即加上前面5个任务的最优解，最多能赚几块钱。（因为选了任务8则和任务6和7有时间冲突）
• 不选第8个任务，则就是前面7个任务的最优解 $OPT(7)$

然后选这两个状态结果最大的，作为前8个任务的最优解 $OPT(8)$ ，即得到如下递归公式：
$$OPT(8)=max\{\begin{array}{rlrl}& & 4+OPT(5)& ,选任务8\\ & & OPT(7)& ,不选任务8\end{array}$$

整理一下递推公式：
$$OPT(i)=max\{\begin{array}{rlrl}& & v_i+OPT(prev(i))& ,选任务i\\ & & OPT(i-1)& ,不选任务i\end{array}$$

其中 $v_i$ 表示第 $i$ 个任务的奖励工资，$prev(i)$ 表示如果要做第 $i$ 个任务，则它前面顶多还能做前几个。例如：$prev(8)=5$ 表示如果要做第8个任务，则前面顶多还能做前5个，即加上考虑前5个任务的最优解 $OPT(prev(8))$。

首先计算 $prev$ 数组，比如 $i=1$ 时，$prev(1)=0$ 表示如果做任务1，则前面能做的为0个，以此类推。我们最终要算的是前面8个任务的最优解，即 $OPT(8)$ ，根据递归式可以得到如上状结构，可以发现：(1)首先这是一个找最优解问题。(2)大问题的最优解依赖于子问题的最优解。(3)大问题分解成子问题，子问题间有重复子问题。 这样的问题就可以使用动态规划思想来做。从上往下分析问题，从下往上求解问题。从 $OPT(1)$ 开始分析计算并保存对应结果。
$OPT(1)=v_1=5$
$OPT(2)$ 分析：如果不选任务2，则是 $OPT(1)=5$ ；如果选任务2，则是 $OPT(prev(2))+任务2价值=0+1$ 。最后选这两个状态的最大值作为前个任务2的最优解，所以 $OPT(2)=5$。表示如果只有前面两个任务的时候，最多能挣5块钱。

$OPT(4)$ 分析：如果不选任务4，则是 $OPT(3)=8$ ；如果选任务4，则是 $OPT(prev(4))+任务4价值=OPT(1)+v_4=5+4=9$ 。最后选这两个状态的最大值作为前4个任务的最优解，所以 $OPT(4)=9$。表示如果只有前面4个任务的时候，最多能挣9块钱。

后面以此类推，直到分析完前8个任务。

代码简单实现

/**
 * Creation         :       2019.04.05 14:50
 * Last Reversion   :       2019.03.05 15:22
 * Author           :       Lingyong Smile {[email protected]}
 * File Type        :       cpp
 * -----------------------------------------------------------------
 * 最多能赚几块钱(动态规划) 结合笔记题目查看
 * -----------------------------------------------------------------
 * Crop right @ 2019 Lingyong Smile {[email protected]}
 */
#include 
#include 
#include 
#define max(a, b) (((a) > (b)) ? (a) : (b))
#define min(a, b) (((a) < (b)) ? (a) : (b))

int v[9] = {0, 5, 1, 8, 4, 6, 3, 2, 4};     // 注意这里前面多补了一个0，是为了方便和笔记对应
int prev[9] = {0, 0, 0, 0, 1, 0, 2, 3, 5};  // 这里的prev数组是自己预先算好了的

/**
 * 递归形式
 */ 
int OPTRecursive(int n) {
    if (n == 0)
        return 0;
    if (n == 1)
        return 5;
    return max(OPTRecursive(n - 1) , v[n] + OPTRecursive(prev[n]));
}

/**
 * 非递归形式：（动态规划）
 */ 
int OPT(int n) {
    if (n == 0)
        return 0;
    if (n == 1)
        return 5;
    int *OPT = (int*)malloc(sizeof(int) * (n + 1));     // 这里多开辟了一个int空间大小，是为了和公式下标对应
    OPT[0] = 0;
    OPT[1] = 5;
    for (int i = 2; i <= n; i++) {
        OPT[i] = max(OPT[i-1], v[i] + OPT[prev[i]]);
    }
    int res = OPT[n];
    free(OPT);
    return res;
}

int main() {
    int n;
    printf("Please input a int number (1~8):\n");
    while (~scanf("%d", &n) && n >= 1 && n <= 8) {
        printf("%d\n", OPT(n));
    }
    return 0;
}

---

题目三：最大和

在如下一堆数字中选出一些数字，如何让数字之和最大？
限定条件：选出的数字不能是相邻的。

从上往下分析，得出递归公式（选不选）

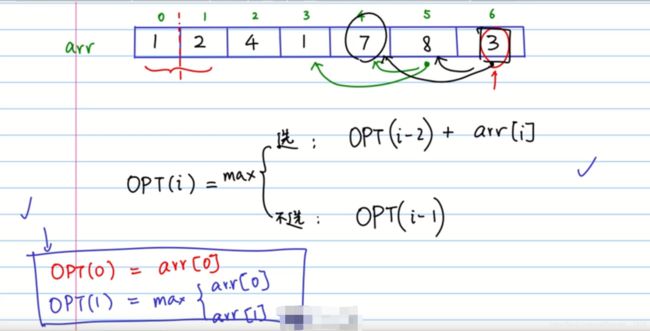
$OPT(6)$ ：表示到下标为6 这个位置的最佳方案（最优解）是什么？
从上往下开始分析：对于 $OPT(6)$ 我们有两种状态，选3，和不选3。即有如上递归式。

• 选 $arr[6]$，此时的最佳方案是 $OPT(4)+arr[6]$ 。这里不能选 $arr[5]$ ，因为 $arr[5]$ 与 $arr[6]$ 是相邻的。
• 不选 $arr[6]$，此时最佳方案是 $OPT(5)$

然后选这两个状态结果最大的，作为到下标为6这个位置的最优解 $OPT(6)$

进而，我们可以得到这样的递归方程：

$$OPT(i)=max\{\begin{array}{rlrl}& & OPT(i-2)+arr[i]& ,选arr[i]\\ & & OPT(i-1)& ,不选arr[i]\end{array}$$

分析递归出口

$$\begin{gathered} OPT(0)=arr[0] \\ OPT(1)=max(arr[0],arr[1]) \end{gathered}$$

代码简单实现

/**
 * Creation         :       2019.04.06 11:10
 * Last Reversion   :       2019.04.06 11:23
 * Author           :       Lingyong Smile {[email protected]}
 * File Type        :       cpp
 * -----------------------------------------------------------------
 * 题目描述：
 *    在如下一堆数字中选出一些数字，如何让数字之和最大？
 * 限定条件：选出的数字不能是相邻的。
 * arr[7] = {1, 2, 4, 1, 7, 8, 3}
 * -----------------------------------------------------------------
 * Crop right @ 2019 Lingyong Smile {[email protected]}
 */
#include 
#include 
#include 

#define max(a, b) (((a) > (b)) ? (a) : (b))
#define min(a, b) (((a) < (b)) ? (a) : (b))

int arr[7] = {1, 2, 4, 1, 7, 8, 3};

/**
 * 递归形式，不好存在很多重叠子问题
 */ 
int OPTRec(int n) {
    if (n == 0)
        return arr[0];
    else if (n == 1)
        return max(arr[0], arr[1]);
    else
        return max(OPTRec(n - 2) + arr[n], OPTRec(n - 1));
}

/**
 * 非递归形式：动态规划
 */ 
int OPT(int n) {
    if (n == 0)
        return arr[0];
    else if (n == 1)
        return max(arr[0], arr[1]);
    
    int *OPT = (int*)malloc(sizeof(int) * (n + 1));     // 注意这里开辟的数组大小，n为下标，从0开始
    OPT[0] = arr[0];
    OPT[1] = max(arr[0], arr[1]);
    for (int i = 2; i <= n; i++) {
        OPT[i] = max(OPT[i-2] + arr[i], OPT[i-1]);
    }
    int res = OPT[n];
    free(OPT);
    return res;
}

int main() {
    int n;
    printf("Please input a int number (0~7):\n");
    while (~scanf("%d", &n) && n >= 0 && n <= 7) {
        printf("%d\n", OPT(n));
    }
    return 0;
}

---

题目四：是否存在和为指定值

在如下一堆数字中选出一些数字求和，使其等于数字 $S$。如果存在这样的方案则返回 $true$，否则返回 $false$。

从上往下分析，得出递归公式（选不选）

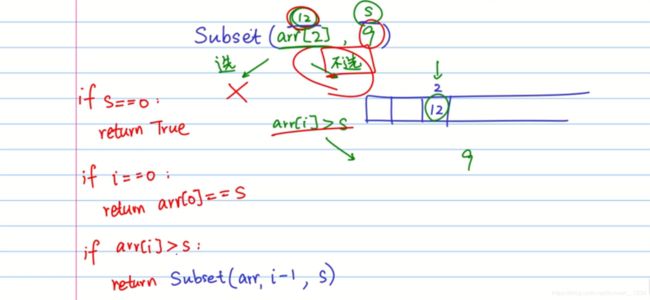
分析：我们定义 $Subset$ 表示子集，$Subset(arr[5],9)$ 表示对前面5个数字取数求和为9，应该怎么分配。从上往下分析，当 $i=5$ 时，我们有两种状态：

• 选 $arr[5]$ ，此时方案为 $Subset(arr[4],7)$ ，选了 $arr[5]$ 之后，只需要前面4个数字取数之和为7就可以。
• 不选 $arr[5]$ ，此时方案为 $Subset(arr[4],9)$ ，前面4个数字取数之和为9。

最后只要这两种方案有一个为 $true$，则满足要求，所以中间用 $or$

分析递归出口

• $S==0$ 时， 比如 $Subset(arr[2],0)$ ，表示，2后面的数字已经存方案可以使得取数求和等于 $S$ ，即这个时候已满足要求，返回 $true$
• $i==0,S!=0$ 时，即表示处理到第一个数字，只有当 $arr[i]==S$ 才会返回 $true$ ，否则返回 $false$ 。比如，当我们给的数组只有一个元素是，只有当 $arr[0]==S$ 时才为 $true$
  
• $arr[i]>S$ 时，这时候我们肯定不能选 $arr[i]$ ，即此时返回 $Subset(arr[i-1],S)$
  
  整理一下递归公式如下：
  

动态规划解法

即非递归方式，我们需要借助二维数组，保存我们的中间过程（中间的这些重叠子问题）。如下设计我们的二维数组：

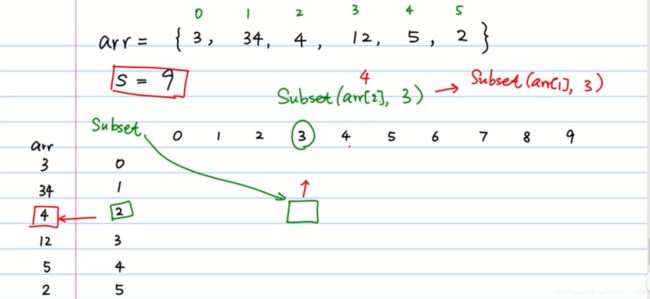
其中，最左边列是 $arr[]$ 数组，右边是设计一个二维数组，行坐标表示下标 $i$ ，纵坐标表示 $S$ ，比如图中的绿色方框表示 $Subset(arr[2],3)$ 此时，由于 $a[2]=4>S=3$ ，所以只能不选 $arr[2]$ ，即得到当前方案 $Subset(arr[1],3)$ 。明白含义之后，我们来定义我们的出口条件：

• 当 $i=0$ 时，只有 $arr[0]=S$ 时返回 $True$ ，其余都为 $False$ 。即我们写好了 $i=0$ 这一行的出口条件
• 当 $S=0$ 时，说明已经找到了取数方案，直接返回 $True$ 。即我们写好了 $S=0$ 这一列的出口条件。

然后按照从左往右的顺序，把每一行填好，最后返回最后一个结果即可。

对于 $subset[0,0]$ 我们规定为 $False$

代码简单实现

/**
 * Creation         :       2019.04.06 11:30
 * Last Reversion   :       2019.04.06 15:39:
 * Author           :       Lingyong Smile {[email protected]}
 * File Type        :       cpp
 * -----------------------------------------------------------------
 * 题目描述：
 *    在如下一堆数字中选出一些数字求和，能够等于数字n。如果存在这样的方案则
 * 返回true，否则返回false。
 * int arr[] = {3, 34, 4, 12, 5, 2};
 * 测试用例：
 输入：
9
10
11
12
13
 输出：
1
1
1
1
0
 * -----------------------------------------------------------------
 * Crop right @ 2019 Lingyong Smile {[email protected]}
 */
#include 
#include 
#include 
#define N_SIZE 100
#define M_SIZE 100

int arr[] = {3, 34, 4, 12, 5, 2};
int subset[N_SIZE][M_SIZE];

/**
 * 递归形式
 */ 
int RecSubset(int arr[], int i, int S) {
    if (i == 0)                 // 这里的两个出口和调换了一下顺序（与笔记想笔记），因为比如当数组只有一个元素arr[] = {4}, S = 5，此时因该返回False才对。
        return (arr[0] == S);
    else if(S == 0)
        return 1;
    else 
        return RecSubset(arr, i-1, S-arr[i]) || RecSubset(arr, i-1, S);
}

/**
 * 非递归形式：动态规划
 */ 
int DPSubset(int arr[], int len, int S) {
    for (int i = 0; i < len; i++) {     // 将S == 0 列都初始化为True
        subset[i][0] = 1;
    }
    for (int s = 0; s <= S; s++) {      // 将 i == 0 行，除了arr[0]列初始化为True，其余都初始化为False
        subset[0][s] = 0;
    }
    subset[0][arr[0]] = 1;

    for (int i = 1; i < len; i++) {
        for (int s = 1; s <= S; s++) {
            if (arr[i] > s)
                subset[i][s] = subset[i-1][s];
            else {
                subset[i][s] = (subset[i-1][s-arr[i]] || subset[i-1][s]);
            }
        }
    }
    return subset[len-1][S];
}

int main() {
    if (RecSubset(arr, 5, 13))
        printf("True\n");
    else
        printf("False\n");
    if (DPSubset(arr, 6, 13))
        printf("True\n");
    else
        printf("False\n");
    return 0;
}

Todo

• 01背包
• 完全背包
• 多重背包

Reference

• https://www.bilibili.com/video/av16544031/?spm_id_from=333.788.videocard.0