- 三点or多点的变换矩阵求解opencv & eigen
合工大机器人实验室
C++矩阵opencv线性代数
《Estimating3-DRigidBodyTransformations:AComparisonofFourMajorAlgorithms》,它使用SVD方法计算T和t。只要算出变换矩阵,就可以算出A坐标系的一个点P在坐标系B里的对应点坐标,即R为3x3的转换矩阵,t为3x1的位移变换向量,这里点坐标均为3x1的列向量(非齐次形式,齐次形式下为4x1列向量,多出的一个元素值补1而已)。理论上只
- Study Plan For Algorithms - Part29
五月的风与火
StudyPlanForAlgorithmspython算法数据结构
1.在排序数组中查找数字统计一个数字在排序数组中出现的次数。方法一:defsearch(nums,target):returnhelper(nums,target)-helper(nums,target-1)defhelper(nums,target):i=0j=len(nums)-1whileitargetor(lowerandnums[mid]>=target):right=mid-1else
- 翻译 Compaction wiki
i_need_job
网址:https://github.com/facebook/rocksdb/wiki/Compaction有道CompactionCompactionalgorithmsconstraintheLSMtreeshape.Theydeterminewhichsortedrunscanbemergedbyitandwhichsortedrunsneedtobeaccessedforareadoper
- Python深度学习-环境
cunzai1985
tensorflowpython深度学习人工智能anaconda
Python深度学习-环境(PythonDeepLearning-Environment)Inthischapter,wewilllearnabouttheenvironmentsetupforPythonDeepLearning.Wehavetoinstallthefollowingsoftwareformakingdeeplearningalgorithms.在本章中,我们将学习为Python
- 探索图形算法的奇妙世界:goraph
孔岱怀
探索图形算法的奇妙世界:goraphgoraphPackagegoraphimplementsgraphdatastructureandalgorithms.项目地址:https://gitcode.com/gh_mirrors/go/goraph在编程领域,数据结构和算法是构建高效应用的基础。今天,我们要向您推荐一款名为【goraph】的开源项目,它是一个用Go语言实现的图形数据结构及其算法库。
- What are some of halcon‘s best algorithms that opencv doesn‘t implement
0010000100
OpenCVopencv人工智能
HALCON,ahighlyoptimizedmachinevisionlibrary,offersarangeofadvancedalgorithmsthatOpenCVeitherdoesn’timplementorhandlesdifferently.SomeofthekeystrengthsofHALCONcomparedtoOpenCVinclude:Shape-BasedMatchin
- Leetcode 1207. Unique Number of Occurrences
小白菜又菜
Leetcode入门题leetcode算法职场和发展
ProblemGivenanarrayofintegersarr,returntrueifthenumberofoccurrencesofeachvalueinthearrayisuniqueorfalseotherwise.AlgorithmSortthearrayandtesttheadjointnumbers.CodeclassSolution:defuniqueOccurrences(se
- 编程练习题目集【目录】
绯樱殇雪
目录PTAc++javapat考试
所有负面情绪都源于你的弱小,唯有强大自己才能够百毒不侵。文章目录一、PTA1.练习(1)中国大学MOOC-陈越、何钦铭-数据结构-起步能力自测题(2)DataStructuresandAlgorithms(English)(3)数据结构与算法题目集(中文)(4)团体程序设计天梯赛-练习集(5)基础编程题目集①函数题②编程题2.考试(1)PAT(BasicLevel)Practice(中文)(2)P
- 超分 Real-ESRGAN 使用笔记
AI算法网奇
深度学习宝典人工智能
效果图目录依赖项:推理入口文件:RealESRGAN_x4plus12g显存不够RealESRGAN_x4plus_anime_6B的效果树枝之间产生了蒙版RealESRNet_x4plus有点模糊2022年开源的GitHub-xinntao/Real-ESRGAN:Real-ESRGANaimsatdevelopingPracticalAlgorithmsforGeneralImage/Vide
- Study Plan For Algorithms - Part11
五月的风与火
StudyPlanForAlgorithmspython算法数据结构
1.剪绳子给定一根长度为n的绳子,请把绳子剪成整数长度的m段(m、n都是整数,n>1并且m>1),每段绳子的长度记为k[0],k[1]…k[m-1]。请问k[0]k[1]…*k[m-1]可能的最大乘积是多少?方法一:defcuttingRope(n):arr=[1]*(n+1)foriinrange(3,n+1):forjinrange(1,i):arr[i]=max(arr[i],j*(i-j)
- Study Plan For Algorithms - Part7
五月的风与火
StudyPlanForAlgorithmspython算法数据结构
1.青蛙跳台阶一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个n级的台阶总共有多少种跳法。计算结果取模1e9+7(1000000007)方法一:defnum_ways(n):ifn<=2:return1else:return(num_ways(n-1)+num_ways(n-2))%1000000007方法二:defnum_ways(n):i=j=1sum_=0k=0whilek
- 遗传算法与深度学习实战(7)——使用遗传算法解决N皇后问题
盼小辉丶
遗传算法与深度学习实战深度学习DEAP遗传算法
遗传算法与深度学习实战(7)——使用遗传算法解决N皇后问题0.前言1.N皇后问题2.解的表示3.遗传算法解决N皇后问题小结系列链接0.前言进化算法(EvolutionaryAlgorithm,EA)和遗传算法(GeneticAlgorithms,GA)已成功解决了许多复杂的设计和布局问题,部分原因是它们采用了受控随机元素的搜索。这通常使得使用EA或GA设计的系统能够超越我们的理解进行创新。在本节中
- CSE101 C++ Introduction to Data Structures and Algorithms
zhuyu0206girl
c++开发语言
CSE101IntroductiontoDataStructuresandAlgorithmsProgrammingAssignment5Inthisprojectyouwillcreateanew,andsomewhatdifferentintegerListADT,thistimeinC++.YouwillusethisListtoperformshufflingoperations,andd
- 不错链接整理
xushuanglu_csdn
提升学习开源
不错链接整理算法https://github.com/MisterBooo/LeetCodeAnimation手把手撕LeetCode题目,扒各种算法套路的裤子https://github.com/labuladong/fucking-algorithm算法学习笔记https://github.com/nonstriater/Learn-Algorithms常用数据结构及其算法的Java实现,包括
- Programming Abstractions in C阅读笔记:p283-p292
c
《ProgrammingAbstractionsinC》学习第72天,p283-p292总结,总计10页。一、技术总结1、anylasisofalgorithms算法分析——即判断程序的效率(efficiency)。2、mathematicalinduction(数学归纳法)3、Big-Onotation(大O标记法)4、constanttime(常量时间)5、lineartime(线性时间)p2
- 【Algorithms 4】算法(第4版)学习笔记 07 - 2.4 优先队列
MichelleChung
算法学习算法java
文章目录前言参考目录学习笔记1:API1.1:实现demo示例1.2:初级实现(有序或无序的数组)2:二叉堆2.1:完全二叉树2.2:二叉堆2.2.1:堆的表示2.2.2:属性2.3:堆算法:由下至上的堆有序化(上浮)2.3.1:swim介绍2.3.2:swim代码实现2.3.3:应用:堆插入节点2.3.4:swim应用代码实现2.3.5:swim应用demo演示2.4:堆算法:由上至下的堆有序化
- 【Algorithms 4】算法(第4版)学习笔记 06 - 2.3 快速排序
MichelleChung
算法学习算法java
文章目录前言参考目录学习笔记1:基本算法1.1:快速排序demo演示1.2:快速排序切分代码实现1.3:实现细节1.4:案例分析1.4.1:最佳案例1.4.2:最坏案例1.4.3:平均案例分析1.5:特征总结1.6:算法优化2:Dijkstra三向切分的快速排序2.1:三向切分demo演示2.2:三向切分代码实现2.3:熵最优3:排序算法小总结前言本章节主要内容是快速排序。快速排序被誉为二十世纪十
- CS50x 2024 - Lecture 3 - Algorithms
dc爱傲雪和技术
计算机科学
TABLEOFCONTENTS00:00:00-Introduction一种统计班上人数的方法,全部站起来,两两配对,一个坐下,循环00:01:01-Overview00:02:58-Attendance00:09:40-LinearSearch00:24:58-BinarySearch二分搜索分而治之的方法00:28:25-RunningTime代表这些算法的效率使用的算法将被描述为这些运动时间
- 设计模式-策略模式 Strategy
中二Espresso
设计模式设计模式策略模式java
策略模式1)原理和实现1、策略的定义2、策略的创建3、策略的使用该模式最常见的应用场景是,利用它来避免冗长的if-else或switch分支判断。不过,它的作用还不止如此。它也可以像模板模式那样,提供框架的扩展点等等。1)原理和实现策略模式,英文全称是StrategyDesignPattern。该模式是这样定义的:Defineafamilyofalgorithms,encapsulateeacho
- 2018年9月份GitHub上最热门的Python项目
小牛学堂
本文我们将和大家介绍GitHub上9月份最受欢迎的11个Python开源项目,在这些项目中,你有在用或用过哪些呢?1.Pythonhttps://github.com/TheAlgorithms/PythonStar14125用Python实现的所有算法,不过创建者表示这些仅用于演示目的。Python标准库中有许多种类的实现,出于性能原因要好得多。2.Algorithm_Interview_Not
- 西瓜书-机器学习5.4 全局最小与局部极小
lestat_black
西瓜书机器学习
两种“最优”:“局部极小”(localminimum)和"全局最小"(globalminimum)对和,若存在使得多组不同参数值初始化多个神经网络使用“模拟退火”:以一定的概率接受比当前解更差的结果,有助于“跳出”局部极小使用随机梯度下降遗传算法(geneticalgorithms)[Goldberg,1989]也常用来训练神经网络以上用于跳出局部极小的技术大多是启发式,理论上商缺乏保障。Gold
- CS170 Artificial Intelligence
nicename5
深度优先算法
Project1:SearchAlgorithmsinaGridEnvironmentandPath-findingCS170ArtificialIntelligence,UCR,Winter20241IntroductionExploretheworldofsearchalgorithmsinagrid-basedenvironment.Inthisproject,youwillimplemen
- 几种智能指针的原理/简单实现
devilisdevil
详细代码放在了:AC/Algorithms/STL/smartpointers/接口说明auto_ptr之后在C++11引入了移动语义,所以后面新出的三个智能指针实现和auto_ptr有比较明显区别auto_ptrhttp://www.cplusplus.com/reference/memory/auto_ptr/是已经在C++11被废弃的指针,其功能对应现在的unique_ptrauto_ptr
- LintCode 3687 · Check If an Array Is a Valid Sequence (二叉树遍历和分治好题)
纸上得来终觉浅 绝知此事要躬行
leetcode算法
3687·CheckIfanArrayIsaValidSequenceAlgorithmsMediumDescriptionGivenabinarytreewitharootnoderoot,wecallthesequenceofnodevaluesinanypathfromtherootnodetoanyleafnodeisa“validsequence”ofthatbinarytree.Now
- java中token的生成与解析
cqwuliu
jAVA工具java开发语言spring
依赖com.auth0java-jwt3.4.0代码如下:packagecom.utils;importcom.auth0.jwt.JWT;importcom.auth0.jwt.JWTVerifier;importcom.auth0.jwt.algorithms.Algorithm;importcom.auth0.jwt.exceptions.JWTVerificationException;i
- 算法大纲
Fitz_Lee
算法大纲:http://www.lydshy.com/wordpress/wp-content/uploads/2017/10/category.pdf计算机科学中最重要的32个算法http://www.infoq.com/cn/news/2012/08/32-most-important-algorithms数据结构字符串,数组,链表,栈,队列,树,图,并查集,散列,优先队列(堆)查找顺序查找,
- 算法复杂度分析(O)
GHope
算法复杂度是指算法在编写成可执行程序后,运行时所需要的资源,资源包括时间资源和内存资源。可以大概理解为操作的次数和数据个数的比例关系。算法复杂度分析O参考《DataStructuresandAlgorithmsinPython》中给的一个例子:考虑计算一个n*n矩阵所有元素的和:这里列举两种方式:#version1total_sum=0foriinrange(n):row_sum[i]=0forj
- NLopt里面的算法
布织岛
Nlopt包含很多优化算法。NLopt中的每个算法都由命名常量标识,被传入NLopt中。TheseconstantsaremostlyoftheformNLOPT_{G,L}{N,D}_xxxx,whereG/Ldenotesglobal/localoptimizationandN/Ddenotesderivative-free/gradient-basedalgorithms,respectiv
- Undefined control sequence.l.113 \LinesNumbered
wzg2016
latexalgorithm
问题:在写小论文时的latex文件里的algorithm模块,复制到毕业论文的latex脚本之后出现以下问题:...!Undefinedcontrolsequence.l.113\LinesNumbered?添加\usepackage[linesnumbered,boxed]{algorithm2e}之后,出现:!LaTeXError:Command\listofalgorithmsalready
- Gensim详细介绍和使用:一个Python文本建模库
Bigcrab__
Python库介绍和使用python
Gensim=“GenerateSimilar”一、安装二、文本预处理2.1中文语料处理2.2英文语料处理2.3BOW语料建立三、模型使用3.1word2vecThealgorithmsinGensim,suchasWord2Vec,FastText,LatentSemanticIndexing(LSI,LSA,LsiModel),LatentDirichletAllocation(LDA,Lda
- 面向对象面向过程
3213213333332132
java
面向对象:把要完成的一件事,通过对象间的协作实现。
面向过程:把要完成的一件事,通过循序依次调用各个模块实现。
我把大象装进冰箱这件事为例,用面向对象和面向过程实现,都是用java代码完成。
1、面向对象
package bigDemo.ObjectOriented;
/**
* 大象类
*
* @Description
* @author FuJian
- Java Hotspot: Remove the Permanent Generation
bookjovi
HotSpot
openjdk上关于hotspot将移除永久带的描述非常详细,http://openjdk.java.net/jeps/122
JEP 122: Remove the Permanent Generation
Author Jon Masamitsu
Organization Oracle
Created 2010/8/15
Updated 2011/
- 正则表达式向前查找向后查找,环绕或零宽断言
dcj3sjt126com
正则表达式
向前查找和向后查找
1. 向前查找:根据要匹配的字符序列后面存在一个特定的字符序列(肯定式向前查找)或不存在一个特定的序列(否定式向前查找)来决定是否匹配。.NET将向前查找称之为零宽度向前查找断言。
对于向前查找,出现在指定项之后的字符序列不会被正则表达式引擎返回。
2. 向后查找:一个要匹配的字符序列前面有或者没有指定的
- BaseDao
171815164
seda
import java.sql.Connection;
import java.sql.DriverManager;
import java.sql.SQLException;
import java.sql.PreparedStatement;
import java.sql.ResultSet;
public class BaseDao {
public Conn
- Ant标签详解--Java命令
g21121
Java命令
这一篇主要介绍与java相关标签的使用 终于开始重头戏了,Java部分是我们关注的重点也是项目中用处最多的部分。
1
- [简单]代码片段_电梯数字排列
53873039oycg
代码
今天看电梯数字排列是9 18 26这样呈倒N排列的,写了个类似的打印例子,如下:
import java.util.Arrays;
public class 电梯数字排列_S3_Test {
public static void main(S
- Hessian原理
云端月影
hessian原理
Hessian 原理分析
一. 远程通讯协议的基本原理
网络通信需要做的就是将流从一台计算机传输到另外一台计算机,基于传输协议和网络 IO 来实现,其中传输协议比较出名的有 http 、 tcp 、 udp 等等, http 、 tcp 、 udp 都是在基于 Socket 概念上为某类应用场景而扩展出的传输协
- 区分Activity的四种加载模式----以及Intent的setFlags
aijuans
android
在多Activity开发中,有可能是自己应用之间的Activity跳转,或者夹带其他应用的可复用Activity。可能会希望跳转到原来某个Activity实例,而不是产生大量重复的Activity。
这需要为Activity配置特定的加载模式,而不是使用默认的加载模式。 加载模式分类及在哪里配置
Activity有四种加载模式:
standard
singleTop
- hibernate几个核心API及其查询分析
antonyup_2006
html.netHibernatexml配置管理
(一) org.hibernate.cfg.Configuration类
读取配置文件并创建唯一的SessionFactory对象.(一般,程序初始化hibernate时创建.)
Configuration co
- PL/SQL的流程控制
百合不是茶
oraclePL/SQL编程循环控制
PL/SQL也是一门高级语言,所以流程控制是必须要有的,oracle数据库的pl/sql比sqlserver数据库要难,很多pl/sql中有的sqlserver里面没有
流程控制;
分支语句 if 条件 then 结果 else 结果 end if ;
条件语句 case when 条件 then 结果;
循环语句 loop
- 强大的Mockito测试框架
bijian1013
mockito单元测试
一.自动生成Mock类 在需要Mock的属性上标记@Mock注解,然后@RunWith中配置Mockito的TestRunner或者在setUp()方法中显示调用MockitoAnnotations.initMocks(this);生成Mock类即可。二.自动注入Mock类到被测试类 &nbs
- 精通Oracle10编程SQL(11)开发子程序
bijian1013
oracle数据库plsql
/*
*开发子程序
*/
--子程序目是指被命名的PL/SQL块,这种块可以带有参数,可以在不同应用程序中多次调用
--PL/SQL有两种类型的子程序:过程和函数
--开发过程
--建立过程:不带任何参数
CREATE OR REPLACE PROCEDURE out_time
IS
BEGIN
DBMS_OUTPUT.put_line(systimestamp);
E
- 【EhCache一】EhCache版Hello World
bit1129
Hello world
本篇是EhCache系列的第一篇,总体介绍使用EhCache缓存进行CRUD的API的基本使用,更细节的内容包括EhCache源代码和设计、实现原理在接下来的文章中进行介绍
环境准备
1.新建Maven项目
2.添加EhCache的Maven依赖
<dependency>
<groupId>ne
- 学习EJB3基础知识笔记
白糖_
beanHibernatejbosswebserviceejb
最近项目进入系统测试阶段,全赖袁大虾领导有力,保持一周零bug记录,这也让自己腾出不少时间补充知识。花了两天时间把“传智播客EJB3.0”看完了,EJB基本的知识也有些了解,在这记录下EJB的部分知识,以供自己以后复习使用。
EJB是sun的服务器端组件模型,最大的用处是部署分布式应用程序。EJB (Enterprise JavaBean)是J2EE的一部分,定义了一个用于开发基
- angular.bootstrap
boyitech
AngularJSAngularJS APIangular中文api
angular.bootstrap
描述:
手动初始化angular。
这个函数会自动检测创建的module有没有被加载多次,如果有则会在浏览器的控制台打出警告日志,并且不会再次加载。这样可以避免在程序运行过程中许多奇怪的问题发生。
使用方法: angular .
- java-谷歌面试题-给定一个固定长度的数组,将递增整数序列写入这个数组。当写到数组尾部时,返回数组开始重新写,并覆盖先前写过的数
bylijinnan
java
public class SearchInShiftedArray {
/**
* 题目:给定一个固定长度的数组,将递增整数序列写入这个数组。当写到数组尾部时,返回数组开始重新写,并覆盖先前写过的数。
* 请在这个特殊数组中找出给定的整数。
* 解答:
* 其实就是“旋转数组”。旋转数组的最小元素见http://bylijinnan.iteye.com/bl
- 天使还是魔鬼?都是我们制造
ducklsl
生活教育情感
----------------------------剧透请原谅,有兴趣的朋友可以自己看看电影,互相讨论哦!!!
从厦门回来的动车上,无意中瞟到了书中推荐的几部关于儿童的电影。当然,这几部电影可能会另大家失望,并不是类似小鬼当家的电影,而是关于“坏小孩”的电影!
自己挑了两部先看了看,但是发现看完之后,心里久久不能平
- [机器智能与生物]研究生物智能的问题
comsci
生物
我想,人的神经网络和苍蝇的神经网络,并没有本质的区别...就是大规模拓扑系统和中小规模拓扑分析的区别....
但是,如果去研究活体人类的神经网络和脑系统,可能会受到一些法律和道德方面的限制,而且研究结果也不一定可靠,那么希望从事生物神经网络研究的朋友,不如把
- 获取Android Device的信息
dai_lm
android
String phoneInfo = "PRODUCT: " + android.os.Build.PRODUCT;
phoneInfo += ", CPU_ABI: " + android.os.Build.CPU_ABI;
phoneInfo += ", TAGS: " + android.os.Build.TAGS;
ph
- 最佳字符串匹配算法(Damerau-Levenshtein距离算法)的Java实现
datamachine
java算法字符串匹配
原文:http://www.javacodegeeks.com/2013/11/java-implementation-of-optimal-string-alignment.html------------------------------------------------------------------------------------------------------------
- 小学5年级英语单词背诵第一课
dcj3sjt126com
englishword
long 长的
show 给...看,出示
mouth 口,嘴
write 写
use 用,使用
take 拿,带来
hand 手
clever 聪明的
often 经常
wash 洗
slow 慢的
house 房子
water 水
clean 清洁的
supper 晚餐
out 在外
face 脸,
- macvim的使用实战
dcj3sjt126com
macvim
macvim用的是mac里面的vim, 只不过是一个GUI的APP, 相当于一个壳
1. 下载macvim
https://code.google.com/p/macvim/
2. 了解macvim
:h vim的使用帮助信息
:h macvim
- java二分法查找
蕃薯耀
java二分法查找二分法java二分法
java二分法查找
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
蕃薯耀 2015年6月23日 11:40:03 星期二
http:/
- Spring Cache注解+Memcached
hanqunfeng
springmemcached
Spring3.1 Cache注解
依赖jar包:
<!-- simple-spring-memcached -->
<dependency>
<groupId>com.google.code.simple-spring-memcached</groupId>
<artifactId>simple-s
- apache commons io包快速入门
jackyrong
apache commons
原文参考
http://www.javacodegeeks.com/2014/10/apache-commons-io-tutorial.html
Apache Commons IO 包绝对是好东西,地址在http://commons.apache.org/proper/commons-io/,下面用例子分别介绍:
1) 工具类
2
- 如何学习编程
lampcy
java编程C++c
首先,我想说一下学习思想.学编程其实跟网络游戏有着类似的效果.开始的时候,你会对那些代码,函数等产生很大的兴趣,尤其是刚接触编程的人,刚学习第一种语言的人.可是,当你一步步深入的时候,你会发现你没有了以前那种斗志.就好象你在玩韩国泡菜网游似的,玩到一定程度,每天就是练级练级,完全是一个想冲到高级别的意志力在支持着你.而学编程就更难了,学了两个月后,总是觉得你好象全都学会了,却又什么都做不了,又没有
- 架构师之spring-----spring3.0新特性的bean加载控制@DependsOn和@Lazy
nannan408
Spring3
1.前言。
如题。
2.描述。
@DependsOn用于强制初始化其他Bean。可以修饰Bean类或方法,使用该Annotation时可以指定一个字符串数组作为参数,每个数组元素对应于一个强制初始化的Bean。
@DependsOn({"steelAxe","abc"})
@Comp
- Spring4+quartz2的配置和代码方式调度
Everyday都不同
代码配置spring4quartz2.x定时任务
前言:这些天简直被quartz虐哭。。因为quartz 2.x版本相比quartz1.x版本的API改动太多,所以,只好自己去查阅底层API……
quartz定时任务必须搞清楚几个概念:
JobDetail——处理类
Trigger——触发器,指定触发时间,必须要有JobDetail属性,即触发对象
Scheduler——调度器,组织处理类和触发器,配置方式一般只需指定触发
- Hibernate入门
tntxia
Hibernate
前言
使用面向对象的语言和关系型的数据库,开发起来很繁琐,费时。由于现在流行的数据库都不面向对象。Hibernate 是一个Java的ORM(Object/Relational Mapping)解决方案。
Hibernte不仅关心把Java对象对应到数据库的表中,而且提供了请求和检索的方法。简化了手工进行JDBC操作的流程。
如
- Math类
xiaoxing598
Math
一、Java中的数字(Math)类是final类,不可继承。
1、常数 PI:double圆周率 E:double自然对数
2、截取(注意方法的返回类型) double ceil(double d) 返回不小于d的最小整数 double floor(double d) 返回不大于d的整最大数 int round(float f) 返回四舍五入后的整数 long round
![]() 的问题所花费的时间(或者所需步骤的数目)可以表示为:
的问题所花费的时间(或者所需步骤的数目)可以表示为:![]() 。当
。当![]() 增大时,
增大时,![]() 项将开始占主导地位,而其他各项可以被忽略。 举例说明:当
项将开始占主导地位,而其他各项可以被忽略。 举例说明:当![]() ,
,![]() 项是
项是 ![]() 项的1000倍大,因此在大多数场合下,省略后者对表达式的值的影响将是可以忽略不计的。
项的1000倍大,因此在大多数场合下,省略后者对表达式的值的影响将是可以忽略不计的。![]() 项的系数也是无关紧要的。例如:一个包含
项的系数也是无关紧要的。例如:一个包含![]() 或
或![]() 项的表达式,即使
项的表达式,即使 ![]() ,假定
,假定 ![]() ,一旦
,一旦![]() 增长到大于1,000,000,后者就会一直超越前者(
增长到大于1,000,000,后者就会一直超越前者(![]() )。
)。![]() 阶(平方阶)的时间复杂度。
阶(平方阶)的时间复杂度。![]() 的泰勒展开:
的泰勒展开:![]() 足够接近于0,那么误差
足够接近于0,那么误差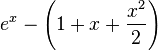 的绝对值小于
的绝对值小于![]() 的某一常数倍。
的某一常数倍。![]() 和
和![]() ,定义:
,定义: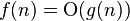 ,条件为:存在正实数
,条件为:存在正实数 和
和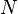 ,使得对于所有的
,使得对于所有的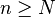 ,有
,有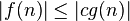
![]() 足够大,大过一个特定的
足够大,大过一个特定的![]() 时,且存在一个正数
时,且存在一个正数![]() ,使得
,使得![]() 不大于
不大于![]() ,则
,则![]() 是
是![]() 的
的![]() 表示。
表示。![]() 和
和![]() 的关系可以理解为
的关系可以理解为![]() 是
是![]() 的一个上界,也可以理解为
的一个上界,也可以理解为![]() 最终至多增涨的速度与
最终至多增涨的速度与![]() 一样快,但不会超过
一样快,但不会超过![]() 的增涨速度。
的增涨速度。![]() 趋近于无穷大的情况下,增长得慢的函数列在上面。
趋近于无穷大的情况下,增长得慢的函数列在上面。![]() 是一个任意常数。
是一个任意常数。![\begin{cases}f(\nu)=\Omicron[g(\nu)]\\g(\nu)=\Omega[f(\nu)]\end{cases}](http://img.e-com-net.com/image/info8/597180a22ba249bcbcda7bdbe9cc227f.png)
![\begin{cases}f(\nu)=\Omicron[g(\nu)]\\f(\nu)=\Omega[g(\nu)]\end{cases}](http://img.e-com-net.com/image/info8/64626dc08a184efebeba545215cf26ef.png)