SiameseFC和CFNet细节笔记
这两篇文章出自牛津大学同一个实验室,一个发表在ECCV2016,一个发表在CVPR2017,下载CFNet的matlab代码中会有改进版的SiamFC代码,也就是论文中提到的baseline-conv5,SiamFC的TensorFlow版本代码也是这个框架的。
看代码的过程中需要对论文熟悉,就再看了一遍这两篇文章,发现有许多细节需要记录下来。
SiameseFC:http://www.robots.ox.ac.uk/~luca/siamese-fc.html
CFNet:http://www.robots.ox.ac.uk/~luca/cfnet.html
SiameseFC
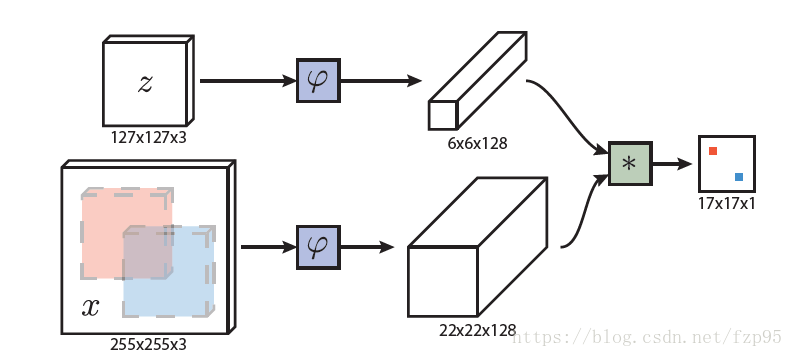
这是SiamFC的框架图,注意最后输出的是一个17x17的响应图,图上的每一点对应的是搜索图像255x255的一个区域。
平移算子 ( L τ x ) [ u ] = x [ u − τ ] (L_\tau x)[u]=x[u-\tau ] (Lτx)[u]=x[u−τ]
h ( L k τ x ) = L τ h ( x ) h(L_{k\tau }x)=L_\tau h(x) h(Lkτx)=Lτh(x)
训练
网络的初始参数借鉴了MSRA何恺明的文章,参数均服从高斯分布
网络的基础结构是AlexNet,一共五层,如下:
C1:96个11*11*3的卷积核,步长为4;
C2:256个5*5*48的卷积核,步长为1;
C3:384个3*3*256的卷积核,步长为1;
C4:384个3*3*192的卷积核,步长为1;
C5:256个3*3*192的卷积核,步长为1。
损失函数:
l ( y , v ) = l o g ( 1 + e x p ( − y v ) ) l(y,v)=log(1+exp(-yv)) l(y,v)=log(1+exp(−yv))
L ( y , v ) = 1 ∣ D ∣ ∑ u ∈ D l ( y [ u ] , v [ u ] ) L(y,v)= \frac{1}{|D|} \sum_{u\in D}l(y[u],v[u]) L(y,v)=∣D∣1u∈D∑l(y[u],v[u])
u ∈ D u\in D u∈D是得分图谱的位置, v [ u ] v[u] v[u]是这个位置做相关操作后的值 v = f ( z , x ; θ ) v=f(z,x;\theta ) v=f(z,x;θ), y [ u ] y[u] y[u]是这个位置的标签,取{+1,-1}。
y [ u ] = { + 1 if k ∥ u − c ∥ ≤ R − 1 otherwise y[u]=\begin{cases} +1 & \text{ if } k\left \| u-c \right \|\leq R \\ -1 & \text{ otherwise } \end{cases} y[u]={+1−1 if k∥u−c∥≤R otherwise
k是网络的步长,当小于图像中心一定距离时,取正标签。
最小化这个 L ( y , v ) L(y,v) L(y,v),通过随机梯度下降法,求出网络的参数 θ \theta θ。
训练集是ILSVRC2015,为了更好的适应对训练集做了一些处理,剔除了一些占整幅画面太大或太小的目标,还剔除了一下距离图片边缘太近的目标。处理后的数据集包含2820个视频,843371个目标。
训练的图像对(pairs)包含两帧的图像,最多相隔T帧,因为是全卷积,学习倾向在图像中心,所以训练的目标都在图像的中心,如下图:

对图像的尺寸做了归一化,不改变图像的纵横比,多出的部分用图像的RGB均值填充。
网络结构中没有padding
跟踪
本文只是证明了全卷积孪生网络做跟踪的有效性,以及在imgnet上训练的泛化能力,所以we do not update a model or maintain a memory of past appearances, we do not incorporate additional cues such as optical flow or colour histograms, and we do not re fine our prediction with bounding box regression.
尽管如此,它也表现出不错的性能。
作者在得分图上加入余弦窗来惩罚过大的距离。
跟踪时, φ ( x ) \varphi(x) φ(x)只算一次,也就是样例图像只是第一帧。
为了应对目标的尺度变化,搜索分支的图像选取了多个尺度。其中初始的SiamFC采用了5种尺度,分别是 1.02 5 { − 2 , − 1 , 0 , 1 , 2 } 1.025^{\left \{ -2,-1,0,1,2 \right \}} 1.025{−2,−1,0,1,2},针对这些尺度采用了以0.35为步长的线性函数作为抑制。另外SiamFC-3s则是采用了3种尺度 1.0 3 { − 1 , 0 , 1 } 1.03^{\left \{ -1,0,1 \right \}} 1.03{−1,0,1}。哪种尺度得分高选哪个。
通过双三次插值上采样得分图谱从17x17变为272x272,来定位目标。双三次插值的原理网上可以搜到。
疑问:bounding box怎么确定的?
CFNet
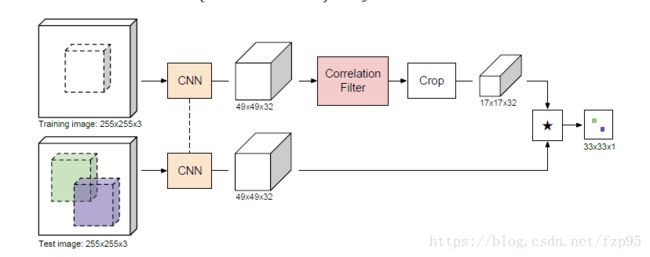
在孪生网络结构的基础上加了相关滤波器,在特征提取上,上下两分支的网络还是一模一样的,不同的是在样例分支上,也就是Training Image分支上加了相关滤波器,所以上面的分支出来的就是相关滤波器 w w w。本文的核心就是将CF可微,视为网络中的一层,使之可以反向传播,以至于整个网络可以端到端的训练。
我们知道,SiamFC的速度很快,但是精度方面不太好,因为全卷积的结构缺少特定目标判别性的信息
加入CF,也就是相关滤波器,一是通过解岭回归问题,它的判别性比较好,二是它利用循环矩阵的性质在傅里叶域计算很快,可以在线跟踪。所以作者将CNN和CF结合了起来,可以端到端训练。
通过下面的公式,算出相关滤波器:
arg min w 1 2 n ∥ w ⋆ x − y ∥ 2 + λ 2 ∥ w ∥ 2 \arg \min_{w} \frac{1}{2n}\left \| w\star x-y \right \|^2+\frac{\lambda }{2}\left \| w \right \|^2 argwmin2n1∥w⋆x−y∥2+2λ∥w∥2
w w w是相关滤波器, y y y是 x x x位置的高斯响应, ⋆ \star ⋆ 代表的是互相关。
至于怎么实现端到端的,具体细节可以看论文,推导过程中利用了将上述方程转化为的拉格朗日对偶问题,再进行的微分。
作者还提到,其实 y y y是可以通过反向传播优化的,但是效果并不好,所以干脆就用了高斯响应。
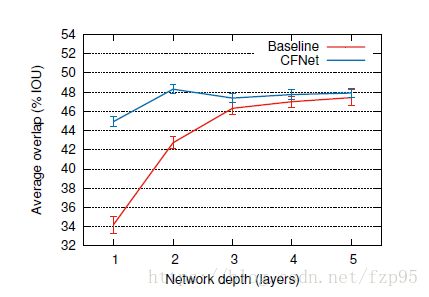
这张图是CFNet和Baseline的比较,Baseline和之前提出的SiamFC还是有少许不同的,总步长由8改为了4,防止得出的相关滤波器图谱过小,最后的特征图通道数也限制在了32层。
通过对比可以看出,加入相关滤波器的CFNet的性能,并不是随着网络的加深而提高,甚至出现了降低,说明相关滤波器主要需要的是浅层的特征信息。在网络层数较深的情况下,和SiamFC的性能差异不大,SiamFC是全卷积网络,在网络结构上还是有很大改进空间的,最近出了很多以此为baseline的论文印证了这一点。