深入浅出的强化学习笔记(二)——使用OpenAI Gym实现游戏AI
深入浅出的强化学习笔记(二)——使用OpenAI Gym实现游戏AI
OpenAI Gym是一个用于研发和比较强化学习算法的Python库,我们可以通过以下命令来安装它。
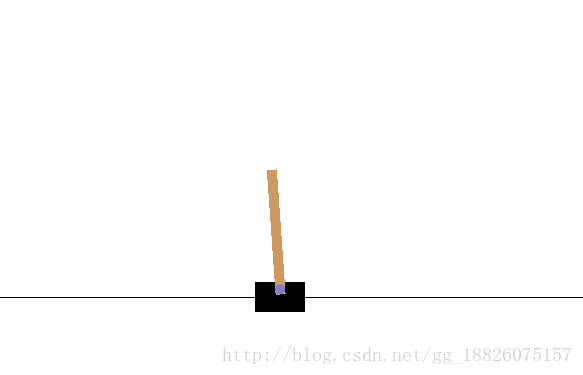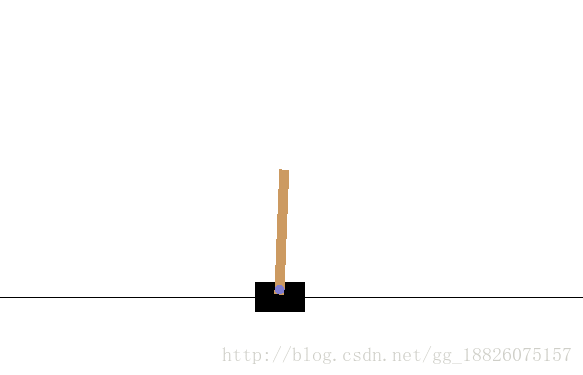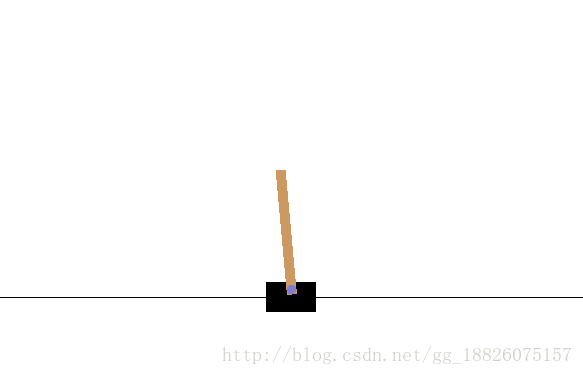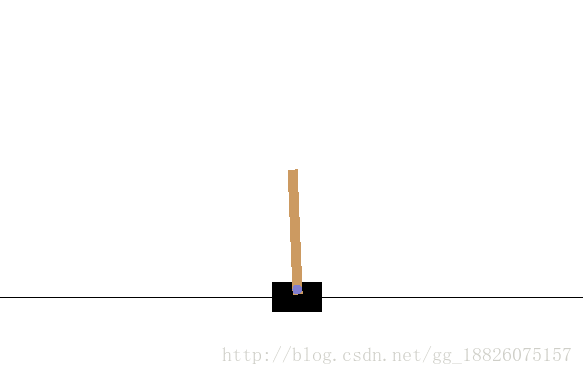
$ pip install gym下面我们将尝试训练一个AI来帮我们完成一款游戏——CartPole-v0,从而掌握强化学习的一个重要分支——Q-learning。
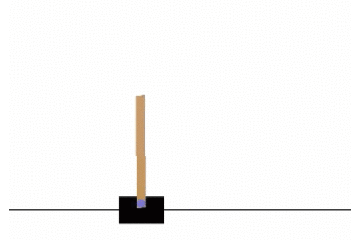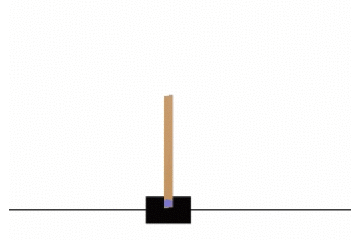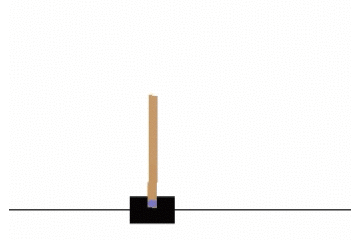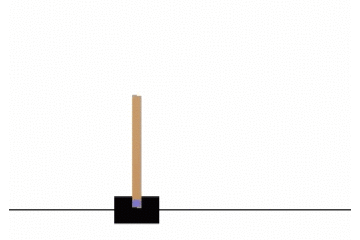
游戏规则很简单,我们要操纵我们的小车左右移动,使它上面不断变长的木棒能够保持平衡。
首先我们要从该游戏中抽离出各种元素,以套用我们的强化学习模型。
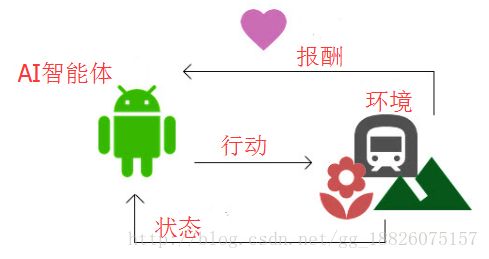
游戏的全过程可以理解为AI智能体和环境之间的互动,我们把其中复杂的因素抽象为三个变量——报酬、行动、状态。
状态
状态应该包括以下4个因素:
| 编号 | 名称 | 最小值 | 最大值 |
|---|---|---|---|
| 0 | 小车的位置 | -2.4 | 2.4 |
| 1 | 小车的速度 | -inf | inf |
| 2 | 木棒的角度 | -41.8° | 41.8° |
| 3 | 木棒的速度 | -inf | inf |
行动
对于某一个状态s采取的行动A(s)应该包括以下两种:
| 编号 | 名称 |
|---|---|
| 0 | 小车往左移动 |
| 1 | 小车往右移动 |
报酬
木棒每保持平衡1个时间步,就得到1分。
每一场游戏的最高得分为200分
每一场游戏的结束条件:木棒倾斜角度大于41.8°或者已经达到200分
最终获胜条件为:最近100场游戏的平均得分高于195
代码实现(雏形)
下面让我们使用OpenAI Gym根据上面的思路完成代码的雏形,并保存为cartpole.py。
import gym
import numpy as np
env = gym.make('CartPole-v0')
max_number_of_steps = 200 # 每一场游戏的最高得分
#---------获胜的条件是最近100场平均得分高于195-------------
goal_average_steps = 195
num_consecutive_iterations = 100
#----------------------------------------------------------
num_episodes = 5000 # 共进行5000场游戏
last_time_steps = np.zeros(num_consecutive_iterations) # 只存储最近100场的得分(可以理解为是一个容量为100的栈)
# 重复进行一场场的游戏
for episode in range(num_episodes):
observation = env.reset() # 初始化本场游戏的环境
episode_reward = 0 # 初始化本场游戏的得分
# 一场游戏分为一个个时间步
for t in range(max_number_of_steps):
env.render() # 更新并渲染游戏画面
action = np.random.choice([0, 1]) # 随机决定小车运动的方向
observation, reward, done, info = env.step(action) # 获取本次行动的反馈结果
episode_reward += reward
if done:
print('%d Episode finished after %f time steps / mean %f' % (episode, t + 1, last_time_steps.mean()))
last_time_steps = np.hstack((last_time_steps[1:], [episode_reward])) # 更新最近100场游戏的得分stack
break
# 如果最近100场平均得分高于195
if (last_time_steps.mean() >= goal_average_steps):
print('Episode %d train agent successfuly!' % episode)
break
print('Failed!')上面的代码只是使用np.random.choice([0, 1])随机决定小车运动的方向,并没有进行任何的智能学习。
运行代码,发现每场游戏的平均得分仅22左右。
代码实现(Q-learning)
让我们来利用每次行动后得到的反馈进行强化学习建模,首先我们选择Q-learning算法,那么如果在时间步t时,状态为 st ,我们采取的行动为 at ,本次行动的有利程度记为 Q(st,at) ,则有下式:
上面的 α 被称为学习系数, γ 被称为报酬衰减系数, rt 为时间步为t时得到的报酬(因为报酬仅与时间有关)。
import gym
import numpy as np
env = gym.make('CartPole-v0')
max_number_of_steps = 200 # 每一场游戏的最高得分
#---------获胜的条件是最近100场平均得分高于195-------------
goal_average_steps = 195
num_consecutive_iterations = 100
#----------------------------------------------------------
num_episodes = 5000 # 共进行5000场游戏
last_time_steps = np.zeros(num_consecutive_iterations) # 只存储最近100场的得分(可以理解为是一个容量为100的栈)
# q_table是一个256*2的二维数组
# 离散化后的状态共有4^4=256中可能的取值,每种状态会对应一个行动
# q_table[s][a]就是当状态为s时作出行动a的有利程度评价值
# 我们的AI模型要训练学习的就是这个映射关系表
q_table = np.random.uniform(low=-1, high=1, size=(4 ** 4, env.action_space.n))
# 分箱处理函数,把[clip_min,clip_max]区间平均分为num段,位于i段区间的特征值x会被离散化为i
def bins(clip_min, clip_max, num):
return np.linspace(clip_min, clip_max, num + 1)[1:-1]
# 离散化处理,将由4个连续特征值组成的状态矢量转换为一个0~~255的整数离散值
def digitize_state(observation):
# 将矢量打散回4个连续特征值
cart_pos, cart_v, pole_angle, pole_v = observation
# 分别对各个连续特征值进行离散化(分箱处理)
digitized = [np.digitize(cart_pos, bins=bins(-2.4, 2.4, 4)),
np.digitize(cart_v, bins=bins(-3.0, 3.0, 4)),
np.digitize(pole_angle, bins=bins(-0.5, 0.5, 4)),
np.digitize(pole_v, bins=bins(-2.0, 2.0, 4))]
# 将4个离散值再组合为一个离散值,作为最终结果
return sum([x * (4 ** i) for i, x in enumerate(digitized)])
# 根据本次的行动及其反馈(下一个时间步的状态),返回下一次的最佳行动
def get_action(state, action, observation, reward):
next_state = digitize_state(observation) # 获取下一个时间步的状态,并将其离散化
next_action = np.argmax(q_table[next_state]) # 查表得到最佳行动
#-------------------------------------训练学习,更新q_table----------------------------------
alpha = 0.2 # 学习系数α
gamma = 0.99 # 报酬衰减系数γ
q_table[state, action] = (1 - alpha) * q_table[state, action] + alpha * (reward + gamma * q_table[next_state, next_action])
# -------------------------------------------------------------------------------------------
return next_action, next_state
# 重复进行一场场的游戏
for episode in range(num_episodes):
observation = env.reset() # 初始化本场游戏的环境
state = digitize_state(observation) # 获取初始状态值
action = np.argmax(q_table[state]) # 根据状态值作出行动决策
episode_reward = 0
# 一场游戏分为一个个时间步
for t in range(max_number_of_steps):
env.render() # 更新并渲染游戏画面
observation, reward, done, info = env.step(action) # 获取本次行动的反馈结果
action, state = get_action(state, action, observation, reward) # 作出下一次行动的决策
episode_reward += reward
if done:
print('%d Episode finished after %f time steps / mean %f' % (episode, t + 1, last_time_steps.mean()))
last_time_steps = np.hstack((last_time_steps[1:], [episode_reward])) # 更新最近100场游戏的得分stack
break
# 如果最近100场平均得分高于195
if (last_time_steps.mean() >= goal_average_steps):
print('Episode %d train agent successfuly!' % episode)
break
print('Failed!')运行代码,发现虽然分数是有所提高,但效果并没有十分显著,随着训练的进行,在过拟合之前,最高的平均分数也仅有32左右。
代码实现(Q-learning改良版)
算法表现不佳的原因在于,采用的是“仅利用”法,即每一次的决策都是选择当前最优的行动,然而这个“最优的行动”是模型一厢情愿的,并没有作充足的探索。
因为模型的每一次决策都“太贪心”了,目光短浅,必须要让他“跳出舒适区”,大胆试错,然后随着时间的推移,自然能找出真正的最佳决策。
为了实现我们的想法,我们引入ε-贪心策略,即每次要移动小车时,以ε的概率以均匀概率随机选一个方向进行移动;以1-ε的概率选择目前为止探索到的对于当前状态的最佳行动方向进行移动。
我们把get_action函数更改为下面的这个样子:
def get_action(state, action, observation, reward):
next_state = digitize_state(observation)
epsilon = 0.2 # ε-贪心策略中的ε
if epsilon <= np.random.uniform(0, 1):
next_action = np.argmax(q_table[next_state])
else:
next_action = np.random.choice([0, 1])
# 后面的内容跟之前一样可惜,效果并没有十分理想,考虑是因为没有给ε设置一个衰减系数。因为随着探索的进行,我们模型“见识”会越来越广,这时候要做的应该是不断缩小范围锁定真正的最优解,应该越来越趋向于选择以往经验验证过的最优行动。
一直无限制地扩大选择空间并不是明智的选择。再把get_action函数作如下修改:
def get_action(state, action, observation, reward, episode):
next_state = digitize_state(observation)
epsilon = 0.5 * (0.99 ** episode)
# 后面的内容跟上面一样因为增加了一个参数,其调用方式也要稍作改变:
action, state = get_action(state, action, observation, reward, episode)很可惜,效果仍然不甚理想。
代码实现(Q-learning终极版)
最后我们考虑修改报酬评价函数,对于一些直接导致最终失败的错误行动,其报酬值要减200,让模型懂得悬崖勒马,这样每一次快要崩盘时,模型总能作出最正确的补救动作,即使平时有点乱来也“无伤大雅”。
# ...
observation, reward, done, info = env.step(action)
# 对致命错误行动进行极大力度的惩罚,让模型恨恨地吸取教训
if done:
reward = -200
action, state = get_action(state, action, observation, reward, episode)
if done:
print('%d Episode finished after %f time steps / mean %f' % (episode, t + 1,
last_time_steps.mean()))
last_time_steps = np.hstack((last_time_steps[1:], [t + 1]))
break
# ...终于,我们的模型在经过大约1000场的游戏后,终于完全“开窍”了,平均分数能达到了195。
最终版代码已上传到github
https://github.com/gh877916059/Reinforcement-learning-demos-annotated