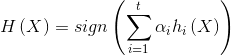简单易学的机器学习算法——AdaBoost
一、集成方法(Ensemble Method)
集成方法主要包括Bagging和Boosting两种方法,随机森林算法是基于Bagging思想的机器学习算法,在Bagging方法中,主要通过对训练数据集进行随机采样,以重新组合成不同的数据集,利用弱学习算法对不同的新数据集进行学习,得到一系列的预测结果,对这些预测结果做平均或者投票做出最终的预测。AdaBoost算法和GBDT(Gradient Boost Decision Tree,梯度提升决策树)算法是基于Boosting思想的机器学习算法。在Boosting思想中是通过对样本进行不同的赋值,对错误学习的样本的权重设置的较大,这样,在后续的学习中集中处理难学的样本,最终得到一系列的预测结果,每个预测结果有一个权重,较大的权重表示该预测效果较好,详细的思想可见博文“简单易学的机器学习算法——集成方法(Ensemble Method)”。
二、AdaBoost算法思想
AdaBoost算法是基于Boosting思想的机器学习算法,其中AdaBoost是Adaptive Boosting的缩写,AdaBoost是一种迭代型的算法,其核心思想是针对同一个训练集训练不同的学习算法,即弱学习算法,然后将这些弱学习算法集合起来,构造一个更强的最终学习算法。
为了构造出一个强的学习算法,首先需要选定一个弱学习算法,并利用同一个训练集不断训练弱学习算法,以提升弱学习算法的性能。在AdaBoost算法中,有两个权重,第一个数训练集中每个样本有一个权重,称为样本权重,用向量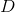 表示;另一个是每一个弱学习算法具有一个权重,用向量
表示;另一个是每一个弱学习算法具有一个权重,用向量 表示。假设有
表示。假设有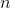 个样本的训练集
个样本的训练集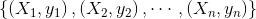 ,初始时,设定每个样本的权重是相等的,即
,初始时,设定每个样本的权重是相等的,即 ,利用第一个弱学习算法
,利用第一个弱学习算法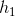 对其进行学习,学习完成后进行错误率
对其进行学习,学习完成后进行错误率 的统计:
的统计:
其中,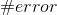 表示被错误分类的样本数目,
表示被错误分类的样本数目,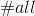 表示所有样本的数目。这样便可以利用错误率
表示所有样本的数目。这样便可以利用错误率 计算弱学习算法
计算弱学习算法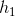 的权重
的权重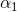 :
:
在第一次学习完成后,需要重新调整样本的权重,以使得在第一分类中被错分的样本的权重,使得在接下来的学习中可以重点对其进行学习:
其中,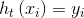 表示对第
表示对第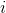 个样本训练正确,
个样本训练正确, 表示对第
表示对第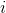 个样本训练错误。
个样本训练错误。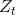 是一个归一化因子:
是一个归一化因子:
这样进行第二次的学习,当学习 轮后,得到了
轮后,得到了 个弱学习算法
个弱学习算法 及其权重
及其权重 。对新的分类数据,分别计算
。对新的分类数据,分别计算 个弱分类器的输出
个弱分类器的输出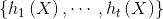 ,最终的AdaBoost算法的输出结果为:
,最终的AdaBoost算法的输出结果为:
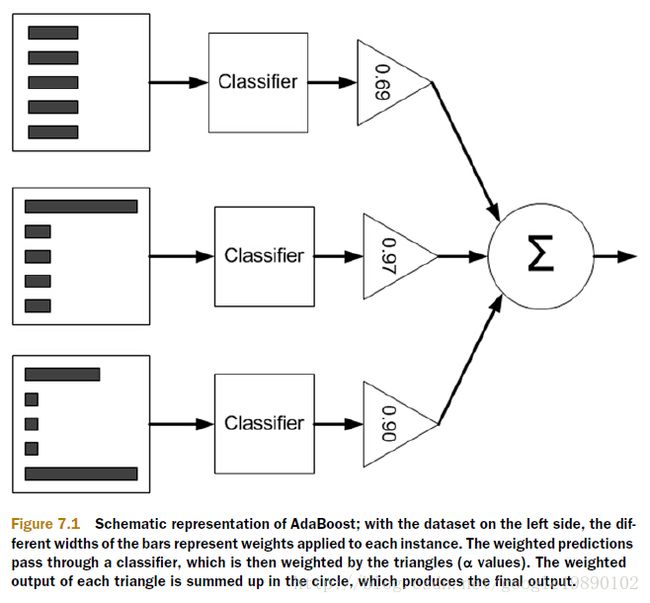
其中,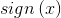 是符号函数。具体过程可见下图所示:
是符号函数。具体过程可见下图所示:
(图片来自参考文件1)
三、AdaBoost算法流程
上述为AdaBoost的基本原理,下面给出AdaBoost算法的流程:
(来自参考文献2)
四、实际的例子
AdaBoost
算法是一种具有很高精度的分类器,其实
AdaBoost
算法提供的是一种框架,在这种框架下,我们可以使用不同的弱分类器,通过
AdaBoost
框架构建出强分类器。下面我们使用单层决策树构建一个分类器处理如下的分类问题:
决策树算法主要有
ID3
,
C4.5
和
CART
,其中
ID3
和
C4.5
主要用于分类,
CART
可以解决回归问题。
ID3
算法可见博文“简单易学的机器学习算法——决策树之ID3算法”,
CART
算法可见博文“简单易学的机器学习算法——CART之回归树”。对于单层决策树是无法求解上面这样的问题的。
Python
代码
#coding:UTF-8
'''
Created on 2015年6月15日
@author: zhaozhiyong
'''
from numpy import *
def loadSimpleData():
datMat = mat([[1., 2.1],
[2., 1.1],
[1.3, 1.],
[1., 1.],
[2., 1.]])
classLabels = mat([1.0, 1.0, -1.0, -1.0, 1.0])
return datMat, classLabels
def singleStumpClassipy(dataMat, dim, threshold, thresholdIneq):
classMat = ones((shape(dataMat)[0], 1))
#根据thresholdIneq划分出不同的类,在'-1'和'1'之间切换
if thresholdIneq == 'left':#在threshold左侧的为'-1'
classMat[dataMat[:, dim] <= threshold] = -1.0
else:
classMat[dataMat[:, dim] > threshold] = -1.0
return classMat
def singleStump(dataArr, classLabels, D):
dataMat = mat(dataArr)
labelMat = mat(classLabels).T
m, n = shape(dataMat)
numSteps = 10.0
bestStump = {}
bestClasEst = zeros((m, 1))
minError = inf
for i in xrange(n):#对每一个特征
#取第i列特征的最小值和最大值,以确定步长
rangeMin = dataMat[:, i].min()
rangeMax = dataMat[:, i].max()
stepSize = (rangeMax - rangeMin) / numSteps
for j in xrange(-1, int(numSteps) + 1):
#不确定是哪个属于类'-1',哪个属于类'1',分两种情况
for inequal in ['left', 'right']:
threshold = rangeMin + j * stepSize#得到每个划分的阈值
predictionClass = singleStumpClassipy(dataMat, i, threshold, inequal)
errorMat = ones((m, 1))
errorMat[predictionClass == labelMat] = 0
weightedError = D.T * errorMat#D是每个样本的权重
if weightedError < minError:
minError = weightedError
bestClasEst = predictionClass.copy()
bestStump['dim'] = i
bestStump['threshold'] = threshold
bestStump['inequal'] = inequal
return bestStump, minError, bestClasEst
def adaBoostTrain(dataArr, classLabels, G):
weakClassArr = []
m = shape(dataArr)[0]#样本个数
#初始化D,即每个样本的权重
D = mat(ones((m, 1)) / m)
aggClasEst = mat(zeros((m, 1)))
for i in xrange(G):#G表示的是迭代次数
bestStump, minError, bestClasEst = singleStump(dataArr, classLabels, D)
print 'D:', D.T
#计算分类器的权重
alpha = float(0.5 * log((1.0 - minError) / max(minError, 1e-16)))
bestStump['alpha'] = alpha
weakClassArr.append(bestStump)
print 'bestClasEst:', bestClasEst.T
#重新计算每个样本的权重D
expon = multiply(-1 * alpha * mat(classLabels).T, bestClasEst)
D = multiply(D, exp(expon))
D = D / D.sum()
aggClasEst += alpha * bestClasEst
print 'aggClasEst:', aggClasEst
aggErrors = multiply(sign(aggClasEst) != mat(classLabels).T, ones((m, 1)))
errorRate = aggErrors.sum() / m
print 'total error:', errorRate
if errorRate == 0.0:
break
return weakClassArr
def adaBoostClassify(testData, weakClassify):
dataMat = mat(testData)
m = shape(dataMat)[0]
aggClassEst = mat(zeros((m, 1)))
for i in xrange(len(weakClassify)):#weakClassify是一个列表
classEst = singleStumpClassipy(dataMat, weakClassify[i]['dim'], weakClassify[i]['threshold'], weakClassify[i]['inequal'])
aggClassEst += weakClassify[i]['alpha'] * classEst
print aggClassEst
return sign(aggClassEst)
if __name__ == '__main__':
datMat, classLabels = loadSimpleData()
weakClassArr = adaBoostTrain(datMat, classLabels, 30)
print "weakClassArr:", weakClassArr
#test
result = adaBoostClassify([1, 1], weakClassArr)
print result
weakClassArr: [{'threshold': 1.3, 'dim': 0, 'inequal': 'left', 'alpha': 0.6931471805599453}, {'threshold': 1.0, 'dim': 1, 'inequal': 'left', 'alpha': 0.9729550745276565}, {'threshold': 0.90000000000000002, 'dim': 0, 'inequal': 'left', 'alpha': 0.8958797346140273}]
参考
1、机器学习实战
2、A Short Introduction to Boosting