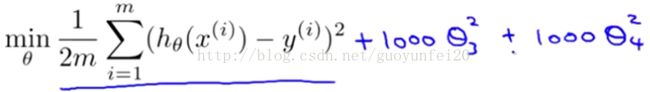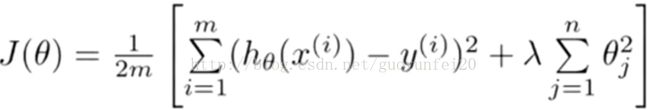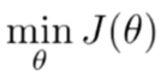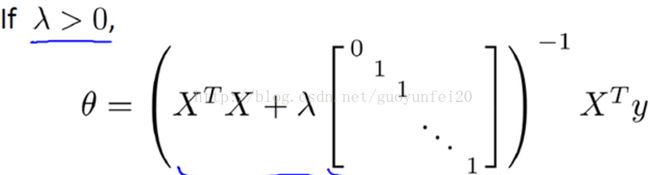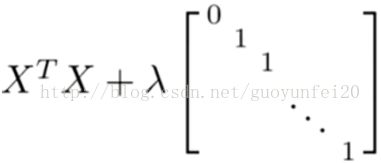正则化（regularization）
一、过拟合（overfitting）问题
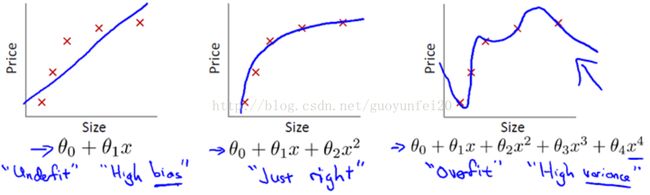
上图是房价（Price）与房子面积（Size）的关系的实例。我们的目标是利用多项式回归来根据房子面积来预测房价。
左边的模型仅用了一次项，此时模型参数有俩θ0、θ1，是一条直线；直观的观察样本点（红色×）的趋势，我们发现该模型并不能很好的拟合两者的关系（很明显，随着房子面积增大，住房价格的变化趋于稳定或者说越往右越平缓）。此类情况称为欠拟合（underfitting）！
右边的模型用到了四次项，此时模型参数由五个θ0、θ1、θ2、θ3，θ4，此时从表面看上去模型很好的拟合了样本点；但实际上这是一条非常扭曲的曲线，它不停的上下波动。当一个新的样本（Size）需要预测时，结果也不准确！这类情况叫做过拟合（overfitting）！
只有中间的模型，参数不多不少，刚好能反应Size和Price之间的真实关系！
二、利用正则化来解决过拟合问题
首先应当知道：
1、特征数量过多（对应上例中就是多项式项数过多，即θ参数数量过多）；
2、训练样本过少
都会导致过拟合的问题。因此，对应的，可以从两个方面下手来解决过拟合的问题：
1、减少特征数量（reduce number of features）
2、增加样本数量，或样本增强
但有时我们的样本数量有限，同时我们也不想减少特征数量（因为可能每个特征都会对结果一些贡献），该怎么办呢？
答案就是——用正则化！
正则化就是在特征数量不变的情况下，减少某些θ参数的值，使其对预测结果（y，上例中就是Price）的贡献较小！
对于上例右侧情况（过拟合的模型），正则化具体过程：
首先得知道训练模型就是最小化一个代价函数：
当上式最小时的参数θ值，就是我们要训练的模型参数了。
接下来，我们假设加上俩惩罚项，从而使θ3，θ4足够小。例如下边这样：
1000 只是我随便写的某个较大的数字而已。这样我们最小化加了惩罚项的代价函数时，θ3，θ4就非常小，接近于0；这样模型就和上例中间的模型差不多了！这就是正则化的效果！
严谨一些的话，正则化就是在代价函数中加入惩罚项：
然后最小化代价函数就可以了：
其中：
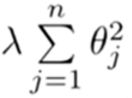就是正则项！λ成之为正则化参数，用来控制平衡。当λ非常大时，会把使所有的参数非常小！这样模型也是不行的。
三、线性回归中的正则化
对于线性回归，我们知道其最小二乘解：（推导过程略）
如果加入了正则项后：
其最小二乘解为：（推导过程略）
现在考虑 M（即样本量）， 比 N（即特征的数量）小或等于N的情况：
根据线性代数理论，如果有效方程数小于未知数时，方程有无穷多个解的。对应于模型就是说无法确定单一θ值！但加入了正则项后，只有λ > 0，不难证明
是可逆的，同时保证了唯一解！
二、举例（TensorFlow中Full Connection中加入正则化。代码仅是示例，不保证能运行）：
#coding:utf-8
import tensorflow as tf
def get_weight(shape, lambda):
var = tf.Variable(tf.random_normal(shape), dtype=tf.float32)
# 把正则化加入集合losses里面
tf.add_to_collection("losses",tf.contrib.layers.l2_regularizer(lambda)(var))
return var
x = tf.placeholder(tf.float32,shape=(None, 2))
y_= tf.placeholder(tf.float32,shape=(None, 1)) # ground true
# 神经网络层节点的个数
layer_dimension = [2,10,10,10,1]
# 神经网络的层数
n_layers = len(layer_dimension)
cur_layer = x
in_dimension = layer_dimension[0]
for i in range (1, n_layers):
out_dimension = layer_dimension[i]
weight = get_weight([in_dimension,out_dimension], 0.001)
bias = tf.Variable(tf.constant(0.1, shape(out_dimension)))
cur_layer = tf.nn.relu(tf.matmul(x, weight)) + bias)
in_dimension = layer_dimension[i]
# 计算最终输出与标准之间的loss
ses_loss = tf.reduce_mean(tf.square(y_ - cur_layer))
# 把均方误差也加入到集合里
tf.add_to_collenction("losses", ses_loss)
# tf.get_collection返回一个列表,内容是这个集合的所有元素
# add_n()把输入按照元素相加
loss = tf.add_n(tf.get_collection("losses"))