Trie树的构建和应用

Trie树又叫“字典树”，是一种在字符串计算中极为常见的数据结构。在介绍Trie树的具体结构之前，我们首先要搞明白的就是Trie树究竟是用来解决哪一类问题的，为什么这类问题可以用Trie树高效的解决。

我们为什么用Trie树

1. 节约字符串的存储空间

假设现在我们需要对海量字符串构建字典。所谓字典就是一个集合，这个集合包含了所有不重复的字符串，字典在对文本数据做信息检索系统时的作用我想毋庸赘述了。那么现在就出现了一个问题，那就是字典对存储空间的消耗过大。而当这些字符串中存在大量的串拥有重复的前缀时，这种消耗就显得过于浪费了。比如: "ababc","ababd","ababrf","abab...",... ，这些字符串几乎都拥有公共前缀”abab”。 我们直接的想法是，能不能通过一种存储结构节约存储成本，使得所有拥有重复前缀的串对于公共前缀只存储一遍。这种存储的应用场景如果是对DNA序列的存储，那么出现重复前缀的可能性更大，空间需求也就更为强烈。

2. 字符串检索

检索一个字符串是否属于某个词典时，我们当前一般有两种思路：

• 线性遍历词典，计算复杂度 O(n) ， n 为词典长度；
• 利用hash表，预先处理字符串集合。这样再搜索运算时，计算复杂度 O(1) 。但是hash计算可能存在碰撞问题，一般的解决办法比如对某个hash值所代表的字符串实施二次检索，则计算时间也会上来。而且，hash虽说是一种高效算法，其计算效率比直接字符匹配还是要略高的。

所以，能不能设计一种高效的数据结构帮助解决字符串检索的问题？

3. 字符串公共前缀问题

这里有两个非常典型的例子：

• 求取已知的 n 个字符串的最长公共前缀，朴素方法的时间复杂度为 O(nt) ， t 为最长公共前缀的长度；
• 给定字符串 a ，求取 a 在某 n 个字符串中和哪些串拥有公共前缀

对于问题(2)，除了朴素的比较法之外，我们还可以采取对每个字符串的所有前缀计算hash值的方法，这样一来，计算所有前缀hash值复杂度 O(n∗len) ， len 为字符串的平均长度，查询的复杂度为 O(n) 。虽然降低了查询复杂度，但是计算hash值显然费时费力。

Trie树的构造

1. 结构

Trie树是如图所示的一棵多叉树。其中存储的字符串集合为:
{"a","aa","ab","ac","aab","aac","bc","bd","bca","bcc"}

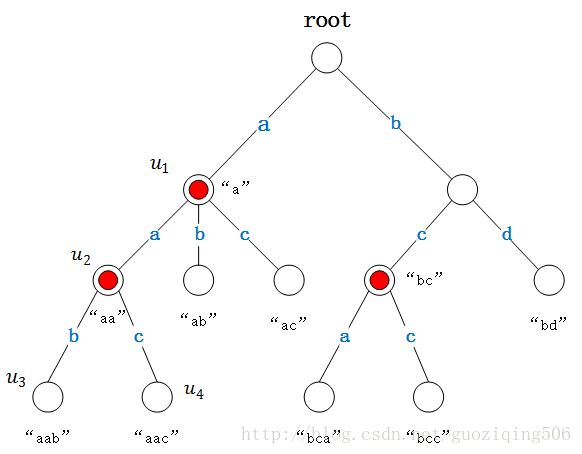
从上图我们可以看出，Trie树有如下3点特征：

• 根节点不代表字符，除根节点外每一个节点都只代表一个字符（一般的解释是，是除根节点外所有节点只“包含”一个字符，我在这里说“代表”，而不说“包含”是因为后面的算法设计中，为了使Trie树的结构更加清晰，我并没有让任何节点“包含”字符）。
• 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
• 每个节点的所有子节点包含的字符都不相同。

其实，一棵完整的Trie树应该每个非叶节点都拥有26个指针，正好对应着英文的26个字母，这样整棵树的空间成本为 26l ， l 为最长字符串的长度。但是为了节省空间，我们可以根据字符串集本身为每个非叶节点，“量身定做”子节点。以上面的图为例，以”a”开头的字符串中，第二个字符只有”a, b, c”3种可能，我们当然没有必要为节点 u1 生成26个子节点了，3个就够了。

除此之外，由于有些字符就是集合中其他字符的前缀，为了能够分辨清楚集合中到底有哪些字符串，我们还需要为每个节点赋予一个判断终止与否的bool值，记为 end 。比如上图，由于同时存在字符串 {"a","ab","ac","aa","aab","aac"} ，我们就令节点 u1,u2 的 end值为True，表示从根节点到 u1,u2 的路径上的字符按顺序可以构成集合中一个完整的字符串（如”a”, “aa”）。图中，我们将end == True的节点标红。

2. 构建Trie树

理解了上面Trie树的结构，就可以放手去写代码了，实现起来其实非常简单，几乎没有任何难度，需要注意的是我们究竟以一种什么样的形式来定义节点。这一点其实每个人的想法还是有些区别的，我是这般定义：

class TrieTreeNode(object):
    def __init__(self):
        self.end = False

        # The labels of pointers in the node
        self.pointerLabels = []

        # The pointers
        self.pointers = []

除了end之外，还有两个list型的变量，pointerLabels和pointers，前者表示的是此节点的所有指针的标签，标签表示其实才是字符，如上图每个指针上面的字符，而pointers代表的是此节点的每个孩子节点的地址。这样设计的好处在于，查询时我们能够直接根据当前节点包含的数据判断一下个字符否存在，该往那条路径继续遍历，而不是依次访问当前节点的所有孩子。而除了根节点之外的所有节点都“代表”着被指向的指针的标签。拿上图的节点 u2 来说，它的结构是这样的：

root.end = True
root.pointers = [u4, u5]
root.pointerLabels = ["b", "c"]

下面给出完整的构建Trie树的代码：

def buildTrieTree(stringList):
    """
    :param stringList: the collection of strings
    :return: 
    """

    root = TrieTreeNode()

    for ele in stringList:
        cur = root

        for char in ele:

            if char not in cur.pointerlabels:
                cur.pointerLabels.append(char)
                newNode = TrieTreeNode()
                cur.pointers.append(newNode)

                if char != ele[-1]:
                    cur = newNode

            # When char in cur.pointerlabels
            elif char != ele[-1]:
                pos = cur.pointerlabels.index(char)
                cur = cur.pointers[pos] 
            else:
                cur.end = True
    return root

3. 查询Trie树

给出在Trie树上查询某个字符串是否存在的代码，这个非常简单了，不多说了。

def trieTreeQuery(inputString, trieTreeRoot):
    """
    :param inputString: the string that need to be searched
    :param trieTreeRoot: the root of Trie tree
    :return: 
    """
    cur = trieTreeRoot
    for char in inputString:
        if char not in cur.pointerlabels:
            return False
        else:
            pos = cur.pointerlabels.index(char)
            cur = cur.pointers[pos]
    if cur.end is True:
        return True
    return False

性能分析

从上面字符串检索的算法我们可以分析出，无论有多少字符串，我们检索一个字符串的时间为 O(m) ， m 为要检索的字符串的长度。若要查询一个已知串是否为字符串集合中某些字符串的前缀，也可以通过Trie树查找到相应的分支，将分支往下一直到叶子的所有路径找出，就是检索结果了，比如上图中，要查”aa”是否为前缀，我们当然是先遍历到节点 u2 ，然后再找出以 u2 为根的子树的所有叶子（ u4,u5 ），每条从root到这每个叶子的路径就构成了字符串。至于求取公共子串的问题，Trie树可以以复杂度 O(t) （ t 是最长公共前缀的长度）直接找到。这里就不给出具体算法了。