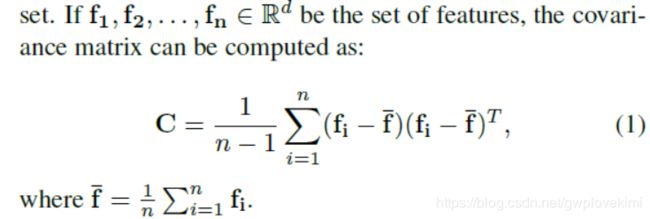学习笔记之——covariance pooling

《Covariance Pooling for Facial Expression Recognition》

代码：https://github.com/d-acharya/CovPoolFER

摘要

将面部表情分类为不同类别需要捕获面部关键点的区域扭曲（Classifying facial expressions into different categories requires capturing regional distortions of facial landmarks.）。我们认为，协方差等二阶统计量能够更好地捕捉区域​​面部特征中的这种扭曲。在这项工作中，我们探索了使用流形网络结构进行协方差合并以改善面部表情识别的好处。特别地，我们首先将这种类型的流形网络与传统的卷积网络结合使用，以便以端到端的深度学习方式在各个图像特征映射内进行空间汇集。通过这样做，我们能够在野外静态面部表情（SFEW 2.0）的验证集上实现58.14％的识别准确度，在真实世界情感面部（RAF）数据库1的验证集上实现87.0％的识别准确度。这些结果是我们所知的最佳结果。此外，我们利用协方差池来捕捉基于视频的面部表情识别的每帧特征的时间演变。我们报告的结果证明了通过在卷积网络层之上堆叠设计的协方差池的流形网络来暂时汇集图像集特征的优点

introduction

面部表情在传达我们的思想状态中起着重要的作用。人类和计算机算法都能从对面部表情进行分类中获益。自动面部表情识别的可能应用包括更好地转录视频、电影或广告推荐、远程医疗中的疼痛检测等。
传统的卷积神经网络(CNNs)使用卷积层、最大或平均池和全连通层，只捕获一阶统计量[25]。二阶统计量(如协方差)被认为是比一阶统计量(如平均或最大[20])更好的区域描述符。
 

如上图所示，面部表情识别更直接地与面部特征点的变形有关，而不是与特定特征点的存在与否有关。我们认为，二阶统计量比一阶统计量更适合捕捉这种扭曲。为了深入学习二阶信息，我们引入最后一个卷积层后的协方差池化。为了进一步降维，我们从流形网络[11](manifold network)中借用概念，并与传统的CNNs一起进行端到端训练。需要指出的是，这并不是第一次将二阶池引入传统的CNNs。在[13]中，协方差池最初用于从CNNs的输出池化协方差矩阵。[25]提出了一种在CNNs环境下计算二阶统计量的方法。然而，这两项工作并没有使用降维层或非线性校正层进行二阶统计。在这篇论文中，我们提出了在人脸表情识别的背景下探索它们的强烈动机。
本文的贡献是两方面的
1、视频和图像在人脸表情识别上下文中的二阶统计量的端到端池化
2、基于图像的人脸表情识别的研究进展取得了State-of-art result

Facial Expression Recognition and Covariance Pooling

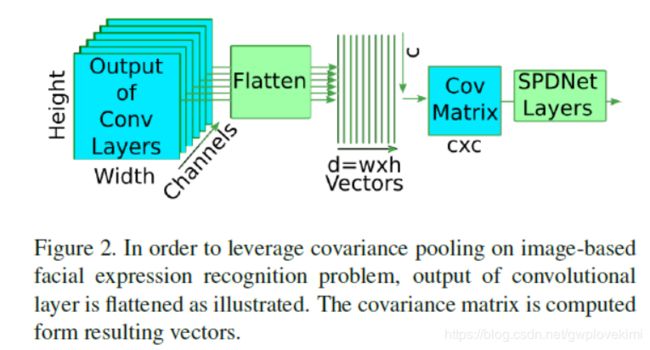
面部表情定位于面部区域，而野外图像包含大量的无关信息。因此，首先进行人脸检测，然后根据人脸地标位置进行对齐。接下来，我们将标准化的面孔输入一个深度CNN。To pool the feature maps spatially from the CNN,我们提出使用covaraince池，然后利用流形网络[11]深入学习这些二阶统计量。我们提出的基于图像的人脸表情识别模型的流程如图2所示。

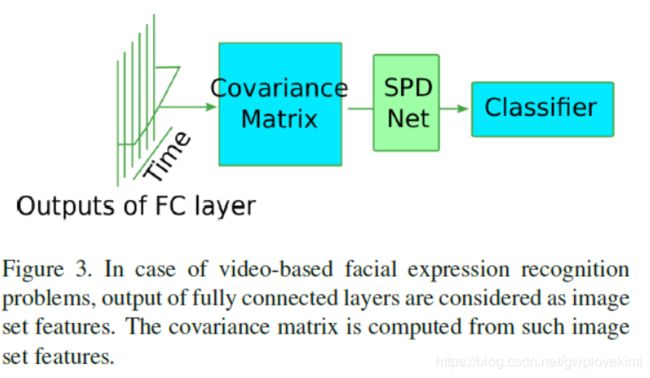
作为基于图像的面部表情识别的案例,在野外的视频包含了大量无关的信息。首先,所有的帧都是从视频中提取出来的。然后在每个帧上执行人脸检测和对齐。根据特征提取算法的不同，要么从归一化人脸中提取图像特征，要么将归一化人脸进行拼接，并对拼接后的帧进行三维卷积。直观地说,随着时间的方差可以捕捉到有用的面部运动模式,我们建议将帧与时间相结合。为了深入了解时空二阶信息,我们还采用了流型网络[11]对协方差矩阵的维数减少和非线性。图3给出了基于视频的面部表情识别模型的概述。
 

因此，这两种模型的核心技术是空间/时间协方差池和用于深入学习二阶特征的流形网络。下面我们将介绍两个关键技术

Covariance Pooling

如前所述，由全连接层、最大或平均池化层和卷积层组成的传统cnn只捕获一阶信息[25]。ReLU引入了非线性，但只在单个像素级引入。由特征计算的协方差矩阵被认为比一阶统计量[20]更能捕捉区域特征。、

在给定一组特征的情况下，协方差矩阵可以用来简洁地概括该集合中的二阶信息

所得到的矩阵是对称正定的(SPD)，仅当{f1, f2，…，f n}大于d，为了利用SPD流形网络[11]的几何结构保持层，需要协方差矩阵为SPD。然而，即使矩阵只是正半定的，也可以通过向协方差矩阵的对角线元素添加多个trace来正则化:

Covariance Matrix for Spatial Pooling

为了将协方差池应用于基于图像的人脸表情识别问题，如图2所示，可以将最终卷积层的输出进行摊平，并用于计算协方差矩阵
令X∈R w×h×d为经过几个卷积层后得到的输出，其中w,h,d
分别表示输出中的宽度、高度和通道数。X可以被展平为元素X '∈R n×d，其中n = w×h。，f n∈R d为X '的列，我们可以像Eqn 1那样通过计算协方差来捕捉信道间的变化，并利用Eqn 2对计算矩阵进行正则化。
 

'''
implementation of covariance pooling layers
'''
def _cal_cov_pooling(features):
    shape_f = features.get_shape().as_list()
    centers_batch = tf.reduce_mean(tf.transpose(features, [0, 2, 1]),2)
    centers_batch = tf.reshape(centers_batch, [shape_f[0], 1, shape_f[2]])
    centers_batch = tf.tile(centers_batch, [1, shape_f[1], 1])
    tmp = tf.subtract(features, centers_batch)
    tmp_t = tf.transpose(tmp, [0, 2, 1])
    features_t = 1/tf.cast((shape_f[1]-1),tf.float32)*tf.matmul(tmp_t, tmp)
    trace_t = tf.trace(features_t)
    trace_t = tf.reshape(trace_t, [shape_f[0], 1])
    trace_t = tf.tile(trace_t, [1, shape_f[2]])
    trace_t = 0.0001*tf.matrix_diag(trace_t)
    return tf.add(features_t,trace_t)

 

 

参考资料：https://blog.csdn.net/heruili/article/details/88322472