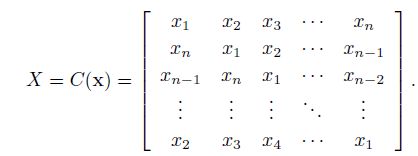目标跟踪算法学习笔记之一：KCF

版权声明：本文为博主原创文章，转载请注明出处。

简述

　　KCF（High-speed tracking with kernelized correlation filters）算法已经算是一篇非常经典的文章了，而且也被各路大神分析得很详尽了。我打算写这篇分析有两个原因：
1.相关滤波器CF（correlation filter）值得学习，值得深入探讨，可以被实际工程所用。
2.我想做个总结，主要想把相关滤波器有关的算法理一下。
好，废话不多说，下面开始，部分内容参考几位博主的文章和作者主页，如下：

http://blog.csdn.net/shenxiaolu1984/article/details/50905283
KCF高速跟踪详解：
http://blog.csdn.net/mhz9123/article/details/51670802
论文作者主页：
http://www.robots.ox.ac.uk/~joao/#

算法描述

　　算法把跟踪问题抽象为一个线性回归模型的求解，设代表目标图像的输入为z，权重w,输出为 f(w)=wTx ,目的就是找到f,能够最小化样本 xi 经分类器模型输出 f(xi) 和期望回归值 yi 的最小均方差的解:

minw∑(f(xi)−yi))2+λ∥w∥2(1)

其中 λ 是防过拟合的正则化参数。论文描述上述问题的解

w=(XHX+λI)−1XHy(2)

其中 XH=(X∗)T ，*表示复共轭，T表示转置，X的每一行是 xi ,上述解的推导有兴趣的可以去了解下。由于该式子不易求解，运算复杂是O(n^2),故作者采用了一个巧妙方法——循环矩阵。

循环矩阵

　　先给出循环矩阵的作用：根据循环矩阵能够被离散傅里叶矩阵对角化，使得矩阵求逆转换为特征值求逆的性质；能够将问题(2)转换到频域进行运算，应用离散傅里叶变换(DFT)提高运算速度，然后再将解逆变换回空域从而得到响应最大的解 ymax 。
这就是本算法的最重要的地方，我们也可以类比MOSSE算法中的相关滤波器的作用，两者是相通的。
循环矩阵X的构造是每一行由基样本(base sample)x的循环偏移向量组成，如下：

如果用图像形象化描述就是

中间的基样本图像分别左移和右移得到其余的样本，而且循环矩阵所具备的性质正是帮助对式2求解的关键： 1.循环矩阵C(x)可以被DFT矩阵F对角化：

X=Fdiag(x^)FH(3)

其中 x^ 是 x 的傅里叶变换， F 是离散傅里叶矩阵。 DFT矩阵：

F=1K−−√⎡⎣⎢⎢⎢⎢11111ww2w31w2w4w61w3w6w9⎤⎦⎥⎥⎥⎥,w=e−2πi/K(4)

DFT矩阵的性质： -对称矩阵 -满足 FFH=FHF=I 我们可以用matlab试验上述性质：

%1 diagnolize 对角化
K=5; %dimension of problem
x_base=rand(1,K); %generator vector
X=zeros(K,K);         %circulant matrix

for k=1:K
    X(k,:)=circshift(x_base,[0 k-1]);
end
x_hat=fft(x_base);  %DFT
F=transpose(dftmtx(K))/sqrt(K); %转置 得到DFT matrix
X2=F*diag(x_hat)*F'; %"‘"指转置共轭，对应于T
display(X);
display(real(X2));%X=X2 验证X=F*diag(x_hat)*F'性质

因此循环矩阵的作用是：将矩阵求逆变换为特征值求逆，从而提高运算速度。

关键公式推导

根据公式2先求 XXH ：

XH=(X∗)T=(F∗diag(x^∗)FH∗)T=(FHdiag(x^∗)F)T=Fdiag(x^∗)FH(5)

这里的圆圈符号，相当于矩阵点乘运算。之后对公式2进行展开：

w=(XX+λI)−1XHy=(Fdiag(x^∗⨀x^)FH+Fdiag(λ)FH)−1XHy=(Fdiag(x^∗⨀x^+λ)FH)−1XHy=(Fdiag(x^∗x^∗⨀x^+λ)FH)y(6)

利用反对角化性质： Fdiag(y)FH=C(F−1(y)) 得到：

w=C(F−1(x^∗x^∗⨀x^+λ))y(7)

再利用循环矩阵卷积性质: F(C(x)y)=F∗(x)⨀F(y) 得到：

F(w)=F(C(x)y)=(x^∗x^∗⨀x^+λ)∗⨀F(y)=x^⨀y^x^∗⨀x^+λ(8)

论文中的分子部分是错误的，但是代码中还是正确的。
这里就是本文的核心，而据此我们可以通过上式逆傅里叶变换得到线性回归系数w。

核化技巧

　　上述仅是线性问题的求解，作者在文中进行了非线性问题的解的拓展，即引入了核来将问题扩展到非线性空间。核技巧在SVM中应用最广，这里不具体展开，有不少博客和书籍写得不错。
上述问题的回归系数 w 用x和对偶空间 α 的线性组合表示如下：

w=∑iαiψ(xi)

回归问题就转为：

f(z)=wTz=∑i=1nαiψ(xi)ψ(zi)=∑i=1nαiκ(z,xi)(9)

其中 κ(z,xi)=ψ(z)ψ(xi) 就是核函数，常用的有高斯核、多项式核和线性核，本文中默认用的是高斯核。故将求回归系数 w 转化为求 α 。
根据文献8，我们可以得到非线性问题的解：

α=(K+λI)−1y

这里根据文中的定理1结合之前 w 的推导，可以得到

α^=y^k^xx+λ(10)

其中 kxx 是核矩阵 K=C(kxx) 的第一行。
这样对于输入z，同样构造矩阵 Kz=C(kxz),kxz 就是 x 和 z 的核相关,据此我们可以对所有的pathch进行回归检测：

f^(z)=k^xz⨀α^(11)

将响应值 f^(z) 逆变换回空域，找到最大值对应的patch既是结果。至于如何进行核相关，参见文中第6小节所述。

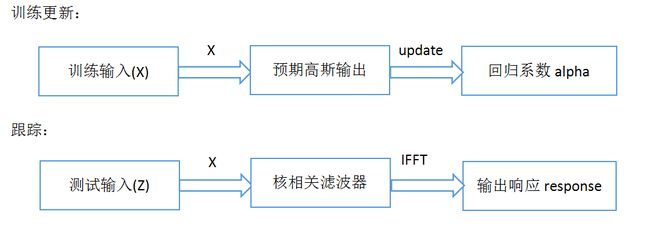
运行流程

根据上述的理论分析，我们可以给出KCF算法的pipeline：

总结

　　KCF算法是近年来相当流行和高速的跟踪算法，其与相关滤波器也有这本质上的联系，非常值得学习，这篇算法很大一部分都是拾人牙慧，不过是想用自己的思路再梳理一边，感谢其他博主的贡献。在下篇DSST算法中，我将对两者的细节之处进行对比，其实作者也在文中末尾提到了两者的区别，但是还想说几句。学习了一阵算法后愈发觉得数学的重要性，这些简洁和神奇的idea着实令人惊奇和着迷。