深度学习中的结构化概率模型
深度学习中的结构化概率模型
结构化概率模型也称为图模型。
一,非结构化建模的挑战
概率模型可以完成很多任务,例如:
- 估计密度函数
- 去噪
- 缺失值的填补
- 采样
对上千甚至上百万的随机变量的分布建模,无论从计算上还是统计意义上来说,都是一个极具挑战性的任务。
非结构化建模的主要挑战在于参数的数量是巨大的,这会导致:
- 内存:存储参数的开销太大。
- 统计的高效性:容易过拟合,因为数据量不够,所以需要一些平滑方法。
- 推断的时间太长:例如利用联合分布求一些边缘分布或者条件分布。
- 采样的时间太长
主要问题在于我们显示地对每一种可能的变量子集所产生的每一种可能类型的相互作用进行了建模!而实际问题中我们遇到的概率分布远比这个要简单,实际中很多变量只是间接地相互作用,而这种间接地相互作用是可以忽略的,真正需要建模的只是随机变量之间的直接作用!
而结构化概率模型为随机变量之间的直接作用提供了一个正式的建模框架。这种方式大大减少了模型的参数个数,以至于只需要更少的数据来进行有效的估计。这些更小的模型大大减小了在模型存储、模型推断以及从模型中采样时的计算开销。总之,使用结构化概率模型的主要优点是,它们能显著降低表示概率分布、学习和推断的成本。
二,使用图描述模型结构
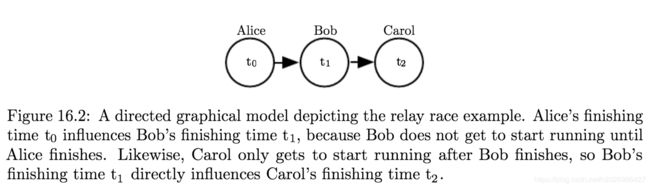
有向模型
有向图模型是一种结构化概率图模型,也被称为信念网络或者贝叶斯网络。例如:
无向模型
无向图模型是另一种结构化概率图模型,也被称为马尔可夫随机场或者马尔可夫网络。
然而并不是所有情况的相互作用都有一个明确的方向关系。当相互作用并没有本质性的指向,或者是明确的双向相互作用时,使用无向模型更加合适。
配分函数
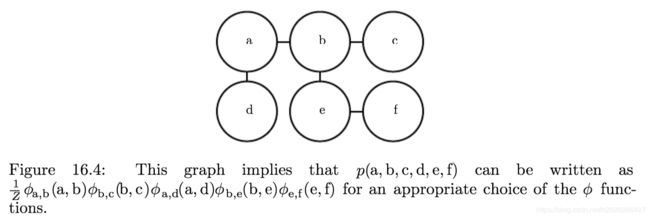
无向图联合概率的计算方法如下:
其中,Z是归一化常数,或者称为配分函数。它通常是由对所有可能的x状态的联合分布空间求和或者积分得到,所以一般很难计算,因此需要使用一些近似方法来计算。
有向模型和无向模型之间一个重要的区别就是有向模型是通过起始点的概率分布直接定义的,反之无向模型的定义显得更加宽松,通过 ϕ \phi ϕ函数转化为概率分布而定义。这改变了我们处理这些建模问题的直觉。当我们处理无向模型时,需要牢记一点,每一个变量的定义域对于一系列给定的 ϕ \phi ϕ函数所对应的概率分布有着重要的影响!
例如:
如果 x ∈ { 0 , 1 } n x\in \{0,1\}^n x∈{0,1}n,那么 p ( x ) p(x) p(x)可以被分解成n个独立的分布,并且满足 p ( x i = 1 ) = s i g m o i d ( b i ) p(x_i=1)=sigmoid(b_i) p(xi=1)=sigmoid(bi);
如果x的定义域是基本单位向量的集合{[1,0,…,0],[0,1,…0],…,[0,0,…,1]},那么 p ( x ) = s o f t m a x ( b ) p(x)=softmax(b) p(x)=softmax(b)。
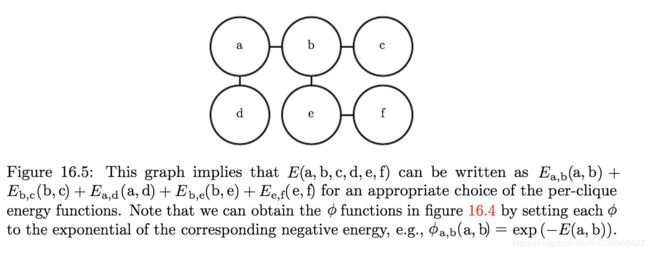
基于能量的模型
p ^ ( x ) = exp ( − E ( x ) ) \hat p(x)= \exp(-E(x)) p^(x)=exp(−E(x))
其中 E ( x ) E(x) E(x)被称为能量函数,基于能量的模型使得我们在学习能量函数的过程中,可以使用无约束的优化方法。
服从上式的任意分布都是玻尔兹曼分布的一个实例,所以我们把许多基于能量的模型称为玻尔兹曼机。
虽然玻尔兹曼机最初的定义既可以包含潜变量,又可以不包含潜变量,但时至今日玻尔兹曼机这个术语通常用于指拥有潜变量的模型,而没有潜变量的玻尔兹曼机则经常称为马尔可夫随机场或对数线性模型。
实际上对概率模型进行操作的算法并不需要计算 p m o d e l ( x ) p_{model}(x) pmodel(x),只需要计算 log p m o d e l ( x ) \log{p_{model}(x)} logpmodel(x)。对于具有潜变量h的基于能量的模型,这些算法有时会将该量的负数称为自由能:
F ( x ) = − log ∑ h exp ( − E ( x , h ) ) F(x)=-\log{\sum_h\exp(-E(x,h))} F(x)=−logh∑exp(−E(x,h))
因子图
因子图是从无向模型中抽样的另一种方法,它可以解决标准无向模型语法中表达的模糊性。例如:
三,从图模型中采样
图模型同样简化了从模型中采样的过程。
原始采样
- 定义:将有向图模型中的变量按照拓扑排序,依次进行采样即可。
- 优点:采样速度非常快,而且非常方便。
- 缺点:仅适用于有向图模型,而且并不是每次采样都是条件采样操作。
Gibbs采样
从无向模型中抽取样本是一个成本很高的多次迭代的过程,理论上最简单的方法是Gibbs采样。
- 具体过程:在一个n维向量的随机变量x上有一个图模型,我们迭代地访问每一个变量 x i x_i xi,在给定其他变量的条件下从 p ( x i ∣ x − i ) p(x_i|x_{-i}) p(xi∣x−i)中采样。由于图模型的分离性质,在抽取 x i x_i xi时我们可以等价地仅对 x i x_i xi的邻居条件化。
- 优点:适用于任何图模型。
- 缺点:不幸的是,在我们遍历图模型一次并采样所有n个变量之后,我们仍然无法得到一个 p ( x ) p(x) p(x)的客观样本。相反,我们必须重复该过程并使用它们邻居的更新值对所有的n个变量重新采样。在多次重复之后,该过程才渐进地收敛到正确的目标分布。所以我们很难确定样本何时到达所期望分布的的足够精确的近似,而且这样采样出的样本之间是有一定的相关性的,并不是完全随机的。
四,推断和近似推断
很多方法通过学习潜变量来完成特征学习,通常给定v和h,实验结果显示 E [ h ∣ v ] E[h|v] E[h∣v]和 a r g m a x h p ( h , v ) argmax_hp(h,v) argmaxhp(h,v)都是v的良好的特征映射。
给定一组医学测试,我们可以推断患者可能患什么疾病。在一个潜变量的模型中,我们可能需要提供能够描述可观察变量v的特征 E [ h ∣ x ] E[h|x] E[h∣x],一般使用MLE来训练我们的模型。由于
log p ( v ) = E h ∼ p ( h ∣ v ) [ log p ( h , v ) − log p ( h ∣ v ) ] \log p(v)=E_{h\sim p(h|v)}[\log p(h,v)-\log p(h|v)] logp(v)=Eh∼p(h∣v)[logp(h,v)−logp(h∣v)]
学习过程中,我们经常需要计算 p ( h ∣ v ) p(h|v) p(h∣v),而这就属于推断问题。
但由于直接计算 p ( h ∣ v ) p(h|v) p(h∣v)是及其复杂的,这就促使我们使用近似推断。在深度学习中,这通常涉及变分推断,其中通过寻求尽可能接近真实分布的近似分布 q ( h ∣ v ) q(h|v) q(h∣v)来逼近真实分布 p ( h ∣ v ) p(h|v) p(h∣v)。
五,结构化概率模型的深度学习方法
深度图模型的特点如下:
- 深度模型通常具有比可观察变量更多的潜变量,变量之间的非线性相互作用是通过多个潜变量的间接连接来实现的。而传统模型大多使用高阶项和结构学习来捕捉变量之间的非线性相互作用。如果有潜变量,则它们的数量通常很少。
- 深度图模型中的潜变量事先不包含什么特殊的含义,而传统图模型中的潜变量一般事先指定其特殊的含义,例如文档的主题、学生的智力或患者可能患的疾病等。
- 深度图模型使用矩阵参数化层之间的高效相互作用。
- 深度图模型可以设计来加速Gibbs采样或变分推断。
- 深度图模型有对未知量的较高容忍度。
实例:受限玻尔兹曼机
受限的意思是RBM中在任何两个可见单元之间或者任何两个隐藏单元之间没有直接的相互作用。
详见深度学习的 P 356 P_{356} P356,解释得十分清晰!