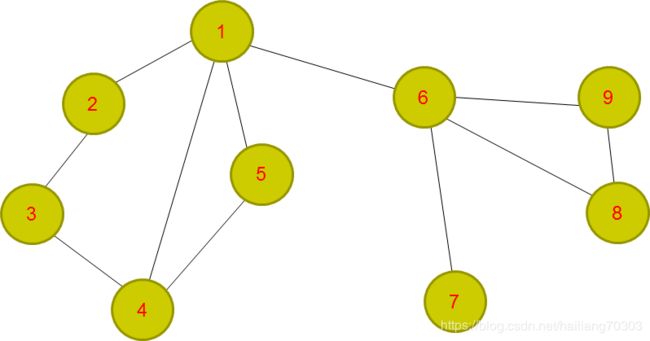
寒假2019培训：双连通分量（点双+边双）

定义：

若一个无向连通图不存在割点，则称它为“点双连通图”。若一个无向连通图不存在割边，则称它为“边双连通图”。
无向图的极大点双连通子图称为“点双连通分量”，简记为“v-DCC”。无向连通图的极大边双连通子图被称为“边双连通分量”，简记为“e-DCC”。二者统称为“双连通分量”，简记为“DCC”。

---

边双联通分量

求法：

核心概念： 没有割边
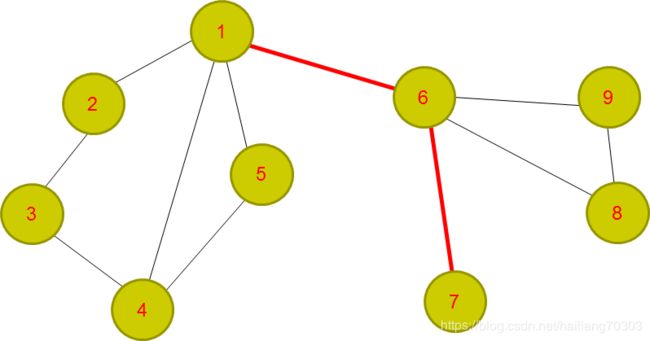
割边只会把图分成两部分，对图中的点没有影响。

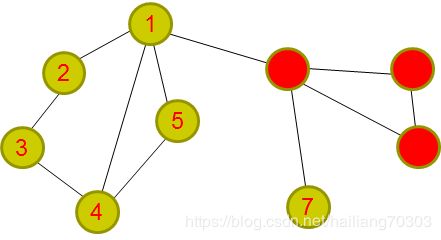
用红色临摹出来的，便是割边（请看我的另一个博客了解割边）
Tarjan学习+割点+割边+强连通分量

删除他们

上面就有三个边双了~~

算法：只需求出无向图中所有的割边，把割边都删除后，无向图会分成若干个连通块，每一个连通块就是一个“边双连通分量”。
具体实现：一般先用Tarjan算法求出所有的桥，然后再对整个无向图执行一次dfs遍历（遍历的过程不访问割边），划分出每个连通块即可。

贴上代码~

void dfs(int x){
    color[x] = tot;
    for(int i = linkk[x];i;i = e[i].n)
       if(!color[e[i].y] && !e[i].flag) //e[i].flag表示i为割边
          dfs(e[i].y);
}
void make_node(){
    t = 0;
    memset(linkk,0,sizeof(linkk));
    for(int i = 1;i <= m;++i){
        int j = i * 2; 
        int x = e[j].x , y = e[j].y;
        if(color[x] != color[y]) 
           insert( color[x] , color[y] ) ;
     }
    return;
}
// 主程序
 for(int i = 1;i <= n;++i)
      if(!color[i]) ++tot , dfs(i);
    make_node();

上一道模板题吧

bzoj 1718: [Usaco2006 Jan] Redundant Paths 分离的路径

题目描述
In order to get from one of the F (1 <= F <= 5,000) grazing fields (which are numbered 1…F) to another field, Bessie and the rest of the herd are forced to cross near the Tree of Rotten Apples. The cows are now tired of often being forced to take a particular path and want to build some new paths so that they will always have a choice of at least two separate routes between any pair of fields. They currently have at least one route between each pair of fields and want to have at least two. Of course, they can only travel on Official Paths when they move from one field to another. Given a description of the current set of R (F-1 <= R <= 10,000) paths that each connect exactly two different fields, determine the minimum number of new paths (each of which connects exactly two fields) that must be built so that there are at least two separate routes between any pair of fields. Routes are considered separate if they use none of the same paths, even if they visit the same intermediate field along the way. There might already be more than one paths between the same pair of fields, and you may also build a new path that connects the same fields as some other path.

为了从F(1≤F≤5000)个草场中的一个走到另一个，贝茜和她的同伴们有时不得不路过一些她们讨厌的可怕的树．奶牛们已经厌倦了被迫走某一条路，所以她们想建一些新路，使每一对草场之间都会至少有两条相互分离的路径，这样她们就有多一些选择． 每对草场之间已经有至少一条路径．给出所有R(F-1≤R≤10000)条双向路的描述，每条路连接了两个不同的草场，请计算最少的新建道路的数量, 路径由若干道路首尾相连而成．两条路径相互分离，是指两条路径没有一条重合的道路．但是，两条分离的路径上可以有一些相同的草场． 对于同一对草场之间，可能已经有两条不同的道路，你也可以在它们之间再建一条道路，作为另一条不同的道路．

输入格式
Line 1: Two space-separated integers: F and R * Lines 2…R+1: Each line contains two space-separated integers which are the fields at the endpoints of some path.

第1行输入F和R，接下来R行，每行输入两个整数，表示两个草场，它们之间有一条道路．

输出格式
Line 1: A single integer that is the number of new paths that must be built.

最少的需要新建的道路数．

样例数据
input

7 7
1 2
2 3
3 4
2 5
4 5
5 6
5 7
output

2
样例解释：

Building new paths from 1 to 6 and from 4 to 7 satisfies the conditions.
1 2 3
±–±--+
: | |
: | |
6 ±–±--+ 4
/ 5 :
/ :
/ :
7 + - - - -
Check some of the routes:
1 - 2: 1 -> 2 and 1 -> 6 -> 5 -> 2
1 - 4: 1 -> 2 -> 3 -> 4 and 1 -> 6 -> 5 -> 4
3 - 7: 3 -> 4 -> 7 and 3 -> 2 -> 5 -> 7
Every pair of fields is, in fact, connected by two routes.

It’s possible that adding some other path will also solve the problem
(like one from 6 to 7). Adding two paths, however, is the minimum.
数据规模与约定
时间限制：1s
空间限制：256MB

解析：

分析：在同一个边双连通分量中，任意两点都有至少两条独立路可达，所以同一个边双连通分量里的所有点可以看做同一个点。
缩点后，新图是一棵树，树的边就是原无向图的桥。
现在问题转化为：在树中至少添加多少条边能使图变为双连通图。
结论：添加边数=（树中度为1的节点数+1）/2
具体方法为，首先把两个最近公共祖先最远的两个叶节点之间连接一条边，这样可以把这两个点到祖先的路径上所有点收缩到一起，因为一个形成的环一定是双连通的。然后再找两个最近公共祖先最远的两个叶节点，这样一对一对找完，恰好是(leaf+1)/2次，把所有点收缩到了一起。
其实求边双连通分量和求强连通分量差不多，每次访问点的时候将其入栈，当low[u]==dfn[u]时就说明找到了一个连通的块，则栈内的所有点都属于同一个边双连通分量，因为无向图要见反向边，所以在求边双连通分量的时候，遇到反向边跳过就行了。
网上有一种错误的做法是:因为每一个双连通分量内的点low[]值都是相同的，则dfs()时，对于一条边(u,v),只需low[u]=min(low[u],low[v])，这样就不用缩点，最后求度数的时候，再对于每条边(u,v)判断low[u]是否等于low[v]，若low[u]!=low[v]，则不是同一个边双连通分量，度数+1即可…
咋看之下是正确的，但是这种做法只是考虑了每一个强连通分量重只有一个环的情况，如果有多个环，则会出错。
比如这组数据：
16 21
1 8
1 7
1 6
1 2
1 9
9 16
9 15
9 14
9 10
10 11
11 13
11 12
12 13
11 14
15 16
2 3
3 5
3 4
4 5
3 6
7 8
答案是1，上面错误的做法是0

点评：
边双连通分量缩点后，原图变成一颗真正的树，而树上各种操作可以和其他知识点结合起来。
这种敏感性要有，比如缩点之后就可以快速求必经边，必经点之类的

原装代码：

#include
using namespace std;
int n,m,k,len,tot,cnt,top,ans;
const int N=10005;
int dis[N],last[N*2],s[N],low[N],_stack[N],dfn[N],father[N],_color[N*2],vis[N*2];
struct ss
{
	int to,next,u;
}e[N*2];
void insert(int x,int y)
{
	e[++len].next=last[x];
	e[len].to=y;
	e[len].u=x;
	last[x]=len;
}
void tarjan(int x,int fa)
{
	int i=last[x];
	for(dfn[x]=low[x]=++tot,_stack[++cnt]=x,s[x]=1;i;i=e[i].next)
	{
		int v=e[i].to;
		if(father[i]==fa)continue;
		if(!dfn[v])
		{
			tarjan(v,father[i]);
			low[x]=min(low[x],low[v]);
		}
		else if(s[v])low[x]=min(dfn[v],low[x]);
	}
	if(low[x]>=dfn[x])
	{
	    ++top;
		int t=-1;
		do{
			t=_stack[cnt--];
			s[t]=0;
			_color[t]=top;
		}while(t!=x);
	}
}
int main()
{
	freopen("rpaths.in","r",stdin);
	freopen("rpaths.out","w",stdout);
	int i=0;
	for(scanf("%d%d",&n,&m);++i<=m;)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		insert(x,y);
		father[len]=++cnt;
		insert(y,x);
		father[len]=cnt;
	}
	for(cnt=0,i=0;++i<=n;)if(!dfn[i])tarjan(i,0);
	for(i=0;++i<=len;)
	{
		int x=e[i].u,v=e[i].to;
		if(_color[x]==_color[v])continue;
		++dis[_color[x]];
		++dis[_color[v]];
	}
	for(i=0;++i<=top;)
	 if(dis[i]==2)ans++;
	printf("%d",(ans+1)/2);
	
	
	return 0;
}

逃不掉的路

题目描述

现代社会，路是必不可少的。任意两个城镇都有路相连，而且往往不止一条。但有些路连年被各种XXOO，走着很不爽。按理说条条大路通罗马，大不了绕行其他路呗——可小撸却发现：从a城到b城不管怎么走，总有一些逃不掉的必经之路。

他想请你计算一下，a到b的所有路径中，有几条路是逃不掉的？

输入格式

第一行是n和m，用空格隔开。

接下来m行，每行两个整数x和y，用空格隔开，表示x城和y城之间有一条长为1的双向路。

第m+2行是q。接下来q行，每行两个整数a和b，用空格隔开，表示一次询问。

输出格式

对于每次询问，输出一个正整数，表示a城到b城必须经过几条路。

样例输入

5 5
1 2
1 3
2 4
3 4
4 5
2
1 4
2 5
样例输出

0
1
样例解释

第1次询问，1到4的路径有 1–2--4 ，还有 1–3--4 。没有逃不掉的道路，所以答案是0。
第2次询问，2到5的路径有 2–4--5 ，还有 2–1--3–4--5 。必须走“4–5”这条路，所以答案是1。

数据约定与范围

共10组数据，每组10分。

有3组数据，n ≤ 100 , n ≤ m ≤ 200 , q ≤ 100。
另有2组数据，n ≤ 10^ 3 , n ≤ m ≤ 2 x 10^ 3 , q ≤ 10^5。
另有3组数据，10^ 3 < n ≤ 10^ 5 ,m = n-1 , 100 < q ≤ 10^5。
另有2组数据，10^ 3 < n ≤ 10^ 5 , n ≤ m ≤ 2 x 10^ 5 , 100 < q ≤ 10^5。

对于全部的数据，1 ≤ x,y,a,b ≤ n；对于任意的道路，两端的城市编号之差不超过104；
任意两个城镇都有路径相连；同一条道路不会出现两次；道路的起终点不会相同;查询的两个城市不会相同。

题目简析：

既然是求必须经过的边，那么边双包含的集合肯定不是必须经过的，就可以把所有边双缩点。
原图得到一颗树后，问题就变成了简单的求树上两点之间的距离。
代码能力是必须要有的。

#include
#define N 100010
#define M 200010
using namespace std;
int n,m,q;
struct rode{
	int y,next,p;
}e[2*M]={},tr[M]={};
struct node{
	int x,y;
}e1[2*M]={};
int len=1,cnt=0,vs=0;
int dfn[N]={},low[N]={},fl[N]={},fh[N]={};
int f[N][30]={},d[N]={};
int col[N]={};
void inc(int x,int y){
	e[++len].y=y;
	e[len].next=fl[x];
	fl[x]=len;
}
void incc(int x,int y){
	tr[++len].y=y;
	tr[len].next=fh[x];
	fh[x]=len;
}
void tarjan(int u,int ff){
	dfn[u]=low[u]=++vs;
	for(int i=fl[u];i;i=e[i].next){
		int v=e[i].y;
		if(!dfn[v]){
			tarjan(v,i);
			low[u]=min(low[u],low[v]);
			if(dfn[u]q;
	q.push(1);d[1]=1;
	while(!q.empty()){
		int x=q.front();q.pop();
		for(int i=fh[x];i;i=tr[i].next){
			int y=tr[i].y;
			if(d[y])continue;
			d[y]=d[x]+1;
		    f[y][0]=x; 
			for(int j=1;j<=18;j++)
			 f[y][j]=f[f[y][j-1]][j-1];
			q.push(y);
		}
	}
}
int lca(int x,int y){
	if(d[y]=0;i--)
	 if(d[f[y][i]]>=d[x])y=f[y][i];
	if(x==y)return x;
	for(int i=18;i>=0;i--)
	 if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i];
	return f[x][0];
}
int main()
{
	freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);
	scanf("%d%d",&n,&m);int x,y;
	for(int i=1;i<=m;++i){
		scanf("%d%d",&x,&y);
		inc(x,y);inc(y,x);
		e1[i].x=x;e1[i].y=y;
	}
	tarjan(1,0);
	for(int i=1;i<=n;++i)
	 if(!col[i])++cnt,dfs(i);
	sd();
	bfs();
	scanf("%d",&q);
	for(int i=1;i<=q;++i){
		scanf("%d%d",&x,&y);int t=lca(col[x],col[y]);
		printf("%d\n",d[col[x]]+d[col[y]]-2*d[t]);
	}
	return 0; 
}

---

点双联通分量

无向连通图是“点双连通图”，当且仅当满足下列两个条件之一：
1）图的顶点不超过2个
2）图中任意两个点都同时包含在一个简单环中。“简单环”指的是不相交的环。
具体证明看算法进阶指南

性质

任意两点间至少存在两条点不重复的路径等价于图中删去任意一个点都不会改变图的连通性，即v-DCC中无割点
若v-DCC间有公共点，则公共点为原图的割点
无向连通图中割点一定属于至少两个v-DCC ，非割点只属于一个v-DCC

求法

还是原来的图


两个点双的图示，还有两个点双

然后的操作呢？？

就是创造树了~

自己画的可能会比较丑（总比老师半梦半醒的好 ）

点双连通分量的求法与边双连通分量的求法不一样。
割点可以包含在点双里。

点双连通分量的求法：
1）若某个点为“孤立点”，这个点肯定是点双。
2）其他的点双连通分量大小至少为2个点。
具体求法，还是看看我上一篇博客的tarjan强连通分量（链接前面已经给了）

与强联通分量类似，用一个栈来维护：
1、如果这个点第一次被访问时，把该节点进栈；
2、当割点判定法则中的条件 dfn[x]<=low[y]时，无论x是否为根，都要：
1）从栈顶不断弹出节点，直至节点y被弹出
2）刚才弹出的所有节点与节点x一起构成一个v-DCC。

void  tarjan (int x)
{
	 dfn[x]=low[x]=++num;
	 stack[++top]=x;
	 if (x==root  && linkk[x]==0) //孤立点
	 {
		 dcc[++cnt].push_back[x];
		 return;
	 }
	 int flag=0;
	 for (int i=linkk[x];i;i=e[i].next;) {	
		 int y=e[i].y;
		 if (!dfn[y]) { //y未访问过		 
			 tarjan(y);
			 low[x]=min(low[x],low[y]);
 if (low[y]>=dfn[x]) {//x对于y这个分支来说是割点			 
				 flag++;
				 if (x!=root || flag>1) cut[x]=true;
				 cnt++; int z;				 
				 do{
					  z=stack[top--];
					  dcc[cnt].push_back[z];
				   }while (z!=y) 
				dcc[cnt].push_back[x];	   
			 }
		 }// ！dfn[y] 结束
		 else low[x]=min(low[x],dfn[y]);		 
	 }	
}
//下面这些代码要放在主程序 tarjan后
for (int i=1;i<=cnt:i++)
{
	//第i个点双分支包含的点
	for (int j=0;j

例题来几道

【HDOJ3394】railway

题目描述
有一个公园有n个景点，这n个景点由m条无向道路连接而成。

公园的管理员准备规划一一些形成回路的参观路线(参观路线不能经过同一个景点，是一个简单环)。如果一条道路被多条参观路线公用，那么这条路是冲突的；如果一条道路没在任何一个回路内，那么这条路是多余的道路。

问分别有多少条有冲突的路和多余的路

输入格式
包括多组数据 每组数据第一行2个整数n，m

接下来m行，每行2个整数x，y，表示从x到y有一条无向边。

输入数据以n=0,m=0结尾

输出格式
一行2个整数，表示你要求的多余的道路和冲突的道路的数量。

样例数据
input

8 10
0 1
1 2
2 3
3 0
3 4
4 5
5 6
6 7
7 4
5 7
0 0
output

1 5
数据规模与约定
HDOJ 3394

0 < n <= 10000, 0 <= m <= 100000

时间限制：1s
空间限制：256MB

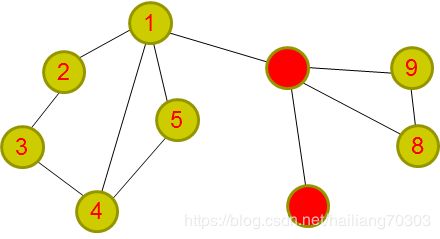
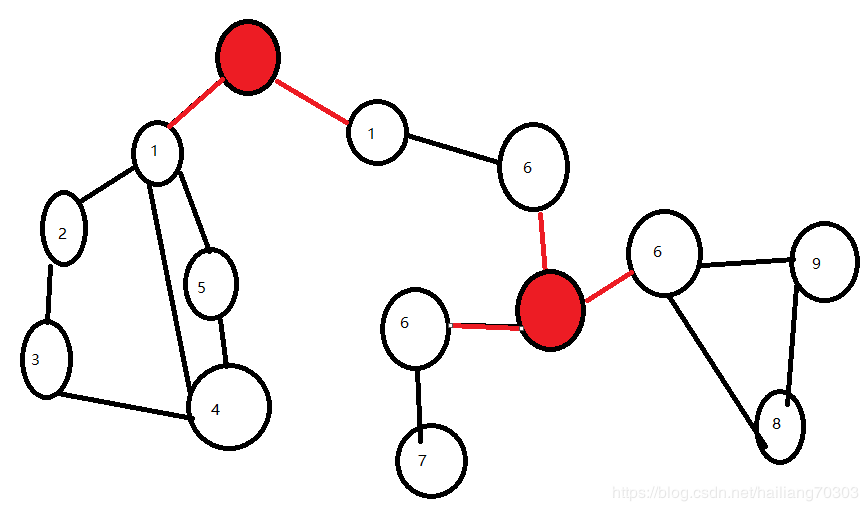
首先我们可以知道多余边就是该无向图中的桥,桥必然不在任何环中.冲突边只能在点双连通分量中？为什么不能是变双连通分量
很明显，一整个都是一个边双连通图，除此之外，这个边双还内置了两个割点、三个点双。但是需要计算的只是最左边的四个点

而什么样的点双连通分量有冲突边呢?

对于有n个节点和n条边(或小于n条边,比如2点1边)的点双连通分量,这种分量只有一个大环,不存在其他任何环了,所以这种分量中的边都不是冲突边.

对于有n个节点和m条边(m>n)的点双连通分量来说,该分量内的所有边都是冲突边.因为边数>点数,所以该分量必有至少两个环,我们随便画个图就可知其中的任意边都至少在两个以上的环上.
综上所述,对于多余边,我们输出桥数.对于冲突边,我们输出边数>点数的点双连通分量的所有边数.

上代码看看~

#include
using namespace std;
const int N=100005;
int n,m,k,ans1,ans2,len,cnt,top,tot;
int last[N],low[N],dfn[N],_stack[N],s[N];
bool vis[N];
struct ss
{
    int to,next;
}e[N*20];
void insert(int u,int v)
{
    e[len].to=v;
    e[len].next=last[u];
    last[u]=len++;
}

void work()
{
    tot=0;
    for(k=0;++k<=s[0];)
        for(int i=last[s[k]];i!=-1;i=e[i].next)
        {
            int v=e[i].to;
            if(vis[v])tot++;
        }
    tot/=2;
    if(s[0]>tot)ans1+=tot;
    else if(s[0]=dfn[x])
            {
                memset(vis,0,sizeof(vis));
                s[0]=0;
                do{
                    s[++s[0]]=_stack[--top];
                    vis[_stack[top]]=true;

                }while(_stack[top]!=v);
                s[++s[0]]=x;
                vis[x]=1;
                work();
            }
        }
        else low[x]=min(low[x],dfn[v]);
    }
}
int main()
{
	freopen("way.in","r",stdin);
	freopen("way.out","w",stdout);
    while(scanf("%d%d",&n,&m)!=EOF)
    {
    	int i=-1;
        if(n==0&&m==0) break;
        
        memset(low,0,sizeof(low));
        memset(dfn,0,sizeof(dfn));
        memset(s,0,sizeof(s));
        memset(vis,0,sizeof(vis));
        memset(last,-1,sizeof(last));
        
		ans1=ans2=len=top=cnt=0;
        for(;++i

【HNOI2012_BZOJ2730】矿场搭建

题目描述
煤矿工地可以看成是由隧道连接挖煤点组成的无向图。

为安全起见，希望在工地发生事故时所有挖煤点的工人都能有一条出路逃到救援出口处。于是矿主决定在某些挖煤点设立救援出口，使得无论哪一个挖煤点坍塌之后，其他挖煤点的工人都有一条道路通向救援出口。

请写一个程序，用来计算至少需要设置几个救援出口，以及不同最少救援出口的设置方案总数。

输入格式
输入文件有若干组数据，每组数据的第一行是一个正整数 N（N≤500），表示工地的隧道数，

接下来的 N 行每行是用空格隔开的两个整数 S 和 T，表示挖煤点 S 与挖煤点 T 由隧道直接连接。输入数据以 0 结尾。

输出格式
输入文件中有多少组数据，输出文件 output.txt 中就有多少行。

每行对应一组输入数据的 结果。其中第 i 行以 Case i: 开始（注意大小写，Case 与 i 之间有空格，i 与:之间无空格，: 之后有空格），其后是用空格隔开的两个正整数，第一个正整数表示对于第 i 组输入数据至少需 要设置几个救援出口，第二个正整数表示对于第 i 组输入数据不同最少救援出口的设置方案总 数。

输入数据保证答案小于 2^64。输出格式参照以下输入输出样例。

样例数据
input

9
1 3
4 1
3 5
1 2
2 6
1 5
6 3
1 6
3 2
6
1 2
1 3
2 4
2 5
3 6
3 7
0
output

Case 1: 2 4
Case 2: 4 1
Case 1 的四组解分别是(2,4),(3,4),(4,5),(4,6)；

Case 2 的一组解为(4,5,6,7)。

数据规模与约定
hnoi2012

时间限制：1s
空间限制：256MB

首先我们知道，对于这张图，我们可以枚举坍塌的是哪个点，对于每个坍塌的点，最多可以将图分成若干个不连通的块，这样每个块我们可能需要一个出口才能满足题目的要求，枚举每个坍塌的点显然是没有意义的，我们只需要每个图的若干个割点，这样除去割点的图有若干个块，我们可以求出只与一个割点相连的块，这些块必须要一个出口才能满足题目的要求，每个块内有块内个数种选法，然后将所有满足一个割点相连的块的点数连乘就行了
对于每个与一个割点相连的块必须建出口可以换一种方式理解，我们将每个块看做一个点，那么算上割点之后，这张图就变成了一颗树，只有叶子节点我们需要建立出口，因为对于非叶子节点我们不论断掉哪个点我们都有另一种方式相连，这里的叶子节点就是与一个割点相连的块。
最后还有个特判，就是对于一个双连通图，我们至少需要选取两个点作为出口，因为如果就选一个，可能该点为坍塌点，这时我们就任选两个点就行了，方案数为点数(点数-1)>>1。
先tarjan求一下所有的点双。 然后对于每一个点双，分类讨论： 1、只有一个割点，必须选一个非割点。 2、有>=2个割点，不用选 3、有0个割点，必须选俩。*

代码呢~？
就在下面~

#include
using namespace std;
const int N=1005;
struct ss
{
    int to,next;
}e[N*2];
int n,m,len,cnt,tot,top,ji,root,maxx;
int last[N],dfn[N],low[N];
bool vis[N];
void insert(int x,int y)
{
	e[++len].next=last[x];
	e[len].to=y;
	last[x]=len;
}
void tarjan(int x)
{
    int flag=0,i=last[x];
    for(dfn[x]=low[x]=++len;i;i=e[i].next)
    {
        int v=e[i].to;
        if(dfn[v]==0)
        {
            ++flag;
            tarjan(v);
            if(low[v]>=dfn[x])vis[x]=1,++cnt;
        }
        low[x]=min(low[x],low[v]);
    }
    if(x==root&&flag==1)vis[x]=0,--cnt;
}
void dfs(int x,int t)
{
	int i=last[x];
    dfn[x]=t;
    if(vis[x]==1)
	{
	    ++cnt;
		return;
	}
    for(++tot;i;i=e[i].next)
    {
        int v=e[i].to;
        if(dfn[v]!=t)dfs(v,t);
    }
}
int main()
{
	freopen("input.in","r",stdin);
	freopen("output.out","w",stdout);
	
    while(scanf("%d",&m)!=EOF)
    {
    	int i=0;
        if(!m)break;
        memset(last,0,sizeof(last));
        for(len=0,maxx=-1000,ji++;++i<=m;)
        {
            int x,y;
            scanf("%d%d",&x,&y);
            insert(x,y);
			insert(y,x);
            maxx=max(maxx,max(x,y));
        }
        
        memset(vis,0,sizeof(vis));
        memset(low,0,sizeof(low));
        memset(dfn,0,sizeof(dfn));
        
        for(len=cnt=0,i=0;++i<=maxx;)
        {
            root=i;
            if(dfn[i]==0)tarjan(i);
        }
        if(!cnt)printf("Case %d: 2 %d\n",ji,maxx*(maxx-1)/2);
        else
        {
            len=0;
            memset(dfn,0,sizeof(dfn));
			long long ans=1;
            for(i=0,top=0;++i<=maxx;)
                if(dfn[i]==0&&vis[i]==0)
                {
                    tot=cnt=0;
                    dfs(i,i);
                    if(cnt==0)top+=2,ans*=(long long)((tot-1)*tot/2);
                    if(cnt==1)top+=1,ans*=(long long)(tot); 
                }
            printf("Case %d: %d %lld\n",ji,top,ans);
        }
    }
    return 0;
}

---

那么~就结束了 谢谢观赏~~
附注：这是我第一次用Markdown编辑，如有不足请谅解