(二)Softmax回归
1、分类模型
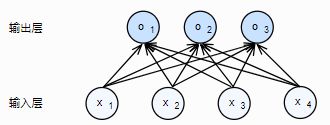
分类模型,例如Softmax回归。和线性回归不同,Softmax回归的输出单元从一个变成了多个。Softmax回归是一个单层神经网络。
2、Softmax运算
设带下标的w和b分别为Softmax回归的权重和偏差参数。给定单个图片的输入特征 x1,x2,x3,x4 x 1 , x 2 , x 3 , x 4 ,有
o1=x1w11+x2w21+x3w31+x4w41+b1,o2=x1w12+x2w22+x3w32+x4w42+b2,o3=x1w13+x2w23+x3w33+x4w43+b3. o 1 = x 1 w 11 + x 2 w 21 + x 3 w 31 + x 4 w 41 + b 1 , o 2 = x 1 w 12 + x 2 w 22 + x 3 w 32 + x 4 w 42 + b 2 , o 3 = x 1 w 13 + x 2 w 23 + x 3 w 33 + x 4 w 43 + b 3 .
在得到输出层的三个输出后,我们需要预测输出分别为lable1、lable12和lable3的概率。不妨设它们分别为 y^1,y^2,y^3 y ^ 1 , y ^ 2 , y ^ 3 。下面,我们通过对 o1,o2,o3 o 1 , o 2 , o 3 做Softmax运算,得到模型最终输出
y^1=exp(o1)∑3i=1exp(oi),y^2=exp(o2)∑3i=1exp(oi),y^3=exp(o3)∑3i=1exp(oi). y ^ 1 = exp ( o 1 ) ∑ i = 1 3 exp ( o i ) , y ^ 2 = exp ( o 2 ) ∑ i = 1 3 exp ( o i ) , y ^ 3 = exp ( o 3 ) ∑ i = 1 3 exp ( o i ) .
Softmax运算中的三式记作
y^1,y^2,y^3=Softmax(o1,o2,o3). y ^ 1 , y ^ 2 , y ^ 3 = Softmax ( o 1 , o 2 , o 3 ) .
3、交叉熵损失函数
Softmax回归使用了交叉熵损失函数(cross-entropy loss)。真实标分别对应离散值y1,y2,y3,它们的预测概率分别为 y1,y2,y3 y 1 , y 2 , y 3 。为了便于描述,设样本i的标签的被预测概率为 plabeli=y^i p label i = y ^ i 。例如,如果样本i的标签为y3,那么 plabeli=y^3 p label i = y ^ 3 。直观上,训练数据集上每个样本的真实标签的被预测概率越大(最大为1),分类越准确。假设训练数据集的样本数为n。由于对数函数是单调递增的,且最大化函数与最小化该函数的相反数等价,我们希望最小化
ℓ(Θ)=−1n∑i=1nlogplabeli ℓ ( Θ ) = − 1 n ∑ i = 1 n log p label i
其中 Θ Θ 为模型参数。该函数即 交叉熵损失函数。在训练Softmax回归时,我们将使用优化算法来迭代模型参数并不断降低损失函数的值。