【算法】Trie数(前缀树/字典树)简介及Leetcode上关于前缀树的题
前几天同学面今日头条被问到了Trie树,刚好我也对于Trie树这种数据结构不是很熟悉,所以研究了一下前缀树,然后把Leetcode上关于前缀树的题都给做了一遍。
Leetcode上关于前缀树的题有如下:
- 208. Implement Trie (Prefix Tree)这道题是实现一个前缀树,作为基础题啦
- Add and Search Word - Data structure design这道题是把前缀树做一个简单的变形
- 472. Concatenated Words
- 212. Word Search II
- 421. Maximum XOR of Two Numbers in an Array
Trie简介
Trie树,又称单词查找树或键树,是一种树形结构,是一种哈希树的变种。
典型应用是
1. 用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。
2. 用于前缀匹配,比如我们在搜索引擎中输入待搜索的字词时,搜索引擎会给予提示有哪些前缀。
它的优点是:最大限度地减少无谓的字符串比较,查询效率比哈希表高。缺点就是空间开销大。
前缀树
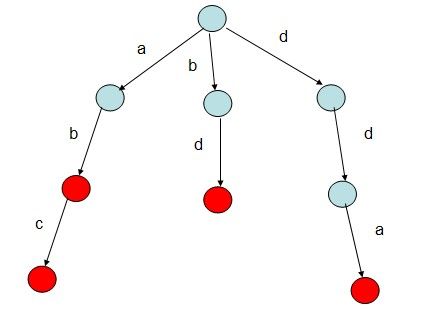
有如下特点:
1. 根节点不包含字符,除根节点外每一个节点都只包含一个字符。
2. 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
3. 每个节点的所有子节点包含的字符都不相同。
4. 如果字符的种数为n,则每个结点的出度为n,这也是空间换时间的体现,浪费了很多的空间。
5. 插入查找的复杂度为O(n),n为字符串长度。
对于Leetcode上208. Implement Trie (Prefix Tree)这道题就是前缀树的一个实现,代码如下:
class TrieNode {
public:
//因为题目中是说字符都是小写字母。所以只用26个子节点就好
TrieNode *child[26];
bool isWord;
TrieNode() : isWord(false){
for (auto &a : child) a = nullptr;
}
}; //这个是前缀树的每个节点的构造,其中isWord表示是否有以这个节点结尾的单词
//下面这个就是前缀树所包含的操作了
class Trie {
private:
TrieNode *root;
public:
/** Initialize your data structure here. */
Trie() {
root = new TrieNode();
}
/** Inserts a word into the trie. */
//插入操作
void insert(string word) {
TrieNode * nptr = root;
for (int i = 0; i//每次判断接下来的这个节点是否存在,如果不存在则创建一个
if (nptr->child[word[i] - 'a'] == NULL)
nptr->child[word[i] - 'a'] = new TrieNode();
nptr = nptr->child[word[i] - 'a'];
}
nptr->isWord = true;
}
/** Returns if the word is in the trie. */
//搜索操作,判断某一个字符串是否存在于这个字典序列中
bool search(string word) {
if (word.size() == 0)
return false;
TrieNode *nptr = root;
for (int i = 0; iif (nptr->child[word[i] - 'a'] == NULL)
return false;
nptr = nptr->child[word[i] - 'a'];
}
//判断是否有以当前节点为结尾的字符串
return nptr->isWord;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
//判断是否存在以prefix为前缀的字符串,其实跟search操作几乎一样啦,只不过最后返回的时候不用判断结尾节点是否为一个叶子结点
bool startsWith(string prefix) {
if (prefix.size() == 0)
return false;
TrieNode *nptr = root;
for (int i = 0; iif (nptr->child[prefix[i] - 'a'] == NULL)
return false;
nptr = nptr->child[prefix[i] - 'a'];
}
return true;
}
}; Leetcode上关于Trie的题
211. Add and Search Word - Data structure design
211. Add and Search Word - Data structure design
这道题题意是创建一个数据结构,能够有插入字符串和查找是否存在字符串的操作,但是查找操作需要支持模糊查找,即要满足如下的条件
addWord(“bad”)
addWord(“dad”)
addWord(“mad”)
search(“pad”) -> false
search(“bad”) -> true
search(“.ad”) -> true
search(“b..”) -> true
这道题的思路就是一个前缀树变形,只不过在查找操作的时候,如果碰见了「.」则将其每个子节点都搜索一遍,相当于一个DFS了
class TrieNode {
public:
TrieNode *child[26];
bool isWord;
TrieNode() : isWord(false){
for (auto &a : child) a = NULL;
}
};
class WordDictionary {
private:
TrieNode *root;
public:
/** Initialize your data structure here. */
WordDictionary() {
root = new TrieNode();
}
/** Adds a word into the data structure. */
void addWord(string word) {
TrieNode* nptr = root;
for(int i=0;i'a';
if(nptr->child[k] == NULL)
nptr->child[k] = new TrieNode();
nptr = nptr->child[k];
}
nptr->isWord = true;
}
bool dfs(string word,TrieNode *root){
if(root == NULL)
return false;
if(word.size() == 0)
return root->isWord;
TrieNode* nptr = root;
if(word[0] != '.'){
int k = word[0]-'a';
if(nptr->child[k] == NULL)
return false;
return dfs(word.substr(1),nptr->child[k]);
}else{
//如果该字符为「.」则搜索其每一个子节点。
bool tmp = false;
for(int j=0;j<26;j++)
if(dfs(word.substr(1),nptr->child[j]) == true)
return true;
return false;
}
}
/** Returns if the word is in the data structure. A word could contain the dot character '.' to represent any one letter. */
bool search(string word) {
return dfs(word,root);
}
}; 472. Concatenated Words
472. Concatenated Words
这道题就是给一组字符串,然后找出其中所有可以用其他字符串拼接成的字符串
Input: [“cat”,”cats”,”catsdogcats”,”dog”,”dogcatsdog”,”hippopotamuses”,”rat”,”ratcatdogcat”]
Output: [“catsdogcats”,”dogcatsdog”,”ratcatdogcat”]
Explanation:
“catsdogcats” can be concatenated by “cats”, “dog” and “cats”;
“dogcatsdog” can be concatenated by “dog”, “cats” and “dog”;
“ratcatdogcat” can be concatenated by “rat”, “cat”, “dog” and “cat”.
这道题其实非常的来气,因为这道题用C++写的话Trie过不了,在最后一组数据中会报Memory超过限制,但是用Java写的话,就不会有问题。【看到有同学说是因为Leetcode中用C++写的话需要释放内存,否则运行多组case会爆memory,但是我实测的结果发现加上手动释放内存依然过不了】
看discuss里面有个深度优化的Trie写法能够解决这个问题:C++ Solutions, Backtrack, DP, or Trie.问题里的第二楼
不过通用的Trie解法如下
class TrieNode {
public:
TrieNode *child[26];
bool isWord;
TrieNode() : isWord(false) {
for (auto &a : child) a = NULL;
}
};
class Trie {
private:
TrieNode *root;
public:
/** Initialize your data structure here. */
Trie() {
root = new TrieNode();
}
/** Inserts a word into the trie. */
void insert(string word) {
TrieNode * nptr = root;
for (int i = 0; iif (nptr->child[word[i] - 'a'] == NULL)
nptr->child[word[i] - 'a'] = new TrieNode();
nptr = nptr->child[word[i] - 'a'];
}
nptr->isWord = true;
}
/** Returns if the word is in the trie. */
//这个函数返回的是所有能够切分一个字符串的位置
vector<int> search(string word) {
vector<int> res;
TrieNode *nptr = root;
for (int i = 0; iif (nptr->isWord)
res.push_back(i);
if (nptr->child[word[i] - 'a'] == NULL)
return res;
nptr = nptr->child[word[i] - 'a'];
}
return res;
}
};
class Solution {
public:
Trie trie;
unordered_map<string, int> mark;
static bool cmp(const string &a,const string &b){
return a.size()//k这个主要用来记录是否是最外层的,如果不是最外层的话,则只需要喊str这个串本身是否含在已包含的字符串中就好。
bool judge(string& str, int k) {
vector<int> res = trie.search(str);
//从末端进行搜索,能够优化一些效率
reverse(res.begin(),res.end());
if (k == 1) {
if (mark.find(str) != mark.end())
return true;
}
for (int i = 0; istring tmp = str.substr(res[i]);
if (judge(tmp, 1)) {
mark[str] = 1;
return true;
}
}
return false;
}
vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {
sort(words.begin(),words.end(),cmp);
vector<string> res;
for (auto && i : words) {
if(i.size() == 0)
continue;
if (judge(i, 0))
res.push_back(i);
trie.insert(i);
mark[i] = 1;
}
return res;
}
}; 这个过不去,我也是非常的无奈,最后只要用了个hashmap暴力做,代码如下:
unordered_set<string> mark;
static bool cmp(const string &a,const string &b){
return a.size()bool judge(string &word,int pos,string str) {
if(pos == word.size()){
if(mark.find(str)!= mark.end())
return true;
return false;
}
str += word[pos];
if(mark.find(str) != mark.end()){
string tmp = "";
if(judge(word,pos+1,""))
return true;
}
return judge(word,pos+1,str);
}
vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {
sort(words.begin(),words.end(),cmp);
vector<string> res;
for (auto && i : words) {
if(i.size() == 0)
continue;
if (judge(i, 0,""))
res.push_back(i);
mark.insert(i);
}
return res;
} 212. Word Search II
212. Word Search II
这道题的减弱版是word search I 是给一个图,然后看如果沿着某一个路径的话,是否存在一个给定的字符串,那就跑一个DFS加回溯就好
如果是一组字符串,则需要做一个查询优化了,就是建一个Trie数,每次从某个节点开始DFS这个图,然后再搜索的时候,也对应着在搜索这颗Trie,如果搜到了以某一个leaf节点,则其就是一个结果,然后再将其置为非叶子结点,避免重复查找。
具体在实现上,有几个细节:
1. 每个叶子结点可以就存着这个字符串是什么
2. 其次这道题只用到了Trie的建树操作即可,剩下的search操作是不需要的,所以只用一个TrieNode数据结构就可以了
vector<string> res;
struct TrieNode{
vectorif(nptr->child[word[i] - 'a'] == nullptr)
nptr->child[word[i] - 'a'] = new TrieNode();
nptr = nptr->child[word[i] - 'a'] ;
}
nptr->word = word;
}
return root;
}
void dfs(TrieNode* root,vector<vector<char>>& board,int i,int j){
//一定要注意这个函数中,几个跳出循环的先后顺序,一定一定要注意
if(root == nullptr ) return;
if(root->word.size() >0){
res.push_back(root->word);
root->word = "";
}
int n = board.size();
int m = board[0].size();
if(i<0 ||j <0||i>=n|| j>=m)
return;
if(board[i][j] == 0) return;
//tmp是用来回溯的
int tmp = board[i][j]-'a';
board[i][j] = 0;
dfs(root->child[tmp],board,i-1,j);
dfs(root->child[tmp],board,i,j-1);
dfs(root->child[tmp],board,i+1,j);
dfs(root->child[tmp],board,i,j+1);
board[i][j] = tmp+'a';
return;
}
vector<string> findWords(vector<vector<char>>& board, vector<string>& words) {
auto root = buildTrie(words);
int n = board.size();
int m = board[0].size();
for(int i =0 ;ifor(int j = 0;jreturn res;
} 421. Maximum XOR of Two Numbers in an Array
421. Maximum XOR of Two Numbers in an Array
这道题是给一个数组,让找出其中两两异或之后和最大的结果。需要用 O(n) 的算法复杂度
这道题之前在【算法】按位Bit By Bit的方法里面有介绍过按位依次搜索的算法,这里用Trie的方法可以再做一遍。
思路就是先将数组中所有数构建一棵Trie,然后再扫一遍数组中的每个数,遇到能够异或得到1的,则这一位是1,否则是0.
struct TrieNode{
vector其他需要特别注意到的地方
以上的几道题都用到了递归/DFS的写法,一定要注意递归终止条件的先后顺序,一定一定要注意,今天碰到了好多的坑点。