【机器学习】信息量，信息熵，交叉熵，KL散度和互信息（信息增益）

首先先强烈推荐一篇外文博客Visual Information Theory这个博客的博主colah是个著名的计算机知识科普达人，之前非常著名的那篇LSTM讲解的文章也是他写的。这篇文章详细讲解了信息论中许多基本概念的来龙去脉，而且非常的直观用了大量的图片，和形象化的解释。

信息量

信息量用一个信息所需要的编码长度来定义,而一个信息的编码长度跟其出现的概率呈负相关,因为一个短编码的代价也是巨大的,因为会放弃所有以其为前缀的编码方式,比如字母”a”用单一个0作为编码的话,那么为了避免歧义,就不能有其他任何0开头的编码词了.所以一个词出现的越频繁,则其编码方式也就越短,同时付出的代价也大.

I=log2(1p(x))=−log2(p(x))

信息熵

而信息熵则代表一个分布的信息量,或者编码的平均长度

H(p)=∑xp(x)log2(1p(x))=−∑xp(x)log2(p(x))

即信息量的均值

交叉熵 cross-entropy

交叉熵本质上可以看成,用一个猜测的分布的编码方式去编码其真实的分布,得到的平均编码长度或者信息量

Hp(q)=∑xq(x)log2(1p(x))

如上面的式子,用猜的的p分布,去编码原本真是为q的分布,得到的信息量

交叉熵 cross-entropy在机器学习领域的作用

交叉熵cross-entropy在机器学习领域中经常作为最后的损失函数
为什么要用cross-entropy呢，他本质上相当于衡量两个编码方式之间的差值，因为只有当猜测的分布约接近于真实分布，则其值越小。
比如根据自己模型得到的A的概率是80%，得到B的概率是20%，真实的分布是应该得到A，则意味着得到A的概率是100%，所以

L=−∑iyilog(p(xi))+(1−yi)log(1−p(xi))

在LR中用cross-entry比平方误差方法好在：

1. 在LR中，如果用平方损失函数，则损失函数是一个非凸的，而用cross-entropy的话就是一个凸函数
2. 用cross-entropy做LR求导的话，得到的导数公式如下
   
   ∂L∂θj=−∑i(yi−p(xi))xij
   
   而用平方损失函数的话，其求导结果为
   
   ∂L∂θj=−∑i(yi−p(xi))p′(xi)
   
   平方损失函数中会出现 p′(xi) 而sigmoid函数的导数会出现梯度消失的问题【一些人称之为饱和现象】

KL散度

KL散度/距离是衡量两个分布的距离,KL距离一般用 D(q||p) 或者 Dq(p) 称之为q对p的相对熵

Dq(p)=Hq(p)−H(p)=∑xq(x)log2(q(x)p(x))

KL散度与cross-entropy的关系

用图像形象化的表示二者之间的关系可以如下图：

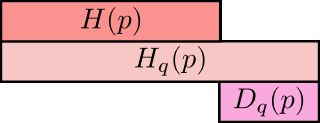
上面是q所含的信息量/平均编码长度 H(p)
第二行是cross-entropy，即用q来编码p所含的信息量/平均编码长度|或者称之为q对p的cross-entropy
第三行是上面两者之间的差值即为q对p的KL距离

非负性证明

根据上图显然其为非负的，但是怎么去证明呢，还是利用琴生不等式

Dq(p)=∑xq(x)log2(q(x)p(x))

=−∑xq(x)log2(p(x)q(x))

=−E(log2(p(x)q(x)))

≥log2E(p(x)q(x))

=log2∑xq(x)(p(x)q(x))

=log2∑xp(x)

因为 ∑xp(x)=1
所以上式

Dq(p)≥0

非负性证明完成

联合信息熵和条件信息熵

下面几条我们要说的是联合分布中（即同一个分布中）的两个变量相互影响的关系，上面说的KL和cross-entropy是两个不同分布之间的距离度量【个人理解是KL距离是对于同一个随机事件的不同分布度量之间的距离，所以是1.同一随机事件*2.不同分布*】。

联合信息熵：

H(X,Y)=∑x,yp(x,y)log2(1p(x,y))

条件信息熵：

H(X|Y)=∑yp(y)∑xp(x|y)log2(1p(x|y))

    =∑x,yp(x,y)log2(1p(x|y))

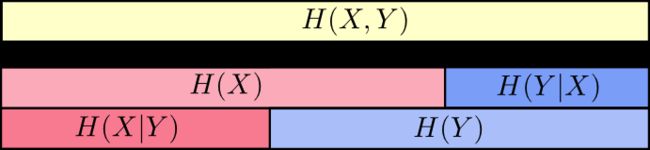
举个例子，更容易理解一些，比如天气是晴天还是阴天，和我穿短袖还是长袖这两个事件其可以组成联合概率分布 H(X,Y) 所以对应着上面的第一条，而对于 H(x) 来说就是下面第二横行，因为两个时间加起来的信息量肯定是大于单一一个事件的信息量的。像 H(x) 对应着今天天气分布的信息量。
而今天天气和我今天穿衣服这两个随机概率事件并不是独立分布的，所以如果已知今天天气的情况下，我的穿衣的信息量/不确定程度是减少了的。
所以当已知 H(x) 这个信息量的时候，联合分布 H(X,Y) 剩余的信息量就是 条件熵：

H(Y|X)=H(X,Y)−H(X)

根据上面那个图，也可以通俗的理解为已知X的情况下，H(X,Y)剩余的信息量

互信息（信息增益）

互信息就是一个联合分布中的两个信息的纠缠程度/或者叫相互影响那部分的信息量

I(X,Y)=H(X)+H(Y)−H(X,Y)

I(X,Y)=H(Y)−H(Y|X)

决策树中的信息增益就是互信息，决策树是采用的上面第二种计算方法，即把分类的不同结果看成不同随机事件Y，然后把当前选择的特征看成X，则信息增益就是当前Y的信息熵减去已知X情况下的信息熵。

通过下图的刻画更为直观一些

以上图可以清楚的看到互信息 I(X,Y) 的不同求法
这里还有另外一个量叫variation of information【不知道中文名叫啥】

V(X,Y)=H(X,Y)−I(X,Y)

Variation of information度量了不同随机变量之间的差别，如果 V(X,Y)=0 说明这两个变量是完全一致的，其约大说明两个变量越独立。
这里再注意一下Variation of information和KL距离的差别：
Variation of information是联合分布中（即 同一个分布中）的两个变量相互影响的关系
KL和cross-entropy是 两个不同分布之间的距离度量

非负性证明

I(X,Y)=H(X)+H(Y)−H(X,Y)

=−∑x,yp(x,y)(log(p(x))+log(p(y))−log(p(x,y)))

=−∑x,yp(x,y)(log(p(x)p(y)p(x,y)))

=D(P(X,Y)||P(X)P(Y))

即互信息可以转化成两个分布 P(X,Y) 和 P(X)P(Y) 之间的KL距离，而KL距离的非负性在上面已经被证明过了，所以

I(X,Y)≥0