集成学习:让算法和算法赛跑
文章目录
- 集成学习的基本概念
- 构建弱分类器:决策树
- 自助采样法
- bootstrapping
- bootstrapping的核心思想
- bootstrapping与permutation的区别
- bagging
- boosting
- 为何bagging会降低variance,boosting降低bias?
- 更多参考阅读:
集成学习的基本概念
集成学习的概念有点像竞争社会,让算法之间竞争,决出最好的结果。如果底层的算法(或者说个体学习器)是同样的只是初始化参数不同,就称为同质集成。如果底层算法的基因都不一样,来自不同的机器学习门派,就称为异质集成。
个体学习器经常设置为多个不同的机器学习算法,这样做保证了个体学习期相互独立性的要求。例如支持向量机(SVM)、线性回归、k近邻、二元决策树等。但是这样做的缺点是每个个体学习期都有不同的参数,需要分别调参,最要命的是,每个模型对输入数据的要求也不一样。这样一来,问题建模的过程反而又复杂了。
因此,在应用集成方法时候,关键是生成大量近似独立模型——这些个体学习器便于调参,输入参数要求一致,易于集成。这里,我们以二元决策树为个体学习器,上层算法以某种方式使得使得个体模型相对独立。具体来说,常见得上层算法有:投票(bagging)、提升(boosting)和随机森林(random forests)。
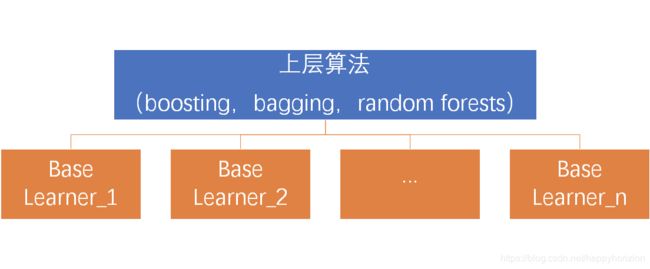
构建弱分类器:决策树
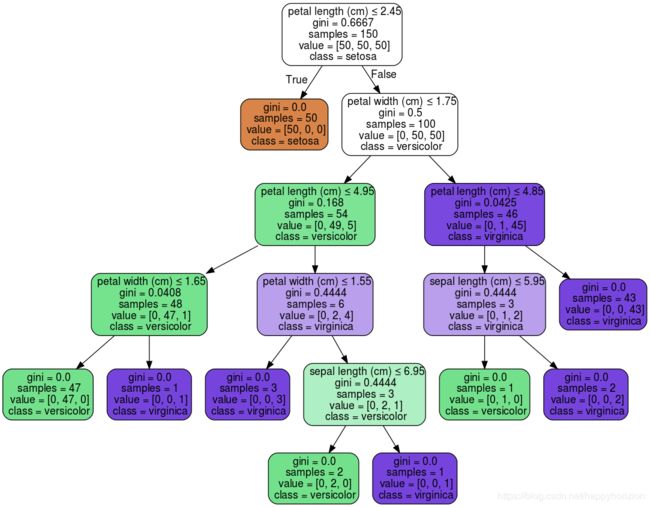
二元决策树可以看作是简单的条件选择,基于某个特性做“是”或者“否”的判断。每次决策后,可能会引出另外一个决策,或者,生成最终的结果。最上面的节点称为根节点(root node)。根节点通常是特别重要的性质(变量),决策树的深度定义为从上到下遍历树的最长路径。例如下面的例子中,这个决策树的深度就是5.
import numpy as np
from sklearn import tree
from sklearn.tree import DecisionTreeRegressor
from sklearn.externals.six import StringIO
# a simple data set with y = x + random
nPoints = 100
xPlot = np.linspace(-0.5, 0.5, 100, endpoint=False)
x = [[xi] for xi in xPlot]
# add random noise
np.random.seed(1)
y = [xi + np.random.normal(scale=0.1) for xi in xPlot]
plot.plot(xPlot,y)
plot.axis('tight')
plot.xlabel('x')
plot.ylabel('y')
plot.show()
# decision tree with 1 layer
simpleTree1 = DecisionTreeRegressor(max_depth=1)
simpleTree1.fit(x,y)
with open("simpleTree1.dot",'w') as f:
f = tree.export_graphviz(simpleTree1, out_file=f)
# decision tree with 2 layers
simpleTree2 = DecisionTreeRegressor(max_depth=2)
simpleTree2.fit(x, y)
# draw the tree
with open("simpleTree2.dot",'w') as f:
f = tree.export_graphviz(simpleTree2, out_file=f)
# compare prediction with true
yHat1 = simpleTree1.predict(x)
yHat2 = simpleTree2.predict(x)
plot.figure()
plot.plot(xPlot, y, label='True_y')
plot.plot(xPlot, yHat1, label='Predict_y1', linestyle="--")
plot.plot(xPlot, yHat2, label='Predict_y2', linestyle=":")
plot.legend(bbox_to_anchor=(1, 0.3))
plot.axis('tight')
plot.xlabel('x')
plot.ylabel('y')
plot.show()
自助采样法
bootstrapping
在介绍Bagging和Boosting之前,首先介绍一下Bootstraping,即自助法:它是一种有放回的抽样方法(可能抽到重复的样本)。它是非参数统计中一种重要的通过估计统计量方差进而进行区间估计的统计方法。
bootstrapping的核心思想
Bootstrap的思想,是生成一系列bootstrap伪样本,每个样本是初始数据有放回抽样。通过对伪样本的计算,获得统计量的分布。例如,要进行1000次bootstrap,求平均值的置信区间,可以对每个伪样本计算平均值。这样就获得了1000个平均值。对着1000个平均值的分位数进行计算, 即可获得置信区间。已经证明,在初始样本足够大的情况下,bootstrap抽样能够无偏得接近总体的分布。
主要步骤:
1)根据抽出的样本计算统计量T。
2)重复上述N次(一般大于1000),得到统计量T。
3)计算上述N个统计量T的样本方差,得到统计量的方差。
Bootstrap实质上是一种再抽样过程,相对于其他方法,在小样本时也具有较好效果。
参见wiki百科关于bootstrapping方法的介绍:https://en.wikipedia.org/wiki/Bootstrapping_(statistics)
bootstrapping与permutation的区别
Permutation test 置换检验是Fisher于20世纪30年代提出的一种基于大量计算(computationally intensive),利用样本数据的全(或随机)排列,进行统计推断的方法,因其对总体分布自由,应用较为广泛,特别适用于总体分布未知的小样本资料,以及某些难以用常规方法分析资料的假设检验问题。在具体使用上它和Bootstrap Methods类似,通过对样本进行顺序上的置换,重新计算统计检验量,构造经验分布,然后在此基础上求出P-value进行推断。
具体看看这篇博客的例子就明白了:
置换检验:https://www.cnblogs.com/bnuvincent/p/6813785.html
bagging
bagging是并行式集成学习方法最著名的代表,从名字就可以看出,它基于自助采样法。给定包含m个样本的数据集,我们先随即取出一个样本放入采样集中,再把这个样本放回到初始数据集,使得下次采样时该样本仍可能被选,这样,经过m次随机采样操作,我们得到含有m个样本的采样集,初始训练集中有的样本在采样集中多次出现,有的没有出现,我们之前计算过这个比例,大概有63.2%的样本会出现在采样集中。
就这样,我们可以采样出T个样本集,每个样本集合中含m个训练样本,然后基于每个采样集训练出一个基学习器,再将这些学习器进行结合,Bagging通常对分类任务使用简单投票法,对回归任务使用简单平均法/若分类预测时出现两个类收到的票数相同,那么最简单的做法是随机选出一个,也可以进一步考察学习器投票的置信度来确定最终胜者。
bagging方法的主要过程
i) 训练分类器:从整体样本集合中,抽样n* < N个样本 针对抽样的集合训练分类器Ci
ii) 分类器进行投票:最终的结果是分类器投票的优胜结果
boosting
boosting一种典型的基于Bootstrapping思想的应用,其特点是:每一次迭代时训练集的选择与前面各轮的学习结果有关,而且每次是通过更新各个样本权重的方式来改变数据分布。其中主要的是Adaboost (Adaptive boosting),即自适应助推法。
Boosting的算法过程如下:
对于训练集中的每个样本建立权值wi,表示对每个样本的权重, 其关键在与对于被错误分类的样本权重会在下一轮的分类中获得更大的权重(错误分类的样本的权重增加)。
加大分类误差概率小的弱分类器的权值,使其在表决中起到更大的作用,减小分类误差率较大弱分类器的权值,使其在表决中起到较小的作用。每一次迭代都得到一个弱分类器,需要使用某种策略将其组合,成为最终模型,(adaboost给每个迭代之后的弱分类器一个权值,将其线性组合作为最终的分类器,误差小的分类器权值越大。)
关于Boosting的两个核心问题:
1)在每一轮如何改变训练数据的权值或概率分布?
通过提高那些在前一轮被弱分类器分错样例的权值,减小前一轮分对样例的权值,来使得分类器对误分的数据有较好的效果。
2)通过什么方式来组合弱分类器?
通过加法模型将弱分类器进行线性组合,比如AdaBoost通过加权多数表决的方式,即增大错误率小的分类器的权值,同时减小错误率较大的分类器的权值。而提升树通过拟合残差的方式逐步减小残差,将每一步生成的模型叠加得到最终模型。
为何bagging会降低variance,boosting降低bias?
什么是bias/variance tradeoff?引用下图来自coursera:

High variance 是model过于复杂overfit,记住太多细节noise,受outlier影响很大;high bias是underfit,model过于简单,cost function不够好。
2 A- bagging随机选取data的subset,outlier因为比例比较低,参与model training的几率也比较低,所以bagging降低了outliers和noise对model的影响,所以降低了variance。
2 B-boosting minimize loss function by definition minimize bias. 因此降低的是bias。
更多参考阅读:
Boosting的代表是AdaBoost,关于AdaBoost,参照以下帖子:
基本原理:http://www.jianshu.com/p/f2017cc696e6
误差分析:http://www.jianshu.com/p/bfba5a91ba15
AdaBoost与前向分步算法:http://www.jianshu.com/p/a712dff0f388
集成学习-Boosting和Bagging异同:https://blog.csdn.net/Mr_Robert/article/details/84448417
https://www.zhihu.com/question/26760839/answer/68915634