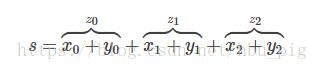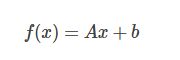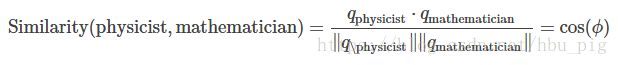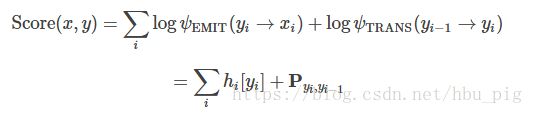使用Pytorch实现NLP深度学习
原文链接:https://pytorch.org/tutorials/beginner/deep_learning_nlp_tutorial.html
本文将会帮助你了解使用Pytorch进行深度学习编程的关键思想。一些章节内容(计算图和梯度)不是Pytorch所特有的,而是所有深度学习工具包都包含的内容。
本文旨在为那些从未接触过其它深度学习框架(如TensorFlow,Theano,Keras,Dynet)从事NLP行业的人。假设你已经拥有了NLP问题的核心知识:词性标注,语言模型等。同样假设你大致了解人工神经网络的原理。即假设你了解前馈神经网络的基本前向传播反向传播算法,并明白这些算法中线性及非线性算法是如何组合的。本文旨在帮你开始写深度学习的代码,基于你有这些知识的前提下。
注意这是关于模型的,而不是数据。对所有的模型来说,我只是创建了包含很少维度的测试示例,这样你可以看到这些权重是如何随着它的训练而变化。如果你想要使用真实数据,你只要拿走模型直接使用就可以。
目录
PyTorch简介
Torch的张量(tensor)库简介
创建张量
张量的运算
改变张量的形状
计算图和自动微分
使用PyTorch进行深度学习
深度学习构建模块:仿射变换,非线性和目标函数
仿射变换
非线性
Softmax与概率
目标函数
优化和训练
在PyTorch中创建网络组件
举例:逻辑回归词袋分类器
词嵌入(Word Embeddings):对词汇的语义进行编码
获取密集词嵌入(dense word embedding)
PyTorch中使用词嵌入
例子:N-Gram语言模型
练习:计算词嵌入:Continuous Bag-of-Words
序列模型和LSTM(Long-Short Term Memory)网络
在PyTorch中使用LSTM
例子:使用LSTM实现词性标注
练习:使用字符级特征增强LSTM词性标注器
高级:动态决策和Bi-LSTM CRF
动态与静态深度学习工具包
Bi-LSTM条件随机场讨论
实现注意事项
练习:判别标注的一种新的损失函数
PyTorch简介
Torch的张量(tensor)库简介
所有的深度学习计算都用到张量,你可以理解为是一个n维的“矩阵”,稍后我们将会确切的看到这意味着什么。首先,我们来看下张量可以用做什么。
import torch
import torch.autograd as autograd
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)#设置随机种子,可以保证多次运行代码的运行结果一致创建张量
张量可以通过torch.Tensor()方法传入一个python的list来创建。
import torch
V_data=[1.,2,3]
V=torch.Tensor(V_data)
print(V)
M_data=[[1.,2,3],[4,5,6]]
M=torch.Tensor(M_data)
print(M)
T_data=[[[1.,2],[3,4]],[[5,6],[7,8]]]
T=torch.Tensor(T_data)
print(T)输出:
tensor([ 1., 2., 3.])
tensor([[ 1., 2., 3.],
[ 4., 5., 6.]])
tensor([[[ 1., 2.],
[ 3., 4.]],
[[ 5., 6.],
[ 7., 8.]]])3维的张量是什么?这样想。如果你有一个向量,它的索引返回一个标量。如果你有一个矩阵,它的索引返回一个向量。而对于一个3维的张量,它的索引返回一个矩阵!
关于术语的解释:当我说张量时,它包括了所有的张量,其中一维的向量,二维的矩阵都是特殊的张量。只有我说3D张量时才是指3维的张量。
print(V[0])
print(M[0])
print(T[0])输出:
tensor(1.)
tensor([ 1., 2., 3.])
tensor([[ 1., 2.],
[ 3., 4.]])
你可以创建任何其他数据类型的张量。默认,是Float。如果创建整数类型的张量,使用torch.LongTensor()。查看文档以获得更多的数据类型,但通常Float和Long是使用最多的。
你可以通过给torch.randn()提供维度信息来创建一个随机数的张量。
x=torch.randn((3,4,5))
print(x)输出:
tensor([[[-1.5256, -0.7502, -0.6540, -1.6095, -0.1002],
[-0.6092, -0.9798, -1.6091, -0.7121, 0.3037],
[-0.7773, -0.2515, -0.2223, 1.6871, 0.2284],
[ 0.4676, -0.6970, -1.1608, 0.6995, 0.1991]],
[[ 0.8657, 0.2444, -0.6629, 0.8073, 1.1017],
[-0.1759, -2.2456, -1.4465, 0.0612, -0.6177],
[-0.7981, -0.1316, 1.8793, -0.0721, 0.1578],
[-0.7735, 0.1991, 0.0457, 0.1530, -0.4757]],
[[-0.1110, 0.2927, -0.1578, -0.0288, 0.4533],
[ 1.1422, 0.2486, -1.7754, -0.0255, -1.0233],
[-0.5962, -1.0055, 0.4285, 1.4761, -1.7869],
[ 1.6103, -0.7040, -0.1853, -0.9962, -0.8313]]])张量的运算
你可以进行任何你想进行的运算
x=torch.tensor([1,2,3])
y=torch.tensor([4,5,6])
z=x+y
print(z)输出
tensor([ 5, 7, 9])点击以下链接来查看可用操作的完整列表。它们不仅仅包含基础的数学运算。
https://pytorch.org/docs/stable/torch.html
我们稍后会使用的一个操作是级联。
#By default, concatenates rows
x_1=torch.randn(2,5)
y_1=torch.randn(3,5)
z_1=torch.cat([x_1,y_1])
print(z_1)
#concatenate columns
x_2=torch.randn(2,3)
y_2=torch.randn(2,2)
z_2=torch.cat([x_2,y_2],1)
print(z_2)输出
tensor([[ 0.6261, -1.1846, -0.5436, 0.6546, -0.5604],
[ 1.8735, -1.3139, 0.1034, -0.0350, -0.5010],
[-0.6748, 0.5247, 0.6635, -0.5871, -0.0938],
[ 0.2649, -0.7554, 2.2387, -0.0361, 0.6611],
[-1.7702, 1.5020, 0.7583, -0.2352, 1.3911]])
tensor([[-0.2167, 1.3546, -0.7955, 0.2682, -0.6354],
[-1.1214, -0.0510, 0.6120, 0.3620, -0.0748]])改变张量的形状
使用.view()方法来改变张量的形状。这个方法被大量使用,因为很多神经网络期望它们的输入具有某种形状。通常,你会在给模型传递数据时使用它。
x=torch.randn(2,3,4)
print(x)
print(x.view(2,12))
print(x.view(2,-1))输出
tensor([[[ 2.0470, -1.1800, 0.6039, 1.3999],
[ 0.8518, 0.3985, 0.1703, -0.4964],
[-0.0290, 0.5847, 0.1747, 0.2283]],
[[ 0.9133, -0.2119, 0.4301, -0.3655],
[ 0.2293, -2.0084, 1.2117, -0.5215],
[ 0.6462, -0.6679, -1.0030, 0.2034]]])
tensor([[ 2.0470, -1.1800, 0.6039, 1.3999, 0.8518, 0.3985, 0.1703,
-0.4964, -0.0290, 0.5847, 0.1747, 0.2283],
[ 0.9133, -0.2119, 0.4301, -0.3655, 0.2293, -2.0084, 1.2117,
-0.5215, 0.6462, -0.6679, -1.0030, 0.2034]])
tensor([[ 2.0470, -1.1800, 0.6039, 1.3999, 0.8518, 0.3985, 0.1703,
-0.4964, -0.0290, 0.5847, 0.1747, 0.2283],
[ 0.9133, -0.2119, 0.4301, -0.3655, 0.2293, -2.0084, 1.2117,
-0.5215, 0.6462, -0.6679, -1.0030, 0.2034]])计算图和自动微分
计算图的概念对于高效的深度学习来说是必不可少的,因为它允许你不必须去编写反向传播的代码。计算图是对你的数据是如何组织变成输出的一个简单说明。因为计算图明确每个参数参与了哪个运算,所以它包含了足够的信息去计算导数。这听起来可能很模糊,让我们使用requires_grad标志来看看它到底是什么吧。
首先,从程序员的角度思考。我们创建的torch.Tensor里面存储了什么东西?明显有数据和形状,也许还有一些别的东西。但是当我们将两个tensor相加,我们得到了一个输出的tensor。这个输出的tensor只知道它自己的数据和形状。并不知道是两个tensor的和。(它有可能是通过读文件得到的,有可能是其他运算的结果)。
如果设置requires_grad=True,张量就会记录它是如何被创建的。
x=torch.tensor([1.,2,3],requires_grad=True)
y=torch.tensor([4.,5,6],requires_grad=True)
z=x+y
print(z)
print(z.grad_fn)输出
tensor([5., 7., 9.], grad_fn=)
所以张量知道自己是怎么产生的。z知道它自己不是从文件读取的数据,也不是乘法或指数运算或balabala的结果。如果你继续跟踪z.grad_fn,你会找到x和y
但是这对计算梯度有什么帮助呢?
s=z.sum()
print(s)
print(s.grad_fn)输出
tensor(21., grad_fn=)
现在,怎么求s对x的第一个分量x0的偏导数?在数学上,我们想要求
![]()
s知道它是由z的求和操作产生的,z知道它是x+y的和。所以
所以s包含了足够信息去计算我们要想要的偏导数为1!
当然这隐藏了它是如何计算导数的细节。这里的要点是s包含足够信息去计算。实际上,PyTorch的开发者编写+和sum()运算是怎么计算梯度并进行反向传播的,这个算法的深入讨论超出了本文范围。
我们使用PyTorch来计算梯度,看下是否正确(注意,如果你调用代码多次,梯度会增加。这是因为PyTorch累计梯度放到.grad属性中,以此为很多模型提供方便。)
s.backward()
print(x.grad)输出
tensor([ 1, 1, 1])理解以下的代码是如何工作的对于你成为一个成功的深度学习编程者来说是至关重要的。
x=torch.randn(2,2)
y=torch.randn(2,2)
print(x.requires_grad,y.requires_grad)
z=x+y
print(z.grad_fn)
x=x.requires_grad_()
y=y.requires_grad_()
z=x+y
print(z.grad_fn)
print(z.requires_grad)
new_z=z.detach()
print(new_z.grad_fn)输出
False False
None
True
None 你也可以通过with torch.no_grad():来取消自动微分
print(x.requires_grad)
print((x**2).requires_grad)
with torch.no_grad():
print((x**2).requires_grad)输出
True
True
False使用PyTorch进行深度学习
深度学习构建模块:仿射变换,非线性和目标函数
深度学习是线性和非线性明智组合。非线性提供了更强大的模型。这节,我们会使用这些组件,生成目标函数,看看模型是如何训练的。
仿射变换
深度学习的核心工作之一是仿射映射,即对于以下的f(x)
对于一个矩阵A和向量x,b。这里要学习的参数是A和b。通常,b被称为偏置项。
PyTorch和其他深度学习框架做的事情和传统的代数学有所不同。它变换输入的一行而不是列。就是说,输出的第i行是输入的第i行经过A的变换(或映射),再加上偏置项。看下面的例子。
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)lin=nn.Linear(5,3)#maps from R^5 to R^3
data=torch.randn(2,5)
print(lin(data))输出
tensor([[ 0.1755, -0.3268, -0.5069],
[-0.6602, 0.2260, 0.1089]])非线性
首先,注意下面的事实,这将解释为什么我们需要非线性。设想我们有两个仿射变换f(x)=Ax+b,g(x)=Cx+d.那么f(g(x))是什么?
f(g(x))=A(Cx+d)+b=ACx+(Ad+b)
AC是一个矩阵,Ad+b是一个向量,所以我们知道两个仿射变换的复合还是一个仿射变换。
因此如果你想要你的神经网络是一个长的仿射变换链条,你需要往模型中增加一些新的东西而不只是单一的仿射变换。
如果我们在两个仿射变换之间增加非线性关系,就不会出现以上的情况,我们就可以建立更多更厉害的模型了。
这里有一些非线性的核函数。tanh(x),sigmod(x),ReLU(x)最常用。你有可能会想:“为什么是这个函数?我能找到特别多的非线性函数。”原因是这些函数可导且容易计算,例如
注意:尽管你可能在别的AI课程学习过一些神经网络使用了默认的sigmod(x),实践中人们经常回避它,这是因为随着网络深度的增长梯度会快速消失。太小的梯度意味着它很难学到什么。大部分人选择使用tanh和ReLU
data=torch.randn(2,2)
print(data)
print(F.relu(data))输出
tensor([[-0.5404, -2.2102],
[ 2.1130, -0.0040]])
tensor([[ 0.0000, 0.0000],
[ 2.1130, 0.0000]])Softmax与概率
函数Softmax(x)也是非线性的,但是它有点特殊,因为它通常会是网络的最后一个运算。这是因为它接收一个实数向量并返回它的概率分布。它的定义如下,x是一个实数的向量,Softmax(x)运算以后x的第i个分量为
这清晰的表明输出是一个概率分布:每个元素非负并且加起来等于1.
你也可以把它想成是把x作为因子做了一次指数运算后再除以常量进行归一化。
data=torch.randn(5)
print(data)
print(F.softmax(data,dim=0))
print(F.softmax(data,dim=0).sum())#sums to 1
print(F.log_softmax(data,dim=0))#log e softmax输出
tensor([ 1.3800, -1.3505, 0.3455, 0.5046, 1.8213])
tensor([ 0.2948, 0.0192, 0.1048, 0.1228, 0.4584])
tensor(1.)
tensor([-1.2214, -3.9519, -2.2560, -2.0969, -0.7801])目标函数
目标函数是你在网络训练过程中需要被最小化的函数,有时也叫作损失函数。这首先通过选择一个训练实例,通过神经网络的运算,然后计算输出的损失。然后通过损失函数的导数来更新模型的参数。直观的说,如果你的模型对它的答案完全自信,但它是错的,你的损失函数会很大。如果模型对它的答案完全自信,结果是正确的,损失函数会很小。
在训练集上最小化损失函数是为了模型能够很好的泛化到开发集、测试集或产品上。举例,负对数似然损失函数,经常在多分类问题上使用。对于有监督的多分类问题,这意味着训练网络要最小化-log(正确输出可能性)函数,也就是最大化log(正确输出可能性)
优化和训练
所以我们可以为实例计算损失函数?我们可以用它做什么?之前我们已经提到了张量是可以代替我们计算微分的。所以,只要loss是一个张量,我们就可以计算所有参数的微分!然后我们可以进行标准的梯度更新。![]() 设是我们要学习的参数,L(
设是我们要学习的参数,L(![]() )是损失函数,
)是损失函数,![]() 是一个正的学习率。那么:
是一个正的学习率。那么:
已经有很多的算法机构在研究,它们不仅仅可以做简单的梯度更新。很多是在训练的时候变化学习率。你不需要关心它们到底做了什么除非你对它特别感兴趣。Torch提供了很多方法在torch.optim库中,它们是完全透明的。使用最简单的梯度更新算法与使用最复杂的一样简单。尝试使用不同的更新算法和参数(如学习率)在优化网络性能方面是很重要的。通常,只要替换SGD为Adam或RMSProp就可以显著地提升性能。
在PyTorch中创建网络组件
在我们把注意力放到NLP之前,让我们创建一个只使用仿射变换和非线性运算PyTorch网络示例。我们将会看到如何进行损失计算,如何使用负对数似然函数,以及如何通过反向传播更新参数。
所有的网络组建应该继承自nn.Module,并且重写父类的forward()方法。就这点来说,是有点公式化的。继承nn.Module使你的组建拥有更多的功能。例如,它可以跟踪所有的可训练的参数,你可以通过.to(device)方法实现在CPU和GPU的切换,这里的device可以是CP设备torch.device("cpu")或者CUDA设备torch.device("cuda:0")
我们写一个接收稀疏词袋表述输出两个类别(”English“,”Spanish“)的概率分布的网络例子,这个模型是逻辑回归。
举例:逻辑回归词袋分类器
我们的模型的输入是用词袋(Bag-of-Words)方式表述的文本,输出是落在两个类别的对数概率。我们为每个单词在词汇表中分配一个索引。例如,这里我们的词汇表就俩单词:“hello”和“world”,它们的索引分别为0和1.句子“hello hello hello hello”的词袋(BoW)方式表示为【4,0】;句子“hello world world hello”表示为【2,2】等。
通用形式可以写为,【Count(hello),Count(world)】
把这个词袋向量表示为x,我们网络的输出为:
也就是说,我们把输入经过一个仿射变换,然后进行了log Softmax运算。
data = [("me gusta comer en la cafeteria".split(), "SPANISH"),
("Give it to me".split(), "ENGLISH"),
("No creo que sea una buena idea".split(), "SPANISH"),
("No it is not a good idea to get lost at sea".split(), "ENGLISH")]
test_data = [("Yo creo que si".split(), "SPANISH"),
("it is lost on me".split(), "ENGLISH")]
word_to_ix = {}
for sent, _ in data + test_data:
for word in sent:
if word not in word_to_ix:
word_to_ix[word] = len(word_to_ix)
print(word_to_ix)
VOCAB_SIZE = len(word_to_ix)
NUM_LABELS = 2
class BoWClassifier(nn.Module):
def __init__(self, num_labels, vocab_size):
super(BoWClassifier, self).__init__()
self.linear = nn.Linear(vocab_size, num_labels)
def forward(self, bow_vec):
return F.log_softmax(self.linear(bow_vec), dim=1)
def make_bow_vector(sentence, word_to_ix):
vec = torch.zeros(len(word_to_ix))
for word in sentence:
ix = word_to_ix[word]
vec[ix] += 1
return vec.view(1, -1)
def make_target(label, label_to_ix):
return torch.LongTensor([label_to_ix[label]])
model = BoWClassifier(NUM_LABELS, VOCAB_SIZE)
for param in model.parameters():
print(param)
with torch.no_grad():
sample = data[0]
bow_vector = make_bow_vector(sample[0], word_to_ix)
log_probs = model(bow_vector)
print(log_probs)
输出
{'en': 3, 'No': 9, 'buena': 14, 'it': 7, 'at': 22, 'sea': 12, 'cafeteria': 5, 'Yo': 23, 'la': 4, 'to': 8, 'creo': 10, 'is': 16, 'a': 18, 'good': 19, 'get': 20, 'idea': 15, 'que': 11, 'not': 17, 'me': 0, 'on': 25, 'gusta': 1, 'lost': 21, 'Give': 6, 'una': 13, 'si': 24, 'comer': 2}
Parameter containing:
tensor([[ 0.1194, 0.0609, -0.1268, 0.1274, 0.1191, 0.1739, -0.1099,
-0.0323, -0.0038, 0.0286, -0.1488, -0.1392, 0.1067, -0.0460,
0.0958, 0.0112, 0.0644, 0.0431, 0.0713, 0.0972, -0.1816,
0.0987, -0.1379, -0.1480, 0.0119, -0.0334],
[ 0.1152, -0.1136, -0.1743, 0.1427, -0.0291, 0.1103, 0.0630,
-0.1471, 0.0394, 0.0471, -0.1313, -0.0931, 0.0669, 0.0351,
-0.0834, -0.0594, 0.1796, -0.0363, 0.1106, 0.0849, -0.1268,
-0.1668, 0.1882, 0.0102, 0.1344, 0.0406]])
Parameter containing:
tensor([ 0.0631, 0.1465])
tensor([[-0.5378, -0.8771]])上面哪个变量的值表示ENGLISH的对数概率?哪个表示SPANISH?我们还没定义它,如果你想要训练它就必须定义它。
label_to_ix={"SPANISH":0,"ENGLISH":1}那就开始训练吧!我们首先通过数据获得它的对数概率,计算损失函数,计算损失函数的梯度,然后更新所有的参数一小步。损失函数由PyTorch的nn库提供。nn.NLLLoss()是我们想要的负log似然损失函数。在torch.optim中也定义了很多优化方法。这里,我们用SGD。
注意NLLLoss的输入是一个对数概率的向量,和一个目标label。它不帮我们计算log概率。这就是为什么我们在网络的最后一层为log_softmax函数。损失函数nn.CrossEntropyLoss()和NLLLoss()类似,不同的是它帮我们做了log_softmax的工作。
# before train, just to see a before-and-after
with torch.no_grad():
for instance, label in test_data:
bow_vector = make_bow_vector(instance, word_to_ix)
log_probs = model(bow_vector)
print(log_probs)
# before train, parameter value
print(next(model.parameters())[:, word_to_ix['creo']])
loss_function = nn.NLLLoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)
# Usually, between 5 and 30 epochs is reasonable.
for epoch in range(100):
for instance, label in data:
# PyTorch accumulates gradients
model.zero_grad()
bow_vec = make_bow_vector(instance, word_to_ix)
target = make_target(label, label_to_ix)
log_probs = model(bow_vec)
loss = loss_function(log_probs, target)
loss.backward()
optimizer.step()
with torch.no_grad():
for instance, label in test_data:
bow_vec = make_bow_vector(instance, word_to_ix)
log_probs = model(bow_vec)
print(log_probs)
print(next(model.parameters())[:, word_to_ix['creo']])输出
tensor([[-0.9297, -0.5020]])
tensor([[-0.6388, -0.7506]])
tensor([-0.1488, -0.1313])
tensor([[-0.2093, -1.6669]])
tensor([[-2.5330, -0.0828]])
tensor([ 0.2803, -0.5605])我们得到了正确的answer!你可以看到测试数据的第一个中Spanish的对数概率比较大,第二个English的对数概率比较大。
现在你已经知道怎么去创建一个PYTorch组件,传递数据给它,做梯度更新。我们已经准备好深入学习NLP了。
词嵌入(Word Embeddings):对词汇的语义进行编码
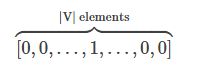
词嵌入实际上是为你的词汇表中的每个单词生成一个实数向量。在NLP中,几乎所有情况下都把单词当做特征!但是首先在计算中应该如何表示一个单词呢?你可以存储它的ascii码,然而它只能告诉你这个单词是什么,并不能告诉你这个单词是什么意思(或许你可以通过它的词缀获取它的词性,或者通过它的大写获取它的特性,但不会很多)。再者,当这些单词组合在一起的时候你怎么表达它们的意思?最后,我们通常想要神经网络输出有意义的结果,它接收的输入是|V|维的,其中V是我们的词汇表,但是通常我们的输出只用很少的维度(比如我们只是想要预测它的标签)。我们应该怎么从一个巨大维度的空间得到一个更小维的空间呢?
如果我们使用one-hot编码替代ascii编码怎么样?即,单词w可以表示以下的形式
其中1是单词w在词汇表的位置。另一个单词的表示将会是在别的地方是1,其它位置全部为0.
one-hot编码方法很简单,但是它有两个巨大的缺点:
- 它假设每个单词是独立的,互不相关。
- 词向量长度巨大。
而我们真正想要的是单词之间的相似性。为什么?让我们看下面的例子。
设想我们建立了一个语言模型。设想在训练数据中我们有以下的句子
- The mathematician ran to the store.
- The physicist ran to the store.
- The mathematician solved the open problem.
现在我们有一个在我们训练数据中没有出现过的新句子:
- The physicist solved the open problem.
我们的语言模型可能表现很不错。但不会比基于以下两点的模型表现的更好:
- 我们已经看到mathematician和physicist在句子中扮演了相同的角色。所以,它们应该有某种关系。
- 新句子中physicist的角色替换为mathematician,我们之前就看到过。
然后推断出physicist很大可能出现新句子中?这就是我们之前提到的相似性概念:我们称语义相似度,不止是简单的拼写相似。这是一种通过连接我们看到过的和没有看到过的,来克服语言稀疏性的技术。这个例子显然依赖于一个基础的语言学假设:出现在相似上下文的词之间语义相关。这个叫做分布假说。
获取密集词嵌入(dense word embedding)
这个问题应该怎么解决?也就是说,我们应该如何为这些单词的语义进行编码?也许你会想到一些语义属性。例如,我们看到mathematicians和physicist都可以跑,所有我们也许可以给这些词在语义属性“is able to run”上打更高的分。想像其他的属性,然后给这些属性打分。
如果一个属性是一个维度,那么我们也许要为一个单词创建一个向量,就像这样:
然后我们可以得到单词之间的 相似性度量:
通常会通过除以它们的长度来正规化:
其中![]() 是两个向量的角度。这样的话,两个极度相似的单词similarity为1,极度不相似的单词similarity为-1.
是两个向量的角度。这样的话,两个极度相似的单词similarity为1,极度不相似的单词similarity为-1.
想下我们之前提到的one-hot编码的稀疏向量,它是一种特殊的词嵌入方式,其中任何两个单词的相似度都为0,并且每个单词拥有一个唯一的语义属性。然而这个的向量是密集的,就是说通常情况下它们的条目不为0。
但是这些新向量有个巨大的痛苦:你可以想象这些决定相似度的数以千计的不同的语义属性,我们要怎么去设置这些属性的值呢?深度学习的核心思想是学习特征,而不是要求程序员去设计它们。所以为什么不让词嵌入作为模型的参数,然后在训练中更新呢?这就是我们将要去做的。原则上,我们将会让网络去学习潜在的语义属性。注意词嵌入可能是无法解释其意义的。这是因为,尽管我们手绘了关于mathematicians和physicist的相似性,例如他们都爱喝咖啡,如果我们要网络去学习的话就会产生一个巨大的词嵌入向量,我们并不知道它的每个属性代表什么。他们的意义和隐含的语义属性类似,但绝大部分我们都无法去解释它到底代表的是什么。
总之,词嵌入是一个单词的语义的表示,有效的编码了可能与当前任务相关的语义信息。你也可以嵌入别的东西:词性标签,解析树,任何东西!特征嵌入的思想是该领域的核心。
PyTorch中使用词嵌入
在我们进行一个例子和练习之前,通常如何在PyTorch中使用词嵌入去做深度学习有一些注意的地方。和我们为每一个单词定义one-hot向量需要为每个单词定义一个索引类似,在使用词嵌入时我们也需要为每个单词定义一个索引。这些将成为我们查找字典的 key。也就是说,嵌入被存储在|V|*D的矩阵中,其中D是嵌入的维度,单词的嵌入存储在通过索引i检索到此矩阵的第i行。在我的所有代码中,单词到所以的映射存储在名为word_to_ix的字典中。
模型允许你通过torch.nn.Embedding使用嵌入,它需要两个参数:词汇表的大小,嵌入的维度。
如果想要获取张量的索引值,你必须使用torch.LongTensor(因为切片是整型的,不是浮点型)
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)word_to_ix = {"hello": 0, "world": 1}
embeds = nn.Embedding(2, 5) # 2words in vocab,5 dimensional embeddings
lookup_tensor = torch.tensor([word_to_ix['hello']], dtype=torch.long)
hello_embeds = embeds(lookup_tensor)
print(hello_embeds)输出
tensor([[ 0.6614, 0.2669, 0.0617, 0.6213, -0.4519]])例子:N-Gram语言模型
回想在n-gram语言模型中,给你一个序列的单词w,我们想要计算
其中![]() 是指这个单词序列的第i个。
是指这个单词序列的第i个。
在这个例子中,我们将会计算训练数据上的损失函数并更新参数进行反向传播
CONTEXT_SIZE = 2
EMBEDDING_DIM = 10
test_sentence = """When forty winters shall besiege thy brow,
And dig deep trenches in thy beauty's field,
Thy youth's proud livery so gazed on now,
Will be a totter'd weed of small worth held:
Then being asked, where all thy beauty lies,
Where all the treasure of thy lusty days;
To say, within thine own deep sunken eyes,
Were an all-eating shame, and thriftless praise.
How much more praise deserv'd thy beauty's use,
If thou couldst answer 'This fair child of mine
Shall sum my count, and make my old excuse,'
Proving his beauty by succession thine!
This were to be new made when thou art old,
And see thy blood warm when thou feel'st it cold.""".split()
# build a list of tuples. Each tuple is ([word_i-2, word_i-1], target word)
trigrams = [([test_sentence[i], test_sentence[i + 1]], test_sentence[i + 2])
for i in range(len(test_sentence) - 2)]
print(trigrams[:3])
vocab = set(test_sentence)
word_to_ix = {word: i for i, word in enumerate(vocab)}
class NGramLanguageModeler(nn.Module):
def __init__(self, vocab_size, embedding_dim, context_size):
super(NGramLanguageModeler, self).__init__()
self.embeddings = nn.Embedding(vocab_size, embedding_dim)
self.linear1 = nn.Linear(context_size * embedding_dim, 128)
self.linear2 = nn.Linear(128, vocab_size)
def forward(self, inputs):
embeds = self.embeddings(inputs).view((1, -1))
out = F.relu(self.linear1(embeds))
out = self.linear2(out)
log_probs = F.log_softmax(out, dim=1)
return log_probs
losses = []
loss_function = nn.NLLLoss()
model = NGramLanguageModeler(len(vocab), EMBEDDING_DIM, CONTEXT_SIZE)
optimizer = optim.SGD(model.parameters(), lr=0.001)
for epoch in range(10):
total_loss = 0
for context, target in trigrams:
context_idxs = torch.tensor([word_to_ix[w] for w in context], dtype=torch.long)
model.zero_grad()
log_probs = model(context_idxs)
loss = loss_function(log_probs, torch.tensor([word_to_ix[target]], dtype=torch.long))
loss.backward()
optimizer.step()
total_loss += loss
losses.append(total_loss)
print(losses)输出
[(['When', 'forty'], 'winters'), (['forty', 'winters'], 'shall'), (['winters', 'shall'], 'besiege')]
[tensor(518.5248), tensor(515.9546), tensor(513.4025), tensor(510.8652), tensor(508.3428), tensor(505.8335), tensor(503.3389), tensor(500.8579), tensor(498.3887), tensor(495.9313)]
练习:计算词嵌入:Continuous Bag-of-Words
Continuous Bag-of-Words(CBOW)模型经常在NLP深度学习中使用。它基于目标单词在上下文中前面的几个单词和后面的几个单词来预测单词。这和语言模型不同,因为它不是相继连接的一个序列,也不必须计算概率。通常情况下,CBOW用于快速的训练词嵌入向量,然后拿这些向量去初始化更复杂的模型。通常,这被称为预训练嵌入。它通常会提升几个百分点的性能。
CBOW模型表述如下。给你一个目标单词![]() ,和一个N(上下文前后单词的数量)。
,和一个N(上下文前后单词的数量)。![]() ,...,
,...,![]() 和
和![]() ,...,
,...,![]() ,把上下文单词的集合称为C,CBOW试图去最小化
,把上下文单词的集合称为C,CBOW试图去最小化
其中![]() 是单词w的嵌入向量
是单词w的嵌入向量
通过对以下的class进行填空,用PyTorch来实现这个模型吧。以下是俩个建议:
- 思考下你需要定义什么参数
- 确保每个运算的形状具有合适的形状。你可以使用.view()方法来改变形状
CONTEXT_SIZE = 2 # 2 words to the left, 2 to the right
raw_text = """We are about to study the idea of a computational process.
Computational processes are abstract beings that inhabit computers.
As they evolve, processes manipulate other abstract things called data.
The evolution of a process is directed by a pattern of rules
called a program. People create programs to direct processes. In effect,
we conjure the spirits of the computer with our spells.""".split()
# By deriving a set from `raw_text`, we deduplicate the array
vocab = set(raw_text)
vocab_size = len(vocab)
word_to_ix = {word: i for i, word in enumerate(vocab)}
data = []
for i in range(2, len(raw_text) - 2):
context = [raw_text[i - 2], raw_text[i - 1],
raw_text[i + 1], raw_text[i + 2]]
target = raw_text[i]
data.append((context, target))
print(data[:5])
class CBOW(nn.Module):
def __init__(self):
pass
def forward(self, inputs):
pass
# create your model and train. here are some functions to help you make
# the data ready for use by your module
def make_context_vector(context, word_to_ix):
idxs = [word_to_ix[w] for w in context]
return torch.tensor(idxs, dtype=torch.long)
make_context_vector(data[0][0], word_to_ix) # example输出
[(['We', 'are', 'to', 'study'], 'about'), (['are', 'about', 'study', 'the'], 'to'), (['about', 'to', 'the', 'idea'], 'study'), (['to', 'study', 'idea', 'of'], 'the'), (['study', 'the', 'of', 'a'], 'idea')]
如果你不想做填空题,没有关系,下面是填好空的代码
CONTEXT_SIZE = 2 # 2 words to the left, 2 to the right
EMBEDDING_DIM=20
raw_text = """We are about to study the idea of a computational process.
Computational processes are abstract beings that inhabit computers.
As they evolve, processes manipulate other abstract things called data.
The evolution of a process is directed by a pattern of rules
called a program. People create programs to direct processes. In effect,
we conjure the spirits of the computer with our spells.""".split()
# By deriving a set from `raw_text`, we deduplicate the array
vocab = set(raw_text)
vocab_size = len(vocab)
word_to_ix = {word: i for i, word in enumerate(vocab)}
data = []
for i in range(2, len(raw_text) - 2):
context = [raw_text[i - 2], raw_text[i - 1],
raw_text[i + 1], raw_text[i + 2]]
target = raw_text[i]
data.append((context, target))
print(data[:5])
class CBOW(nn.Module):
def __init__(self,vocab_size,context_size,embedding_dim):
super(CBOW,self).__init__()
self.embeddings=nn.Embedding(vocab_size,embedding_dim)
self.linear1=nn.Linear(context_size*2*embedding_dim,256)
self.linear2=nn.Linear(256,vocab_size)
def forward(self, inputs):
embeds=self.embeddings(inputs).view(1,-1)
out=F.relu(self.linear1(embeds))
out=self.linear2(out)
out=F.log_softmax(out,dim=1)
return out
# create your model and train. here are some functions to help you make
# the data ready for use by your module
def make_context_vector(context, word_to_ix):
idxs = [word_to_ix[w] for w in context]
return torch.tensor(idxs, dtype=torch.long)
make_context_vector(data[0][0], word_to_ix) # example
losses=[]
loss_function=nn.NLLLoss()
model=CBOW(vocab_size,CONTEXT_SIZE,EMBEDDING_DIM)
optimizer=optim.SGD(model.parameters(),lr=0.001)
for epoch in range(10):
total_loss=0
for context,target in data:
context_idxs=make_context_vector(context,word_to_ix)
model.zero_grad()
log_probs1=model(context_idxs)
loss=loss_function(log_probs1,torch.tensor([word_to_ix[target]],dtype=torch.long))
total_loss += loss
loss.backward()
optimizer.step()
losses.append(total_loss)
print(losses)输出
[tensor(226.9995), tensor(224.1626), tensor(221.3551), tensor(218.5737), tensor(215.8168), tensor(213.0830), tensor(210.3716), tensor(207.6829), tensor(205.0123), tensor(202.3596)]
序列模型和LSTM(Long-Short Term Memory)网络
我们已经看到过各种的前馈网络。也就是说,这些网络中没有存储任何的状态。但有时候这并不是我们想要的。序列模型是NLP的核心:它们是输入对时间存在某种依赖关系的模型。序列模型的经典例子是隐含马尔可夫模型。另一个例子是条件随机场。
循环神经网络是指可以保存某种状态的网络。例如,它的输出可以被用作下个部分输入,以便信息可以通过序列传播。在LSTM网络中,对于序列的每一个元素,都有一个隐含状态ht,原则上该状态可以包含序列较早时刻任一点的信息。我们可以使用隐含状态来预测语言模型中的单词,词性标注及其他。
在PyTorch中使用LSTM
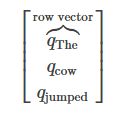
在进行例子之前,注意一些事情。PyTorch的LSTM期望所有的输入是3维的张量。理解这些张量的轴信息是很重要的。第一个轴是序列本身,第二个轴为mini-batch的索引,第三个轴是输入。我们还没讨论过mini-batching,你可以忽略它并假设第二维的值一直为1.如果我们用序列“The cow jumped”运行序列模型,我们的输入看起来像
这里不要忘记,还有值为1的第二个轴。
另外,你也可以每次只运行序列的一个元素,这样的话第一个轴的值也为1.
让我们看一下这个例子。
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)lstm=nn.LSTM(3,4)#Iput dim is 3, output dim is 4
inputs=[torch.randn(1,3) for _ in range(5)]#make a sequence of length
#initialize the hidden state
hidden=(torch.randn(1,1,4),torch.randn(1,1,4))
for i in inputs:
out,hidden=lstm(i.view(1,1,-1),hidden)
inputs=torch.cat(inputs).view(len(inputs),1,-1)
hidden=(torch.randn(1,1,4),torch.randn(1,1,4))
out,hidden=lstm(inputs,hidden)
print(out)
print(hidden)
输出
tensor([[[-0.2566, 0.1294, 0.0441, -0.5235]],
[[-0.4444, 0.0762, 0.0304, -0.3889]],
[[-0.1741, 0.1061, -0.0179, -0.1505]],
[[-0.1409, 0.1110, 0.0773, -0.2373]],
[[-0.2308, 0.1164, -0.0115, -0.2423]]])
(tensor([[[-0.2308, 0.1164, -0.0115, -0.2423]]]), tensor([[[-0.4093, 0.6065, -0.0288, -0.4107]]]))例子:使用LSTM实现词性标注
在这节,我们将使用LSTM实现词性标注。我们不会使用字节,及其前后关系,但是做为一个练习,当你看完这个例子后可以思考下是否可以使用字节信息。
模型如下所述:设我们的句子为![]() ,...,
,...,![]() ,其中
,其中![]() 属于V,即词汇表。同样,T是我们的标注集合,
属于V,即词汇表。同样,T是我们的标注集合,![]() 是单词
是单词![]() 的标注。
的标注。![]() 表示单词
表示单词![]() 的预测标注。
的预测标注。
这是一个结构预测模型。我们的输出是一个序列![]() ,...,
,...,![]() ,其中
,其中![]() 属于T。
属于T。
为了进行预测,我们需要把句子传递给LSTM。![]() 表示在时间点i上的隐藏状态。同样,为每个标注分配一个唯一索引(就像单词嵌入讲到的word_to_ix一样)。然后我们的预测规则是
表示在时间点i上的隐藏状态。同样,为每个标注分配一个唯一索引(就像单词嵌入讲到的word_to_ix一样)。然后我们的预测规则是
意思就是,预测标签是隐藏状态的仿射变换取logsoftmax的最大值。注意这表明A的目标空间的维度为|T|。
准备数据:
def prepare_sequence(seq,to_ix):
idxs=[to_ix[w] for w in seq]
return torch.tensor(idxs,dtype=torch.long)
training_data = [
("The dog ate the apple".split(), ["DET", "NN", "V", "DET", "NN"]),
("Everybody read that book".split(), ["NN", "V", "DET", "NN"])
]
word_to_ix={}
for sent,tag in training_data:
for word in sent:
if word not in word_to_ix:
word_to_ix[word]=len(word_to_ix)
print(word_to_ix)
tag_to_ix={"DET":0,"NN":1,"V":2}
EMBEDDING_DIM=6
HIDDEN_DIM=6
输出
{'Everybody': 5, 'ate': 2, 'apple': 4, 'that': 7, 'read': 6, 'dog': 1, 'book': 8, 'the': 3, 'The': 0}定义模型
class LSTMTagger(nn.Module):
def __init__(self,embedding_dim,hidden_dim,vocab_size,tagset_size):
super(LSTMTagger,self).__init__()
self.hidden_dim=hidden_dim
self.word_embeddings=nn.Embedding(vocab_size,embedding_dim)
self.lstm=nn.LSTM(embedding_dim,hidden_dim)
self.hidden2tag=nn.Linear(hidden_dim,tagset_size)
self.hidden=self.init_hidden()
def init_hidden(self):
#the axes semantics are (num_layers,minibatch_size,hidden_size)
return (torch.zeros(1,1,self.hidden_dim),
(torch.zeros(1,1,self.hidden_dim)))
def forward(self, sentence):
embeds=self.word_embeddings(sentence)
lstm_out,self.hidden=self.lstm(embeds.view(len(sentence),1,-1),self.hidden)
tag_space=self.hidden2tag(lstm_out.view(len(sentence),-1))
tag_scores=F.log_softmax(tag_space,dim=1)
return tag_scores训练模型
model=LSTMTagger(EMBEDDING_DIM,HIDDEN_DIM,len(word_to_ix),len(tag_to_ix))
loss_function=nn.NLLLoss()
optimizer=optim.SGD(model.parameters(),lr=0.1)
#before training
with torch.no_grad():
inputs=prepare_sequence(training_data[0][0],word_to_ix)
tag_scores=model(inputs)
print(tag_scores)
for epoch in range(300):
for sentence,tags in training_data:
model.zero_grad()
model.hidden=model.init_hidden()
sentence_in=prepare_sequence(sentence,word_to_ix)
targets=prepare_sequence(tags,tag_to_ix)
tag_scores=model(sentence_in)
loss=loss_function(tag_scores,targets)
loss.backward()
optimizer.step()
#after training
with torch.no_grad():
inputs=prepare_sequence(training_data[0][0],word_to_ix)
tag_scores=model(inputs)
print(tag_scores)输出
tensor([[-0.9672, -1.1054, -1.2421],
[-0.9457, -1.2572, -1.1174],
[-0.9538, -1.1928, -1.1669],
[-0.9761, -1.0899, -1.2483],
[-0.9606, -1.1283, -1.2249]])
tensor([[-0.0773, -3.7290, -2.9876],
[-5.2341, -0.0289, -3.7640],
[-2.4058, -2.8015, -0.1636],
[-0.0431, -5.0451, -3.3325],
[-5.8218, -0.0123, -4.6852]])
练习:使用字符级特征增强LSTM词性标注器
在上面的例子中,每个单词有一个嵌入向量,作为序列模型的输入。让我们使用单词的字符来增强单词的嵌入向量。我们期望这能够有很大的帮助,因为字符级的信息,比如词缀,对词性有很大的影响。例如,在英语中词缀-ly几乎总是形容词。
要做到这一点,我们使用![]() 表示单词w的字符。
表示单词w的字符。![]() 代表单词的嵌入向量。那么序列模型的输入就是
代表单词的嵌入向量。那么序列模型的输入就是![]() 和
和![]() 的连接。所以如果
的连接。所以如果![]() 有5个维度,
有5个维度,![]() 有三个维度,那么我们的LSTM的输入应该是8维的。
有三个维度,那么我们的LSTM的输入应该是8维的。
为了获得字符级别表述,对单词的字符执行LSTM模型,然后让![]() 作为LSTM的最后隐藏层的输出。提示:
作为LSTM的最后隐藏层的输出。提示:
- 在你的模型中将有两个LSTM。原来的那个输出标签分数,新的输出单词字符级表述。
- 要在字符上执行序列模型,你将使用字符嵌入。字符的嵌入向量将为字符LSTM的输入。
练习答案代码:
高级:动态决策和Bi-LSTM CRF
动态与静态深度学习工具包
PyTorch是一个动态神经网络工具包。另一个动态工具包是Dynet(我提到它因为PyTorch和Dynet很相似。如果你看到Dynet的一个例子,很可能会帮助你在PyTorch中实现它)。与之相反的是静态工具包,其中包括Theano,Keras,TensorFlow等。核心的不同如下所述:
- 在静态工具包中,你定义计算图一次,编译它,然后传递实例运行
- 在动态工具包中,你为每个实例定义一次计算图。它从不编译并在运行时执行。
经验不丰富,很难体会其中的差异。一个例子是假设我们要构建一个深层组成的解析器。假设我们的模型大致包括以下步骤:
- 自底而上构建分析树
- 标记根节点(句子的单词)
- 使用神经网络和词嵌入来寻找成分的组合。每当你形成新的成分时,使用某种技术来获得成分的嵌入。在这种情况下,我们的网络结构完全依赖于输入语句。句子“The green cat scratched the wall”,在模型的某个点上,我们想要使用组合(i,j,r)=(1,3,NP)(也就是说,一个NP,noun phrase即名词陈芬跨越单词1-单词3,在本例中是“the green cat”)
然而,另一个句子很可能是“Somewhere,the big fat cat scratched the wall”.在这个句子中,我们想要形成成分(2,4,NP)。成分的形成是依赖于输入实例的。如果我们只编译一次计算图,就像静态工具包中一样,那么对这种逻辑进行编程将非常困难或不可能。在一个动态工具包中,不只是一个预定义的计算图。每个实例都可以有一个新的计算图,所以这个问题就消失了。
动态工具箱还具有易于调试和代码更类似于宿主语言的优点(我的意思是PyTorch和Dynet比Keras和Theano看起来更像真正的Python代码)
Bi-LSTM条件随机场讨论
在本节中,你将会看到一个完整的,复杂的Bi-LSTM条件随机场(CRF,Conditional Random Field)用于命名实体识别(NER,named-entity recognition)的例子。上述LSTM标记器通常足以进行词性标注,但是对NER来说CRF序列模型N的高性能是必不可少的。假设你是熟悉CRF的。尽管名字听起来很吓人,除了使用LSTM提供特征外,所有的模型都是CRF。这是一个高级模型,比本教程中任何早期模型都要复杂。如果你想调过它学习,也是可以的。检测你是否已经准备好了,你可以:
- 写下标签k在i步维特比变量的循环
- 修改上面的循环来计算前向变量
- 再次修改上述循环来计算对数空间的前向变量(提示:log-sum-exp)
如果你可以做这三件事,你应该可以理解下面的代码。回想CRF计算条件概率。设y是标签序列,x是单词的输入序列,然后我们计算
其中Score是通过某种对数可能性![]() 来定义的
来定义的
为了使区分函数易于处理,可能性必须只考虑局部特征
在Bi-LSTM CRF中,我们只定义两种可能性:(emission probability,输出概率)和(transition probability,转换概率)。emission可能性来自Bi-LSTM在时间i处的隐藏状态,transition scores存储在|T|x|T|矩阵P中,其中T是标注集合。在我的实现中,![]() 是标签j转移到标签k的概率。所以:
是标签j转移到标签k的概率。所以:
在第二个表达式中,我们认为标签是非负唯一的。
如果以上的讨论太过简洁,你可以通过查看Michael Collins写的CRFs。
实现注意事项
以下的例子实现了前馈算法
练习:判别标注的一种新的损失函数
是