机器学习算法之 决策树 decision tree
决策树 decision tree
算法原理:
构造一个决策树,即通过特征构造一个树,如下图。沿着树结构访问树节点直到得到数据的分类结果。构造树时先找出一个决定性
的特征,这个特征把数据分为几个数据子集,即分支节点,如果分支节点的数据全部属于同一类,那么这个分类已结束,否则再进步分
类。找出这个最佳(决定性的)特征很重要,
香浓熵(也叫信息熵),表示混杂程度,香浓熵越高混杂程度越高(比如,一个罐子里两种硬币,其中一种硬币占绝大多数,这个叫
纯度高,即混杂度低,香浓熵低)。香浓熵:
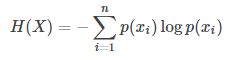
其中p(Xi)为x取i分类的概率值。
换个角度说,混杂度越高变量的不确定性越大,熵也就越大,把它搞清楚所需要的信息量也就越大。所以我们找到一个特征尽量
把数据分的纯度高点,比如分类目标为A、B,特征1进行分类90%为A类10%位B,特征2进行分类40%为A类60%为B类,那么特征1
的信息增益高(香浓熵底),选择特征1。
如上图,我们使用决策树算法,先构造这个决策树:
1、找到最佳数据划分方式,最大增益即香浓熵最小的特征,按特征建立树的两个子树(子节点)
2、子树按第一步骤递归建立树
预测算法
遍历决策树,直到叶子节点
决策树算法优劣:
优点:计算复杂度不高,输出结果易于理解,对中间值不明感,可以处理不相关的特征值
缺点:可能产生过度分类问题
代码:
计算香浓熵:
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet: #the the number of unique elements and their occurance
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
#print(labelCounts)
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob * log(prob,2) #log base 2
return shannonEnt
#构造一个测试数据
def createDataSet():
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing','flippers']
#change to discrete values
return dataSet, labels
测试
>>> import trees
>>> myData,labels = trees.createDataSet()
>>> myData
[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
>>> trees.calcShannonEnt(myData)
0.9709505944546686
