AlphaGo Zero强化学习简易教程(译)
本教程介绍了一个同步的单线程单GPU的game-agnostic的AlphaZero复现工作。这是一部很漂亮的作品,它训练了一个仅通过自己和自己下棋的方式来学习的智能体,除了游戏规则之外,智能体没有利用任何的人类知识。与DeepMind之前的论文相比,该方法相当简单,而且AlphaGo Zero最终令人信服地击败了AlphaGo。AlphaGo使用专家游戏的数据进行训练,并击败了最好的人类围棋选手。最近,DeepMind在Arxiv上发布了AlphaZero的预印版,将AlphaGo Zero方法扩展到国际象棋和日本将棋。
这篇文章的目的是从AlphaGo Zero论文中提炼出关键思想,并通过代码具体地理解它们。我们假定读者基本熟悉机器学习和强化学习概念,如果您了解神经网络基础知识和蒙特卡洛树搜索,则应该可以更容易理解。在开始之前(或者在读完本教程之后),我建议阅读原始论文。它写得很好,可读性很强,插图也很漂亮!AlphaGo Zero是通过自我游戏(self-play)强化学习来训练的。它将神经网络和蒙特卡罗树搜索结合在一个优雅的策略迭代框架中,实现了稳定的学习。不过,这只是空话-让我们立即深入研究细节吧!
神经网络
毫不意外的是,AlphaGo Zero的核心是一个神经网络。网络 f θ f_\theta fθ( θ \theta θ是神经网络的权重)以棋盘的某个状态作为输入。网络有两个输出:
- v θ ( s ) ∈ [ − 1 , 1 ] v_\theta(s) \in [-1,1] vθ(s)∈[−1,1], 受棋盘状态 s s s控制的连续值,实则为当前玩家视角的状态值函数 V π ( s ) V_\pi(s) Vπ(s)。
- p θ ( s ) p_\theta(s) pθ(s), 指示了动作空间中所有动作可能采取的概率值,即策略 π ( a ∣ s ) \pi(a|s) π(a∣s)
在训练神经网络时,我们在每盘棋结束时向模型送入训练数据,数据格式如 ( s t , π t , z t ) (s_t,\pi_t,z_t) (st,πt,zt), π t \pi_t πt是从当前状态 s t s_t st估计的策略向量(下一节我们介绍如何从一个状态估计策略), z t ∈ { − 1 , 1 } z_t \in \{ -1,1\} zt∈{−1,1}是当前玩家视角在状态 s t s_t st时对游戏输赢的估计值,+1表示当前玩家赢得棋局,-1表示输掉。(为什么总是强调当前玩家视角,AlphaGo Zero采取左右手互博的机制,在某一回合执白棋,下一回合则执黑棋,黑白双方对棋局的预测是截然相反的,零和游戏嘛) 网络的优化函数如下所示,不包括正则化项。
l = ∑ t ( v θ ( s t ) − z t ) 2 − π t ⋅ log ( p θ ( s t ) ) l=\sum_t (v_\theta(s_t)-z_t)^2-\pi_t \cdot \log(p_\theta(s_t)) l=t∑(vθ(st)−zt)2−πt⋅log(pθ(st))
这样训练的内在含义就是,希望经过训练,网络可以最终学到哪些状态可能导致最终的胜利,哪些状态可能导致最后的失败。另外,对策略的学习将会使网络对何时采取何种动作给出一个较好的估计。网络结构取决于不同的游戏,大部分棋类游戏比如围棋可以采用多层的卷积神经网络。在Deepmind论文中,作者采用了20个残差模块(residual blocks),每个block有两个卷积层。对于 6 × 6 6\times6 6×6棋盘的黑白棋游戏,我采用了四层卷积层+若干全连接层的方式来学习。
用蒙特卡洛树搜索进行策略优化
给定一个状态 s s s(在围棋中就是若干个黑棋白棋分布在 19 × 19 19\times19 19×19的棋盘上),神经网络就可以根据这个状态估计一个策略向量 p θ ( s ) p_\theta(s) pθ(s)。我们希望在训练过程中能够优化对策略函数的估计(预测)能力。论文中,完成这一任务的是蒙特卡洛树搜索(Monte Carlo Tree Search,MCTS)。在搜索树中,每个节点代表一个棋盘状态,一条有向边 i → j i \rightarrow j i→j代表存在一个合乎游戏规则的动作可以使状态 i i i 转移到状态 j j j 。搜索从一颗空的树开始,一次添加一个结点。当一个新节点被添加到树的末端,并不会马上继续向下拓展,而是先由神经网络计算出这个结点的值。这个值将会沿着树的搜索路径传播下去。详细的算法解释如下。
对于树搜索,我们需要以下数据:
- Q ( s , a ) Q(s,a) Q(s,a): 在状态 s s s采取动作 a a a的期望回报,也就是Q值函数;
- N ( s , a ) N(s,a) N(s,a): 整个蒙特卡洛模拟过程中,在状态 s s s采取动作 a a a的次数;
- P ( s , ⋅ ) = p θ ( s ) P(s,\cdot)=p_\theta(s) P(s,⋅)=pθ(s): 利用当前神经网络估计的策略计算的,在状态 s s s可能采取动作的概率。
当有了以上数据,我们就可以计算 U ( s , a ) U(s,a) U(s,a), 即Q值的上限置信区间
U ( s , a ) = Q ( s , a ) + c p u c t ⋅ P ( s , a ) ⋅ ∑ b N ( s , b ) 1 + N ( s , a ) U(s,a)=Q(s,a)+c_{puct} \cdot P(s,a) \cdot \frac{\sqrt{\sum_b N(s,b)}}{1+N(s,a)} U(s,a)=Q(s,a)+cpuct⋅P(s,a)⋅1+N(s,a)∑bN(s,b)
上式中, c p u c t c_{puct} cpuct是控制探索(exploration)程度的超参数。如果 N ( s , a ) N(s,a) N(s,a)很小,意味着在状态 s s s很少采取动作 a a a,那么算法就会倾向于探索一下这种方案。
为了用MTCS优化当前神经网络返回的策略估计,我们首先以根节点状态 s s s初始化一个空搜索树,然后执行一步模拟操作。计算使得上限置信区间 U ( s , a ) U(s,a) U(s,a)最大的动作 a a a。如果下一个状态 s ′ s' s′(通过在状态 s s s执行动作 a a a得到的)在树中存在,就移动到结点 s ′ s' s′继续搜索;如果树中没有状态 s ′ s' s′,就将其加入搜索树,并用网络估计一个策略向量 P ( s ′ , ⋅ ) = p θ ( s ′ ) P(s',\cdot)=p_\theta(s') P(s′,⋅)=pθ(s′)和状态值函数 v ( s ′ ) = v θ ( s ′ ) v(s')=v_\theta(s') v(s′)=vθ(s′), 最后所有动作 a a a将 Q ( s ′ , a ) Q(s',a) Q(s′,a)和 N ( s ′ , a ) N(s',a) N(s′,a)都置0。当加入一个新节点之后,并不会马上继续拓展树的结构,而是将 s ′ s' s′的值沿着已知路径向 s s s方向传播,也就是用 v ( s ′ ) v(s') v(s′)更新所有的 Q ( s , a ) Q(s,a) Q(s,a) (我理解的是根据强化学习中的Q和V的关系公式来更新Q值)。另一方面,如果模拟到了终点状态,即游戏结束,我们就将真实的游戏反馈(-1或+1)反向传播回去。
经过若干轮MC模拟过程,根结点的 N ( s , a ) N(s,a) N(s,a)值将会更好地模拟一个策略。(PS:这里, N ( s , a ) N(s,a) N(s,a)实际上就是利用大量的玩游戏,确定出在某一个状态 s s s下采取各个动作的频率,用来模拟策略的概率,也就是蒙特卡洛模拟思想的本质。)优化的随机策略可以简单地用归一化的频数来确定,也就是
π ( ⋅ ∣ s ) = N ( s , ⋅ ) ∑ b N ( s , b ) \pi(\cdot|s)=\frac{N(s,\cdot)}{\sum_b N(s,b)} π(⋅∣s)=∑bN(s,b)N(s,⋅)
在self-play中,我们执行MTCS并从优化过的随机策略 π ( a ∣ s ) \pi(a|s) π(a∣s)中采样一个动作来执行。如下是树搜索的一步模拟的伪代码。
def search(s, game, nnet):
if game.gameEnded(s): return -game.gameReward(s)
if s not in visited:
visited.add(s)
P[s], v = nnet.predict(s)
return -v
max_u, best_a = -float("inf"), -1
for a in range(game.getValidActions(s)):
u = Q[s][a] + c_puct*P[s][a]*sqrt(sum(N[s]))/(1+N[s][a])
if u>max_u:
max_u = u
best_a = a
a = best_a
sp = game.nextState(s, a)
v = search(sp, game, nnet)
Q[s][a] = (N[s][a]*Q[s][a] + v)/(N[s][a]+1)
N[s][a] += 1
return -v
注意,伪代码中第二行返回的是负的状态值,这是因为树中的交替层级上的状态值是从黑白棋双方的不同视角下得到的。因为 v ∈ [ − 1 , 1 ] v\in[-1,1] v∈[−1,1], − v -v −v就是另一个玩家视角下的当前棋盘状态值。
通过自对弈(self-play)进行策略迭代
我们现在具备了无监督训练智能体的所有要素。通过自对弈进行学习本质上是一个策略迭代算法——玩游戏,利用当前策略更新Q值,然后利用大量的统计数据更新游戏策略。
如下是一个完整训练算法。我们用随机权重初始化神经网络,以一个随机策略和随机值函数开始游戏。在每次的策略迭代中,都要执行若干盘的自对弈游戏;在每盘游戏中,我们从当前状态 s t s_t st开始,执行固定次数的MCTS模拟。然后在更新过的随机策略 π t \pi_t πt 中采样一个动作,执行动作,这样我们就得到一个训练样本 ( s t , π t , _ ) (s_t,\pi_t,\_) (st,πt,_)。状态的回报 _ \_ _将会在游戏结束后填上。同样的,当前玩家赢了就填+1,输了填-1。
迭代结束后,神经网络就用采样样本进行训练。更新前后的网络将进行比拼,如果新网络能赢得一定比例的棋局(在deepmind论文中,新网络需要赢得55%的比赛),就采用新网络,否则放弃这次更新的权值。伪代码如下。
def policyIterSP(game):
nnet = initNNet() # initialise random neural network
examples = []
for i in range(numIters):
for e in range(numEps):
examples += executeEpisode(game, nnet) # collect examples from this game
new_nnet = trainNNet(examples)
frac_win = pit(new_nnet, nnet) # compare new net with previous net
if frac_win > threshold:
nnet = new_nnet # replace with new net
return nnet
def executeEpisode(game, nnet):
examples = []
s = game.startState()
mcts = MCTS() # initialise search tree
while True:
for _ in range(numMCTSSims):
mcts.search(s, game, nnet)
examples.append([s, mcts.pi(s), None]) # rewards can not be determined yet
a = random.choice(len(mcts.pi(s)), p=mcts.pi(s)) # sample action from improved policy
s = game.nextState(s,a)
if game.gameEnded(s):
examples = assignRewards(examples, game.gameReward(s))
return examples
黑白棋实验
我们在黑白棋上进行了学习实验。实验采用 6 × 6 6\times6 6×6棋盘,单GPU,每次迭代包括100盘自对弈棋局,每次MCTS执行25次仿真操作(可能是下25步棋吧)。这个计算规模相比于AlphaGo Zero小了好几个数量级。AlphaGo Zero每轮迭代下25000盘棋,每次树搜索执行1600次仿真操作。黑白棋实验用一张K80GPU跑了三天80次迭代。效果要优于一般的基准算法和人类水平。
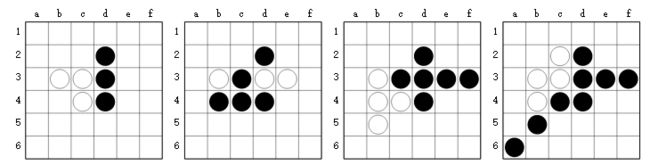
在学习过程的早期,黑棋学到了利用墙和角的优势。

The agent (Black) learns to force passes in the late game
其他细节Tips
这个tutorial介绍了AlphaGo Zero的核心思想,但是为了清晰起见,略去了一些细节如下:
- 历史状态:因为围棋从当前状态来看,不是完全可见的(since Go isn’t completely observable from the current state of the board,不是很懂这句话什么意思),所以神经网络将当前状态的前七回合也作为网络的输入。这只是围棋的特征,其他棋类如象棋和黑白棋不需要这样的操作,只需要当前棋局作为网络的输入。
- 温度:在执行MCTS之后得到的随机策略是一个树结点访问次数的幂函数(exponentiated counts),即 π ( s ) = N ( s , ⋅ ) 1 / τ ∑ b ( N ( s , b ) 1 / τ ) \pi(s)=\frac{N(s,\cdot)^{1/\tau}}{\sum_b(N(s,b)^{1/\tau})} π(s)=∑b(N(s,b)1/τ)N(s,⋅)1/τ。式中, τ \tau τ是温度参数,控制算法探索的程度。AlphaGo Zero采用 τ = 1 \tau=1 τ=1作为棋局前三十回合的温度参数,也就是动作概率 π ( s ) \pi(s) π(s)等于对动作归一化后的结点访问次数(如状态 s s s有3个可选action,整个模拟过程分别访问a1,a2,a3各100,50,20次,则采取动作a1的概率为 100 / ( 100 + 50 + 20 ) = 10 / 17 100/(100+50+20)=10/17 100/(100+50+20)=10/17);30回合之后, τ \tau τ设为无穷小,即,取访问次数最多的一个action为状态s的策略。
- 对称性:围棋的棋盘具有旋转不变性和对称不变性。当MCTS到达棋局终点时,当前神经网络输入是一个经过旋转或对称变换的棋盘,用以训练网络探索棋盘的对称性。这个技术也可以被用于其他具有对称性的棋类游戏中。
- 异步MCTS:AlphaGo Zero采用了一种异步MCTS算法,并行地进行仿真。The neural network queries are batched and each search thread is locked until evaluation completes.另外,三个主要过程:自对弈、网络训练和新旧网络对比 的计算,都是并行的。
- 计算力:每个神经网络用64块GPU和19块CPU训练,但是文中并没有给出用于自对弈的计算资源的规模。
- 神经网络结构设计:论文作者尝试了多种网络结构,包含残差结构和不包含残差结构的网络,价值网络和策略网络分享或不分享权值的网络。最优秀的网络结构是具有残差结构且policy net与value net之间共享权值的网络结构。
代码实现
https://github.com/suragnair/alpha-zero-general