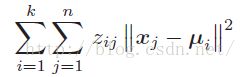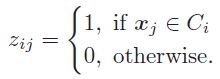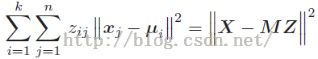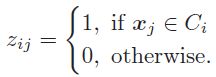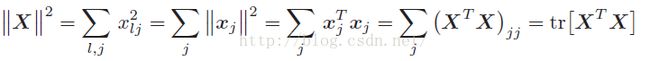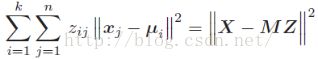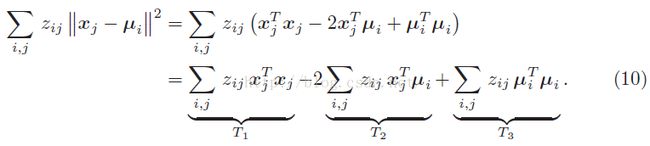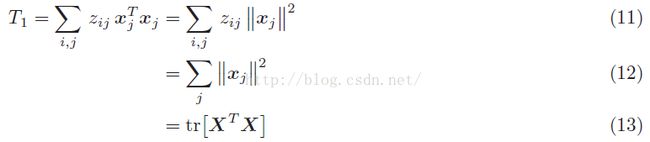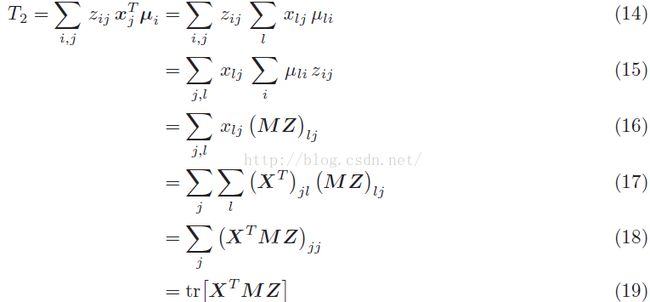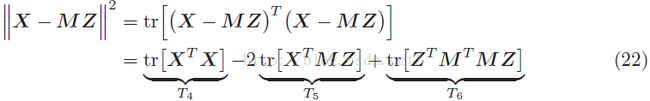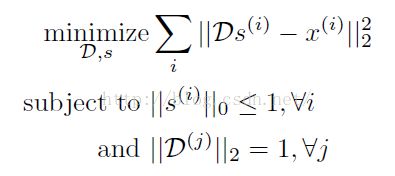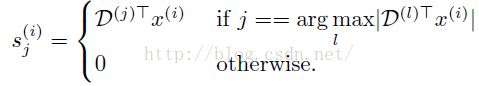深度学习（二十四）矩阵分解之基于k-means的特征表达学习

矩阵分解之基于k-means的特征表达学习

原文地址：http://blog.csdn.net/hjimce/article/details/50429317

作者：hjimce

一、相关理论

     因为最近搞的项目，要么没有数据、要么训练数据很少，精度老是提高不上去，另一方面最近看到网上一篇推荐文章:《Convolutional Clustering for Unsupervised Learning》，于是就操起家伙，学习CNN无监督学习方面的文章，看能不能把精度提高上去。

   本篇博文主要讲解2012年大神吴恩达他们曾发表的一篇paper:《Learning Feature Representations with K-means》。可能大家对于k均值聚类，这个算法之前已经非常熟悉了，觉得这个算法是一个很简单的算法，估计会觉得没什么可以学的东西，因此对其不感兴趣。然而其实很多人只是表层理解的k-means算法，对于k-means怎么用于图片分类无监督特征表达学习、k-means与矩阵分解的关系、与压缩感知相关理论之间的关系，却极少有人去深究理解。曾经的我，看到这篇文献题目的时候，曾心想:“这种文献肯定很水，连k-means这种算法也好意思拿出来发表文章”。好吧，这也许就是所谓的：坐井观天，惭愧啊。人生只有意识到自己是菜鸟的时候，才会去努力，才会进步。

   本篇博文我将从k-means与矩阵分解开始讲起，矩阵分解推导部分主要参看文献：《k-Means Clustering Is Matrix Factorization》，对公式的推导过程不感兴趣的可以跳过，个人感觉推导公式枯燥乏味。矩阵分解部分是为了对k-means有进一步的了解。因为后面要讲的特征表达学习，文献给出的公式也是一个矩阵分解的公式。第三部分，我们将详细讲解文献：《Learning Feature Representations with K-means》，深入学习如何利用k-means算法进行图片特征学习，并提高图片分类的精度，领略k-means的牛逼之处。

二、k-means与矩阵分解

这几天刚好看到这篇paper：《k-Means Clustering Is Matrix Factorization》，因此就用这篇文献进行思路讲解。最近突然领悟到矩阵分解威力好强大，好多机器学习的算法都根源于矩阵分解，如PCA、NMF、ICA、LDA、稀疏编码等，所以就决定对矩阵分解的奥义做一个总结，决定写一个系列博文，做一个总结，不然算法一多，就会乱掉。下面的的讲解，主要翻译自文献：《k-Means Clustering Is Matrix Factorization》。

1、k-means算法回顾

k均值算法可以说是机器学习中，最常用的一个聚类算法，给定数据集X∈Rm，我们的目的就是把它们分成C1，C2……CK，其中k就是我们要聚类的个数。我们知道k-means算法的原理就是最小化下面的函数：

 

其中，xj是每一个数据点，ui是聚类中心，当xj聚类为Ci时，那么zij的值就是1，如果不是那么就是为0，即：

 

2、证明

（1）证明题目

开始前我们先明确一下我们的目标，我们的目标是证明k-means的目标函数可以被分解成如下矩阵形式：

 

其中，X是数据样本矩阵，每一列表示一个样本。M是聚类中心矩阵，它的每一列就是我们的聚类中心ui，Z表示一个编码矢量：

 

就像上初中的时候，考试考证明题一样，我们的目标就是要证明上面的等式成立。也就是k-means的过程就相当于矩阵分解的过程。如果对证明过程不感兴趣的可以跳过，因为证明过程确实是挺枯燥的。而且这也不是本篇博文的重点，这只是为了让大家先对k-means的求解其实是可一个归结为一个矩阵分解问题的。

(2)定义

为了后面推导方便起见，我们先对一些代号，做一下定义。我们定义：数据样本矩阵X，X的每一列表示一个样本xj，我们把矩阵X的L2范数定义为所有样本向量的长度平方和，即：

 

OK,啰嗦了这么多，我们要大干一场了，下面开始证明等式：

 

成立。

(3)证明成立

我们先把等式左边展开：

 

然后上面的T1、T2、T3项我们可以进一步化简为：

 

 

我们把等式右边也展开：

 

这个时候，我们可以看到T4=T1，T2=T5。因此接着我们只需要证明:T3=T6，证明过程如下：

T6项等价于：

据此，我们可以进一步推导：

 

其中Z*Z^T是一个对角矩阵。至此T3=T6证明成立，因此我们最后所要证明的等式也就成立了，证毕。

啰嗦了这么多，无非就是想要说一句话：k-means也是一个矩阵分解的求解过程。

三、特征表达学习

    OK，言归正传，前面啰嗦了一大堆，仅仅只是为了说明一个问题：k-means的求解过程是一个矩阵分解的过程。本部分要讲的利用k-means做特征学习，才是我们要关注的东西。接着我们要讲的东西就是文献：《Learning Feature Representations with K-means》到底是怎么实现无监督特征学习。本部分同时也参考了前辈zouxy的博文：http://blog.csdn.net/zouxy09/article/details/9982495 ，感谢前辈。

    开始前先要讲一下spherical K-means算法，这个算法与我们平时学到的k-means算法稍微有点不同，是k—means算法的一个进化版。所以需要先熟悉一下这个算法。spherical K-means故名思议，意思应该是我们的数据点集全部分布在一个球面上，然后进行聚类。因此在采用这个算法的时候，需要对每个数据点归一化处理，使得我们要聚类的数据，分布在一个球面上，然后我的个人理解这一个球面聚类，应该是用了余弦相似度度量替代了欧式距离度量（具体没有细看，只是个人浅薄理解，可能有误）。

1、字典与矢量量化

首先文献采用的k—means算法是：spherical K-means，其满足如下条件：

 

其中，D我们由称之为字典，字典这个词把我难住了，我不是信息专业的，从没听过字典，好高大上的名字。然而其实说白了D就是一个变换矩阵。D(j)就是表示D的第j每一列，D的每一列就是我们k均值的聚类中心向量，因为我们的聚类是在单位球面上，所以聚类中心的模长等于1。

S又称之为特征向量编码，当D的第j列（聚类中心）与x(i)最近的时候，s(i)对应的元素不为0，其余全部为0。这个就是对x(i)的一个编号罢了，比如我们对X进行聚类，聚类为5个类，最后如果xi被聚类为第3个类别，那么编码矢量si=（0,0,1,0,0）。编码这个词听起来好像也有点牛逼的样子，其实我们也可以把s理解为特征。而k-means特征提取的过程，说白了就是计算s。

   K-mean无监督学习的过程，说白了就是为了学习字典D，也就是每个聚类中心。然后当我们输入一个新数据x的时候，我们就用D去计算S，计算公式如下：

 

简单理解一下上面的那个符号：argmax。因为我们是在一个球面上，两点间如果最近，那么Dj*Xi应该是最大的(点积、余弦)。

2、算法流程

至今为止，我们都还没扯到图像，扯到图像的特征学习，接着我们就要开始结合实际应用，讲诉k-means的特征学习过程。

（1）数据获取

对于图像，我们要如何进行k-means无监督特征学习？我们从一堆的图片中，随机的抽取出一大堆的图片块（16*16大小的块），然后把这些16*16的图片块（这个是灰度图），拉成一个一维的向量xi，也就是256维的特征向量，这就是我们的训练数据了。文献抽取出了100000个16*16的图片块，进行字典学习。

（2）数据预处理

a、亮度和对比度归一化。采用如下公式对样本xi进行归一化：

 

这个简单，搞过机器学习的人都知道，上面公式分母加了一个数：10，是为了避免除数是0。

b、白化

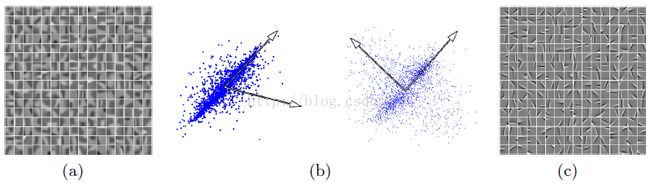
这个我们可以采用PCA白化也可以采用ZCA白化，不过我们需要注意的是：白化的过程对于我们的结果非常重要，所以千万不要忘了白化。这个文献对是否采用白化进行了对比：

 

左边是没用使用白化，聚类出来的中心。右边则是我们采用白化，学习得到的字典。

(3)最后就是spherical k-means的聚类过程了。

最后算法总流程如下：

3、图片识别应用

前面我们介绍了，给定一堆无标签图片，我们通过K-means算法，进行学习字典D。接着我们就要知道它具体是怎么用于图片识别分类的。下面是算法的总流程：

(1)通过无监督学习，学习到一系列的字典D。

(2)接着我们利用学习到的字典，把一张输入图片，进行函数映射：

我们可以把这个过程看成是卷积，比较容易理解。这个映射过程不一定是非重叠的。

(3)采用pooling进行降维。

(4)如果是构建多层网络，那么就重复上面的过程。如果单层网络，那么我们就后面接一个分类器，比如svm。

后面就不再细讲了，个人感觉：http://blog.csdn.net/zouxy09/article/details/9982495 讲的很好，觉得自己再怎么细讲，也没有前辈讲的很细，自叹不如啊，所以本篇博文到此结束。

参考文献：

1、《k-Means Clustering Is Matrix Factorization》

2、《Learning Feature Representations with K-means》

3、http://blog.csdn.net/zouxy09/article/details/9982495 

4、《An Analysis of Single-Layer Networks in Unsupervised Feature Learning》

5、《Convolutional Clustering for Unsupervised Learning》

**********************作者：hjimce   时间：2015.12.12  联系QQ：1393852684    原创文章，转载请保留原文地址、作者等信息***************